Quantum Mechanics (QM) derived from Special Relativity (SR)
The RoadMap to the SRQM Interpretation of Quantum Mechanics
A Study of Physical 4-Vectors, Tensors, and Lorentz Invariants

A physical derivation of Quantum Mechanics (QM) using only the assumptions of Special Relativity (SR) as a starting point...
Quantum Mechanics is not only totally compatible with Special Relativity, QM is derivable from SR.
This is the "SRQM Interpretation of Quantum Mechanics", or alternately, the "[SR→QM] Interpretation of Quantum Mechanics",
as well as a Study of Physical 4-Vectors, Tensors, and Lorentz Invariants.
A treatise by John B. Wilson.


SiteMap of SciRealm \| About John \| John's Resume/C.V./Bio \| Send email to John John's Science, Math, Philosophy Stuff: The Science Realm: John's Virtual Sci-Tech Universe \| 4-Vectors \| Ambigrams \| Antipodes \| Covert Ops Fragments \| Cyrillic Projector \| Forced Induction (Sums Of Powers Of Integers) \| Fractal Tree \| Frontiers \| IFS Fractals (Assembly) \| IFS Fractals (Javascript) \| JavaScript Graphics \| Kid Science \| Kryptos \| Philosophy \| Photography \| Physics-Planck Constant Measurement Via LEDs \| Prime Sieve \| QM from SR \| QM from SR-Simple RoadMap \| QM from SR-Simple RoadMap (PDF) \| SR 4-Vector & Tensor Calculator \|Quantum Phase \| Quotes \| RuneQuest Cipher Challenge \| Secret Codes & Ciphers \| Scientific Calculator (complex capable) \| Science+Math \| Sci-Pan Pantheist Poems \| Stereograms \| SuperMagicSqr4x4 \|Turkish Grammar \|Melike Wilson Art Site last modified: 2023	Welcome to Relativistic Quantum Reality: Virtual worlds of imaginary particles: The dreams stuff is made of: Life, the eternal ghost in the machine... This site is dedicated to the quest for knowledge and wisdom, through science, mathematics, philosophy, invention, and technology. May the treasures buried herein spark the fires of imagination like the twinkling jewels of celestial light crowning the midnight sky... Quantum Mechanics is derivable from Special Relativity See SRQM - QM from SR - Simple RoadMap (.html) See SRQM - QM from SR - Simple RoadMap (.pdf) See SRQM - QM from SR - Summary (.pdf) See SRQM - Fundamental Constants (.pdf) See SRQM - Online SR 4-Vector & Tensor Calculator See Online Complex-capable RPN Scientific Calculator *Learn, Discover, Explore*

Both General Relativity (GR) and Special Relativity (SR) have passed very stringent tests of multiple varieties.
Likewise, Relativistic Quantum Mechanics (RQM) and standard Quantum Mechanics (QM) have passed all tests within their realms of validity:
{ generally micro-scale systems: ex. Single particles, ions, atoms, molecules, electric circuits, atomic-force microscopes, etc.,
but a few special macro-scale systems: ex. Bose-Einstein condensates, super-currents, super-fluids, long-distance entanglement, etc.}.

To-date, however, there is no observational/experimental indication that quantum effects "alter" the fundamentals of either SR or GR.
Likewise, there are no known violations, QM or otherwise, of Local Lorentz Invariance (LLI) nor of Local Position/Poincaré Invariance (LPI).
In fact, in all known experiments where both SR/GR and QM are present, QM respects the principles of SR/GR, whereas SR/GR modify the results of QM.
All tested quantum-level particles, atoms, isotopes, super-positions, spin-states, etc.
obey GR's Universality of Free-Fall & Equivalence Principle and SR's{ E = mc² } and speed-of-light (c) communication/signaling limit.
Meanwhile, quantum-level atomic clocks are used to measure gravitational red:blue-shift effects.
i.e. GR gravitational frequency-shift (gravity time-dilation) alters atomic=quantum-level timing.

Think about that for a moment...

Some might argue that QM modifies the results of SR, such as via non-commuting measurements.
However, that is an alteration of CM expectations,not SR expectations.
In fact, there is a basic non-zero commutation relation fully within SR:( [∂^μ,X^ν] = η^μν ) which will be derived from purely SR Principles.
The actual commutation part ( Commutator [a,b] ) is not about ( ћ ) or ( i ), which are just Lorentz invariant multipliers.

On the other hand, GR Gravity *does* induce changes in quantum interference patterns and hence modifies QM:
See the COW gravity-induced neutron QM interference experiments,
the LIGO & VIRGO & (soon) KAGRA gravitational-wave detections via QM interferometry,
and now also QM atomic matter-wave gravimeters via QM interferometry.

Likewise, SR induces fine-structure splitting of spectral lines of atoms, “quantum” spin, spin magnetic moments, spin-statistics (fermions & bosons),
antimatter, QED, Lamb shift, relativistic heavy-atom effects (liquid mercury, yellowish color of gold,
lead batteries having higher voltage than classically predicted, heavy noble-gas interactions, relativistic chemistry...), etc.
- essentially requiring QM to be RQM to be valid.
QM is instead seen to be the limiting-case of RQM for { |v| << c }.

Some QM scientists say that quantum entanglement is "non-local", but you still can't send any real messages/signals/information/particles faster than SR's speed-of-light (c).
The only “non-local” aspect is the alteration of probability-distributions based on knowledge-changes obtained via measurement.
A local measurement can only alter the “partial information” already-known about the probability-distribution of a distant (entangled) system.
There is no FTL-communication-with nor alteration-of the distant particle.
Getting a Stern-Gerlach “up” here doesn’t cause the distant entangled particle to suddenly start moving “down” there.
One only knows “now” that it “would” go down “if” the distant experimenter actually performs the measurement.

Again, QM respects the principles of SR/GR, whereas SR/GR modify the results of QM.

The following is a derivation of Relativistic Quantum Mechanics (RQM) and Quantum Mechanics (QM) from Special Relativity (SR).
It basically highlights the few extra physical assumptions necessary to generate QM given SR as the base assumption.
The Axioms of QM are not required, they emerge instead as Principles of QM based on SR derivations.
This is the "SRQM Interpretation of Quantum Mechanics", or alternately, the "[SR→QM] Interpretation of Quantum Mechanics",
as well as a Study of Physical 4-Vectors, Tensors, and Lorentz Invariants.
A treatise by John B. Wilson.

=============================

QM is the low-velocity limiting-case { |v| << c }of RQM, which is itself completely contained within the principles of SR.
SR is itself simply the low-mass limiting-case { g^μν → η^μν } of GR. Hence, QM is contained within the Axioms of GR.
We should not be looking to "Quantize Gravity", we should be looking to "General Relativize Quantum Mechanics".
In short: QM is *NOT* fundamental. GR so far appears to be fundamental.

Thus, this treatise explains the following:
Why GR works so well in its realm of applicability {large scale systems}.
Why QM works so well in its realm of applicability {micro scale systems and certain macroscopic systems}.
i.e. The tangent space to any GR curvature is locally Minkowskian, and thus QM works for small volumes...
Why RQM explains more stuff than QM without SR.
Why all attempts to "quantize gravity" have failed {essentially, everyone has been trying to put the cart (QM) before the horse (GR)}.
Why all attempts to modify GR keep conflicting with experimental data {because GR is apparently fundamental}.
Why QM works perfectly well with SR as RQM but not with GR {because QM is derivable from SR, hence a manifestation of SR rules}.
How Minkowski Space, 4-Vectors, and Lorentz Invariants play vital roles in RQM, and give the SRQM Interpretation of Quantum Mechanics.

Major clues:
RQM describes and explains phenomena that standard QM cannot.
Mass **and** Spin are Casimir Invariants of Poincaré Invariance, which comes from SR Minkowski space, not QM.
Hence, spin does not require a quantum axiom for its existence.
To date, there have been no repeatable violations of either Poincaré or Lorentz Invariance, nor of Local Position Invariance, which rule out many alternative gravity theories.
The main Schrödinger relation is just a special case of plane waves on objects (4-Vectors) already connected in standard SR.
All connections between SR 4-Vectors are Lorentz Invariants, with, to date, no evidence of change over time during the age of the universe.
CM can be done with a Hilbert Space description: see Koopman-von Neumann Classical Mechanics.
QM can be done without a Hilbert Space description: see Phase Space Formulation of Quantum Mechanics.
Hence, Hilbert space does not require a quantum axiom for its existence.
Particles of CM and QM can be described by a wave theory: see Hamilton-Jacobi Equations.
Measurement of Planck's constant can be done with experiments that do not need quantum theory to explain, just standard SR.
50+ years of unsuccessful attempts to "quantize gravity".
To date, no new particles found outside of the Standard Model by LHC or other experiments.

=============================

Other sources:
PDF slideshow presentation: SRQM.pdf
Open/LibreOffice Presentation SRQM.odp
Alternate discussion at SRQM.html
SRQM Flyer: SRQM_Flyer.pdf, SRQM_Flyer.odt
See 4-Vectors & Lorentz Scalars Reference for more info on Four-Vectors (4-Vectors) in general
See John's Online RPN Scientific Calculator, using Complex Math
See SRQM - Online SR 4-Vector & Tensor Calculator

Physics-PlanckConstantViaAtomicLineSpectra.html
Physics-PlanckConstantViaComptonScattering.html
Physics-PlanckConstantViaElectronDiffraction.html
Physics-PlanckConstantViaGravityInducedInterferometry
Physics-PlanckConstantViaIncandescence.html
Physics-PlanckConstantViaLEDs.html
Physics-PlanckConstantViaSagnacEffect.html
Physics-PlanckConstantViaSternGerlach.html

SRQM 4-Vectors and Lorentz Scalars

SRQM 4-Vector and Lorentz Scalar Diagram

SRQM Physics Diagramming Method

Where do we start?
First:
I will show the really short version, the Roadmap from SR to QM...
Then:
I will begin with some basic assumptions and background stuff on Special Relativity (SR), Lorentz Scalars, 4-Vectors, and Tensors.
I will introduce the SR Physical 4-Vectors, which encapsulate the Physical Properties of Nature.
I will show how these SR 4-Vectors are related to one another in purely relativistic theory, i.e. the Physical Laws of Nature.
I will show a couple of relations that have previously been considered quantum assumptions/axioms/postulates,
but which are, in fact, fundamentally no different from the other SR relations.
I will derive relativistic quantum wave equations based just on these few SR relations.
I will derive the principles of Quantum Mechanics (QM), assuming no axioms of QM.

Roadmap from Special Relativity to Quantum Mechanics: (The Short Version)

Start with a few SR Physical 4-Vectors:
4-Position R = (ct,r)
4-Velocity U = γ(c,u)
4-Momentum P = (E/c,p) = (mc,p)
4-WaveVector K = (ω/c,k)
4-Gradient ∂ = (∂_t/c,-∇)

Note the following relations between SR 4-Vectors:
U = dR/dτ
P = m_oU = (E_o/c²)U → [ · ] {particle}
K = (1/ћ)P = (ω_o/c²)U → [ 〜 ] {wave}
∂ = -iK

Form a chain of SR Lorentz Invariant Scalar Equations, based on those relations:
R·R = (cτ)²
U·U = (c)²
P·P = (m_oc)² = (E_o/c)²
K·K = (m_oc/ћ)² = (ω_o/c)²
∂·∂ = (-im_oc/ћ)² = -(m_oc/ћ)² = -(ω_o/c)²

The last is a fundamental quantum relation.
When applied to a Lorentz Scalar, it gives the free particle Klein-Gordon Equation (the Relativistic Quantum Wave Equation for Spin-0 Particles).
When applied to a 4-Vector, it gives the free particle Proca equation (massive case m_o > 0), and the free particle Maxwell equation (massless case m_o = 0)
For the Maxwell equation, the fact that (m_o = 0) is why you don't see the (ћ) in standard SR and EM.
The Schrödinger Equation, and hence Quantum Mechanics, is just the low-velocity (|v| << c) limiting-case of the KGE.
This is (RQM) = Relativistic Quantum Mechanics, derived from only:
--------------------------------------
5 of the Standard SR 4-Vectors.
4 really simple empirical relations between them.
1 SR rule for forming Lorentz Scalar Invariants, ie. the Minkowski Metric which gives the Lorentz Scalar Product.
--------------------------------------
As one of my physics professors (Dr. Valk - GA Tech Physics) used to say:
"Once you have the Schrödinger Equation, you have Quantum Mechanics."

I would modify this just a bit:
"Once you have the Klein-Gordon Equation, you have Relativistic Quantum Mechanics."
The Schrödinger Equation, and hence Quantum Mechanics, is just the low-velocity (|v| << c) limiting-case.
Likewise, Classical Mechanics is just the 'mixed wave' or 'non-phase aligned' limiting-case of Quantum Mechanics,
in which the divergence of a momentum state is very small compared to the magnitude-squared of the momentum state.
In other words, the limiting-case for which changing the state by a few quanta has a negligible effect on the overall state.
The Hamilton-Jacobi non-quantum limit {ћ|∇·p| << (p·p)} see Goldstein, Classical Mechanics, pg. 491

Now, since so much rides on the 4-Gradient giving the Quantum Wave eqn,
I want to emphasize that the 4-Gradient is an inherently SR object:
∂·R = ∂_μR^μ = 4: The SR Dimensionality of SpaceTime
∂[R] = ∂^μ[R^ν] = η^μν: The SR Minkowski Metric
∂_ν[R^μ'] = ∂R^μ'/∂R^ν = Λ^μ'_ν: The SR Lorentz Transform
U·∂ = γd/dt = d/dτ: The SR Proper Time Derivative
-∂[S_action] = P: An SR Particle 4-Momentum is the negative 4-Gradient of an SR Action { S_action = -P·R }
-∂[Φ_phase] = K: An SR Wave 4-WaveVector is the negative 4-Gradient of an SR Phase { Φ_phase = -K·R }
∂ = -iK: SR plane-waves fulfill -∂[Φ_phase] = K for SR functions of Phase f(Φ_phase)
∂·∂ = The SR Invariant d'Alembertian = The SR Wave Equation
No axioms of QM are required for any of these: they are all inherently SR...

The Lorentz Scalar Invariant relations among these SR 4-Vectors are essentially the same kind whether dealing with strictly SR objects or "quantum" objects.
In some sense, the "QM" connections in the diagram are "further restrictions" on things that are "already connected" in SR.
The relation between the 4-Momentum and 4-Velocity {P = m_oU} gives {E = γm_oc²}
The relation between the 4-Momentum and 4-WaveVector {P = ћK} gives {E = ћω}
Writing in the 4-Vector form shows the similarity of what most people think of as the separate objects of SR and QM.
So, this changes the paradigm of how we think GR, SR, RQM, QM, and CM all fit together...
see Correspondence Principle, Classical Limit, Newtonian Limit, Why Einstein will never be "wrong",

This is the old paradigm...

This is the new paradigm, based on the SRQM interpretation.

When one examines how EM fits in neatly on the Venn Diagram of SRQM, one sees a great similarity wrt. where the physical constants of nature arise from...
They are all Lorentz Scalar Invariants that relate one 4-Vectors to one another.
That includes the case for Divergence and Temporal Component of the EM Faraday Tensor.

And, for some more in-depth diagrams which show 4-Scalars, 4-Vectors, and 4-Tensors...

SRQM 4-Vectors, 4-Tensors, and Lorentz Scalar Diagram

SRQM + EM 4-Vector and Lorentz Scalar Diagram With Tensor Invariants

SRQM Stress-Energy and Projection Tensors Diagram

Basics

There are a couple of paradigm assumptions that we need to get clear from the start.
Relativistic stuff **IS NOT** the generalization of Classical stuff.
Classical stuff **IS** the low-velocity limiting-case approximation of Relativistic stuff { |v| << c }.
This includes Classical Mechanics and Classical QM (meaning the non-relativistic Schrödinger QM Equation).
Classical EM is for the most part already compatible with Special Relativity, although Classical EM didn't include intrinsic spin.
===
Along this same line of thought, SR Physical 4-Vectors *ARE NOT* generalizations of Classical or Quantum Physics 3-vectors.
While mathematically a Euclidean (n+1)D-vector is the generalization of a Euclidean (n)D-vector, the analogy ends there.
Minkowskian SR 4-Vectors *ARE* the primitive elements of 4D Minkowski SpaceTime.
Classical/Quantum Physics 3-vectors are just the spatial components of SR Physical 4-Vectors.
There is also a related Classical/Quantum Physics scalar which is just the temporal component of a given SR Physical 4-Vector.
The primary example is the 4-Position: (ct,x) → (ct,x,y,z)
These Classical/Quantum {scalar}+{3-vector} are the {temporal}+{spatial} "components" of an SR 4-Vector → (scalar, 3-vector).
However, different observers may see different "magnitudes" of the Classical/Quantum components from their point-of-view in SpaceTime,
while each will see the SAME actual SR 4-Vector at a given event in SpaceTime.
======
We will *NOT* be employing the commonly-(mis)used Newtonian classical limits {c→∞} and {ћ→0}.
Neither of these is a valid physical assumption, for the following reasons:
[1]
Both (c) and (ћ) are unchanging Physical Constants and Lorentz Invariants. Taking a limit where these change is nonphysical.
Many, many experiments verify that these constants have not changed over the lifetime of the universe. They are CONSTANT.
[2]
Let E = pc. If c→∞, then E→∞. Then Classical EM light rays/waves have infinite energy.
Let E = ћω. If ћ→0, then E→0. Then Classical EM light rays/waves have zero energy.

Radiometer - Proof that photons transport energy

Obviously neither of these is true in the Newtonian limit.
In Classical EM and Classical Mechanics, (c) remains a large but finite constant. Likewise (ћ) never becomes 0.
The correct way to take the limits is via:
The low-velocity non-relativistic limit {|v| << c}, which is a physically occurring situation.
The Hamilton-Jacobi non-quantum limit {ћ|∇·p| << (p·p)}, which is a physically occurring situation.
Alternately, and just to show that the Classical limit doesn't depend on the size of (ћ), this can be written as: {|∇·k| << (k·k)}
ie. when the divergence of the 3-wavevector is very small compared to the magnitude squared of the 3-wavevector
In other words, the limiting-case for which changing the state by a few quanta has a neglible effect on the overall state."
Also, I suspect that the covariant version is the actual way this should be written: {|∂·K| << (K·K)}
===
Furthermore, we will *NOT* be employing the commonly-used lazy convention of setting {c→1, ћ→1, G→1, etc.}.
While doing so "simplifies" many of the equations, one loses the power of dimensional and physical analysis.
Hey, these constants are an important aspect of nature and the physical universe. Why ignore them?
Instead, it is always possible to design equations with new variables that "hide" extra dimensional constants if so desired.
In fact, I have followed online arguments which would be solved immediately if all the units/constants had been shown from the start.
It is confusing to non-experts, and even to experts, when the correct physical units/constants are not shown.
Don't be lazy when writing equations of the universe in the beginning and ending forms.
If you want to "hide" stuff in intermediate steps, then make it clear what you are doing.
It's damn hard enough just to get all the sign conventions right in SR and GR.
Now, to those saying go "Natural Units", where the constants are set to {1}...
The main argument that I have heard is "c = 3x10⁸ m/s is a ridiculously large number to consider, so let's make the units c =1 distance unit/time unit"
Fine, set c = 1. So, v = velocity = 1 = really fast. Light travels one "light second" in one "second". Wow - that is just so descriptive... Is that a long way?
If I travel at unitless v = 1x10^-8, with no seat belt, and hit something, will I probably die? How about if I travel at v = 1x10^-7? 1x10^-6?
See where this is heading?
The whole point of a measurement system is to make things relatable to us as humans. The SI units do a pretty good job of this.
And yes, the speed of light (c) is pretty ridiculously huge on a human scale. Fact of nature. Deal with it.
We will not be using "Natural Units" here. Save them for when you just want to do pure math or complex numerical computation, not physics.
Hiding universal constants from the fundamental physical equations of nature is just really dumb otherwise...
While the choice of a system of units is arbitrary, the fact that a universal constant exists is not:
Something travelling at { |v| = c } acts fundamentally differently than something travelling at { |v| < c }, the causality difference between light-like and time-like.
And writing it that way makes way more sense than writing it as { |v| = 1 } acts fundamentally differently than something travelling at { |v| < 1 }.
Likewise, we humans operationally experience time separations differently than space separations, where the difference factor is (c). ΔX = (cΔt,Δx).
Again likewise, we operationally experience particle phenomena differently than wave phenomena, even though they are dual aspects for all known objects.
The difference factor is (ћ).
Something with a charge (q) acts differently in an EM field than something with no (q). Etc, etc.
In short, don't be lazy. Show the dimensional factors in the main equations and when teaching physics.
You can set always them to unity later to simplify things when you run your numerical simulations... which is the only time that it is truly practical to do so...
Finally, these few Invariant Relations should seal the deal:

U∙U = γ²(c²-u∙u) = c²:                            Speed of all things into the Future (4-Vectors)
(E_o/m_o) = (γE_o/γm_o) = (E/m) = c²:        Mass is concentrated Energy (SR)
|u * v_phase| = |v_group* v_phase| = c²:           Particle-Wave "Duality" Correlation (QM)
(1/ε_oμ_o) = c²:                                          The Electric (ε_o) and Magnetic (μ_o) Constants of the EM Field (EM)
-(ћ/m_o)²(∂∙∂) = c²:                                  The Klein-Gordon Relativistic Quantum Wave Eqn (spin 0), also Proca Eqn (spin 1) (RQM)
2GM/R_S = c²:                                         The GR Schwarzschild Black Hole Eqn (GR)

These also show why (c) is an unchanging Invariant - This is evidence that (c) is not variable-speed

References

Given that, let's begin:
Assume that Einstein's General Relativity (GR) and the Mathematics of GR are essentially correct and our starting point.
See also: Intro to GR, Theoretical motivation for GR, Einstein's Genius (ScienceNews), General Covariance, Principle of Covariance,
Physical theories modified by general relativity,
Note: The LIGO gravitational wave observations are making "GR-as-a-good-starting-point" more solid with each new finding...
with each confirming GR {No dispersion, Speed of gravitational wave = speed of light, and GW170814 able to include the GR-predicted polarization states} :)
Announcement on Oct 3, 2017 - Nobel Prize Physics - Gravitational Wave Detection!!
And finally, the announcement of the Binary NS merger with optical counterpart, GW170817, the first of the gravitational multi-messenger observations.
*NEWS* Dec 03,2018 - Reanalysis of prior observing run data with better algorithms finds more GW signals - now we up to 10 BBH mergers.

Consider the SR [Low Mass = {Curvature ~ 0}] limiting-case of GR.
This is equivalent to a 4D SpaceTime being a pseudo-Riemannian manifold M with a metric g^μν of signature (1,3),
and that for SR this metric g^μν is restricted (taking a limiting-case)
to being the (flat SpaceTime) Minkowski metric η^μν = Diag[+1,-1,-1,-1]{in Cartesian Form}

This gives Special Relativity (SR) ↔ Minkowski (Space /SpaceTime) ↔ Poincaré Invariance ↔ Special relativity (alternative formulations), which has the following properties:
see also Postulates of SR

The Principle of Relativity : The requirement that the equations describing the Laws of Physics have the same form in all admissible Frames of Reference
In other words, the Laws of Physics have the same form for all Inertial Observers
Mathematically this is Invariant Interval Measure ΔR·ΔR = (cΔt)² - Δr·Δr = (cΔt)² - |Δr|² = Invariant
Speed of Light (c) = Invariant Lorentz Scalar = Physical Constant
The Principle of Covariance : The requirement that physical quantities must transform covariantly,
i.e. that their measurements in different frames of reference can be unambiguously correlated (via Lorentz Transformations ) - see the Covariance Group
Lorentz Invariance (Covariance) (for rotations and boosts {A^μ' = Λ^μ'_νA^ν}: a Lorentz Transform on a 4-Vector in the group remains in the group)
Poincaré Invariance (Covariance) (for rotations, boosts, and translations {A^μ' = Λ^μ'_νA^ν + ΔA^ν}), also known as full Relativistic Invariance
The Lorentz Gamma Factor is { γ = 1/√[1 - (v/c)²] = 1/√[1 - β²] = dt/dτ}
This leads to:
Time Dilation {Δt' = γΔt}, Length Contraction {Δx' = Δx/γ}, Relativistic Mass {m = γm_o}, Relativistic Momentum {p = γm_ov}, Relativistic Kinetic Energy {E_k = E - E_o = (γ-1)m_oc²)}
Minkowski Metric η_μν = η^μν = Diag[+1,-1,-1,-1]{in Cartesian Form}, with η_ανη^νβ = η_α^β = δ_α^β and Trace [η^μν] = Tr[η^μν] = η_μνη^μν = δ_μ^μ = δ_ν^ν = 4
η_μν is the "Flat" SpaceTime Metric Tensor which is the low-mass, low-cuvature limiting-case of the GR Metric Tensor g_μν
η_μν has Metric Signature = (1,3,0), meaning counts of 1(+), 3(-), 0(null), which is also known as a Metric Signature Sum = -2 = (1) + (-3) = 1 positive + 3 negatives
which uses my preferred Metric Sign Convention (t0+ℝ) = {time: 0th-coordinate, positive(+), ℝeal}, see 4-Vectors & Lorentz Scalars Reference for reasoning behind this
4D SpaceTime M is a Lorentzian manifold subclass of a pseudo-Riemannian manifold equipped with a metric g of signature (1,3,0),
allowing tangent vectors to be classified into time-like, space-like, and light-like (null) conditions, which supplies Causal Structure. See also Tangent Space.
Visualization is aided with the use of WorldLines and Minkowski Diagrams
Elements of Minkowski SpaceTime are Events (a temporal location {t}, a spatial location {x,y,z}) combined in equivalent dimensional form,
eg. (ct,x) → (ct,x,y,z) all components have dimension [length]
These elements are represented by 4-Vectors, which are actually Tensors, which allow the coordinate-free representations of Tensor Calculus/Ricci Calculus,
sometimes denoted as 4-Tensors {the index range {0..3} = 4}, or as (1,0)-Tensors, meaning {1 upper index, 0 lower indices}.
4-Vector notation: A = ... = (a⁰,a) = (a⁰,a¹,a²,a³) → (a^t,a^x,a^y,a^z)
Tensor notation: A^μ = (a^μ) = (a⁰,aⁱ) = (a⁰,a¹,a²,a³) → (a^t,a^x,a^y,a^z)
4-Vectors can be used to represent Physical Properties, and relations (equations) between 4-Vectors represent Physical Laws = Laws of Science
ex. 4-Momentum P = (E/c,p) represents the physical properties of (temporal) Energy E and (spatial) 3-momentum p
{ P = m_oU = (E_o/c²)U} and { P·P = (E/c,p)·(E/c,p) = (E/c)² - p·p = (E_o/c)² = (m_oc)²} are physical laws.
see Invariant Mass, Mass in Special Relativity, Mass-Energy Equivalence
Scalar Products ( Inner products ) of 4-Vectors give Invariant Lorentz Scalars {(0,0)-Tensors} ex. A·B = A^μη_μνB^ν = A'·B' = Scalar Invariant S
Tensor Products ( Outer Products ) of 4-Vectors give higher index tensors {(2,0)-Tensors, (3,0)-Tensors, etc.} ex. F^μν = (∂^μA_EM^ν - ∂^νA_EM^μ)
Index raising and lowering, along with the previous operations, can be used to create tensors of mixed rank {(m,n)-Tensors} ex. η_ανη^νβ = δ_α^β
The Isometry Group (the set of all "distance-preserving" maps) of Minkowski SpaceTime is the Poincaré Group
Poincaré Group Symmetry : P = SO⁺(1,3) ⋉ ℝ^1,3(a non-Abelian Lie Group with 10 Generators )
Poincaré Generators = { 3 rotations Jⁱ + 3 boosts Kⁱ + 1 time-translation P⁰ + 3 space-translations Pⁱ, with i = 1..3}
Poincaré (10 "SpaceTime Generators") = Lorentz (6 "SpaceTime Rotation/Boosts" anti-symmetric M^μν) + Translations (4 "SpaceTime Translations" P^μ)
where the Lorentz Group Rotations mix orthogonal space directions; Lorentz Group Boosts mix time with a space direction
However, the double cover P̃ = SL(2,ℂ) ⋉ ℝ^1,3 = Spin(1,3) ⋉ ℝ^1,3 is the total Symmetry Group of Minkowski SpaceTime :
i.e. the connected double cover of the Poincaré Group, as this includes particle symmetries and the ability to describe spin 1/2 fields.
SL(2,ℂ) is the group of complex (2x2) matrices with unit determinant.

New X'^μ

4-Tensor Antisymmetric
Lorentz Transform M^μν
Rotations j = M^ab
Boosts k = M^0b = -M^b0
3 + 3 = 6

Original X^μ

4-Vector
SpaceTime Translation ΔX^μ ~ e^P^μ
Time Translation H = P⁰
Space Translation p = Pⁱ
1 + 3 = 4

X'⁰

X'¹

X'²

X'³

= e^

	M⁰¹	M⁰²	M⁰³
M¹⁰		M¹²	M¹³
M²⁰	M²¹		M²³
M³⁰	M³¹	M³²

X⁰

X¹

X²

X³

+e^

P⁰

P¹

P²

P³

Total of 6 + 4 = 10 parameters
Poincaré Transform = Lorentz Transform + SpaceTime Translation
X^μ' = Λ^μ'_ν X^ν + ΔX^μ'
with Λ^μ'ν = exp[1/2 ωαβM^αβ]^μ’ν
ΔX^μ' = exp[X∙P]^μ’
where colors indicate

temporal

spatial

mixed

The (10) one-parameter groups can be expressed directly as exponentials of the generators:
U[I, (0,λâ)] = e^(-iλâ·p): (3) Linear Momentum p
U[I, (a⁰,0)] = e^(ia⁰·H) = e^(ia⁰·P⁰): (1) Hamiltonian = Energy = Temporal Momentum H
U[Λ(iλθ̂/2), 0] = e^(iλθ̂·j): (3) Angular Momentum j
U[Λ(λφ̂/2), 0] = e^(iλφ̂·k): (3) Rotationless Boost k
The Poincaré Algebra is the Lie Algebra of the Poincaré Group :
============
Covariant form: P = Generator of Translations, M = Generator of Lorentz Transformations (Rotations & Boosts)
These are the commutators of the the Poincaré Algebra :
[X^μ, X^ν] = 0^μν
[P^μ, P^ν] = -iћq(F^μν) if interacting with EM field; otherwise = 0^μν for free particles
M^μν = (X^μP^ν - X^νP^μ) = iћ(X^μ∂^ν - X^ν∂^μ)
[M^μν, P^ρ] = iћ( η^ρνP^μ - η^ρμP^ν)
[M^μν, M^ρσ] = iћ(η^νρM^μσ + η^μσM^νρ + η^σνM^ρμ + η^ρμM^σν)

Translational Operator	∂^μ	K^μ	P^μ
Equivalent	= ∂^μ	= i∂^μ	= iћ∂^μ
Normal Commutator	[∂^μ, X^ν] = η^μν	[K^μ,X^ν] = iη^μν	[P^μ, X^ν] = iћη^μν
Reversed Commutator	[X^ν, ∂^μ] = -η^μν	[X^ν, K^μ] = -iη^μν	[X^ν, P^μ] = -iћη^μν

Rotational Momentum Operator M	M^μν	M^μν	M^μν	Dimensionless Rotational Operator O	O^μν	O^μν	O^μν
Equivalent	= iћ(X^μ∂^ν - X^ν∂^μ)	= ћ(X^μK^ν - X^νK^μ)	def. = (X^μP^ν - X^νP^μ)	Equivalent	def. = (X^μ∂^ν - X^ν∂^μ)	= (1/i)(X^μK^ν - X^νK^μ)	= (1/iћ)(X^μP^ν - X^νP^μ)
Normal Commutator	[M^μν, ∂^ρ] = iћ(η^ρν∂^μ - η^ρμ∂^ν)	[M^μν, K^ρ] = iћ(η^ρνK^μ - η^ρμK^ν)	[M^μν, P^ρ] = iћ(η^ρνP^μ - η^ρμP^ν)	Normal Commutator	[O^μν, ∂^ρ] = (η^ρν∂^μ - η^ρμ∂^ν)	[O^μν, K^ρ] = (1/i)(η^ρνK^μ - η^ρμK^ν)	[O^μν, P^ρ] = (1/iћ)(η^ρνP^μ - η^ρμP^ν)
Reversed Commutator	[∂^ρ, M^μν] = -iћ(η^ρν∂^μ - η^ρμ∂^ν) = iћ(η^ρμ∂^ν - η^ρν∂^μ)	[K^ρ, M^μν] = -iћ(η^ρνK^μ - η^ρμK^ν) = iћ(η^ρμK^ν - η^ρνK^μ)	[P^ρ, M^μν] = -iћ(η^ρνP^μ - η^ρμP^ν) = iћ(η^ρμP^ν - η^ρνP^μ)	Reversed Commutator	[∂^ρ, O^μν] = -(η^ρν∂^μ - η^ρμ∂^ν) = (η^ρμ∂^ν - η^ρν∂^μ)	[K^ρ, O^μν] = -(1/i)(η^ρνK^μ - η^ρμK^ν) = (1/i)(η^ρμK^ν - η^ρνK^μ)	[P^ρ, O^μν] = -(1/iћ)(η^ρνP^μ - η^ρμP^ν) = (1/iћ)(η^ρμP^ν - η^ρνP^μ)

============
Component form: Rotations J_i = -ε_imnM^mn/2, Boosts K_i = M_i0
[J_m,P_n] = iε_mnkP^k
[J_m,P₀] = 0
[K_j,P_k] = iη_jkP₀
[K_j,P₀] = -iP_j
[J_m,J_n] = iε_mnkJ^k
[J_m,K_n] = iε_mnkK^k
[K_m,K_n] = -iε_mnkJ^k, a Wigner Rotation resulting from consecutive boosts
[J_m + iK_m,J_n - iK_n] = 0
============
Poincaré Algebra has 2 Casimir Invariants = Operators that commute with all of the Poincaré Generators
These are {P² = P^μP_μ = (m_oc)², W² = W^μW_μ = -(m_oc)²j(j + 1) }, with W^μ = (-1/2)ε^μνρσJ_νρP_σ as the Pauli-Lubanski Pseudovector
Alt Def: W^μ = (1/2)ε^μνσρP_νM_σρ = (1/2)ε^μνσρM_σρP_ν
[P²,P⁰] = [P²,Pⁱ] = [P²,Jⁱ] = [P²,Kⁱ] = 0: Hence the 4-Momentum Magnitude squared commutes with all Poincaré Generators
[W²,P⁰] = [W²,Pⁱ] = [W²,Jⁱ] = [W²,Kⁱ] = 0: Hence the 4-SpinMomentum Magnitude squared commutes with all Poincaré Generators
Furthermore:
[P_μ,P_ν] = 0
[W_μ,P_ν] = 0
(1/i)[W^μ,M_σρ] = δ^μ_σW_ρ - δ^μ_ρW_σ
(1/i)[W^μ,W^ν] = ε^μνσρP_σW_ρ
****
Very importantly, the Poincaré group has Casimir Invariant Eigenvalues = { Mass m, Spin j },
hence Mass *and* Spin are purely SR phenomena, no QM axioms required!
See also: Relativistic Center of Mass, with good section on SR Casimir Invariants { Mass & Spin } ****

This Representation of the Poincaré Group or Representation of the Lorentz Group
is known as Wigner's Classification in Representation Theory of Particle Physics
Apparently still true in GR is Infinitesimal Invariant Interval Measure dR·dR = (cdτ)² = (cdt)² - dr·dr = (cdt)² - |dr|²

Justification of the SRQM treatise

Universal physical constants that are Lorentz Scalars (with experimental verification of the Non-time-variation of fundamental constants, Baez website constants, Baez website variability,):
Speed of Light (c), Measurement of (c)
Planck Constant (h) and reduced Planck Constant (ћ): with { ћ = h/2π }, Measurement of (h)
EM Elementary Charge (e), Measurement of (e)
Electric constant = Vacuum Permittivity (ε_o), Magnetic constant = Vacuum Permeability (μ_o): Really just one independent constant due to { ε_oμ_o = 1/c² }
Gravitational Constant (G)
Electron Rest Mass (m_e)
Boltzmann Constant (k = k_B)

(c) = Sqrt[U∙U]
(ћ) = [P∙U]/[K∙U]
U·F^αν = (1/q)F
∂·F^αν = (μ_o)J = (1/c²ε_o)J
(m_o) = [P∙U]/[U∙U]
G_μν + Λg_μν = (8πG/c4)T_μν with G_μν = R_μν - (R/2)g_μν

Distant Quasars Show That Fundamental Constants Never Change (Jan 2017),
Synopsis: Pinpointing Planck’s Constant with GPS (Mar 2012),
Viewpoint: Time Trials for Fundamental Constants (Nov 2014),

See also: Coupling Constant,
Fine Structure Constant { α = (1/4πε_o)(e²/ћc) = (μ_o/4π)(ce²/ћ) },
Gravitational Coupling Constatnt { α_G = Gm_e²/ћc },
Note that these are made up from the Lorentz Scalar constants from above...

Mathematician Emmy Noether changed the face of physics, linking two important concepts in physics: conservation laws and symmetries

Now, just to give some more background on where this is all heading:

Special Relativity (SR) and Quantum Mechanics (QM) are completely compatible in Relativistic Quantum Mechanics (RQM)
The combination of both theories leads to Relativistic Wave Equations (RWE),
The relativistic formulation is more successful than the original "classical" quantum mechanics:
The prediction of antimatter, electron spin, spin magnetic moments of elementary spin-1/2 fermions, fine structure, and quantum dynamics of charged particles in electromagnetic fields.
The most basic of the RQM equations (spin 0, massive) is the Klein-Gordon Equation
The next level RQM equation (spin 1/2, massive) is the Dirac Equation
And the next RQM equation (spin 1, massless) is the Maxwell Equation, which is actually standard EM
The formalism developed then leads smoothly into Quantum Field Theory (QFT) and Gauge Theory via Second Quantization (multiple particles = field quantization).
Examples of these are: Quantum Electrodynamics (QED) and Yang-Mills Theory and The Standard Model

RQM is required for various theorems:
Spin-Statistics Theorem, CPT Theorem, Coleman-Mandula Theorem, Haag's Theorem, Weinberg-Witten Theorem, etc.
Various QM phenomena are derivable once you have RQM:
Quantum Superposition, Pauli Exclusion Principle, Canonical Commutation Relation, Heisenberg Uncertainty, etc.
Newtonian Limit of the (spin 0) RQM Klein-Gordon Equation is the QM Schrödinger Equation (First Quantization)
Newtonian Limit of the (spin 1/2) RQM Dirac Equation is the QM Pauli Equation

These are the free particle versions of the listed equations (no interaction with a potential)
All based on the fundamental equation we derived in the Roadmap above.
∂·∂ = (-im_oc/ћ)² = -(m_oc/ћ)² = -(ω_o/c)²

Standard Model Elementary Particle				Relativistic Wave Equations (RWE)	Relativistic Wave Equations (RWE)	Newtonian Limit ( \|v\| << c )
Particle Type	Spin	Statistics	Field	RQM Massless (m_o = 0)	RQM Massive (m_o > 0)	QM Massive (m_o > 0)
Fundamental	0	Boson	Lorentz Scalar ψ	Scalar Wave (∂·∂)ψ = 0	Klein-Gordon Equation (∂·∂ + (m_oc/ћ)²)ψ = 0	Schrödinger Equation (iħ∂_t)ψ ~ [(m_oc²) - (ħ∇)²/2m_o]ψ
Fundamental	1/2	Fermion	Spinor Ψ	Weyl Equation [(iγ^μ∂_μ)]Ψ = 0 → [(σ^μ∂_μ)]Ψ = 0	Dirac Equation, Majorana Equation [(iγ^μ∂_μ) - (m_oc/ћ)]Ψ = 0 (Γ^μP_μ)Ψ = (m_oc)Ψ iћ(Γ^μ∂_μ)Ψ = (m_oc)Ψ	Pauli Equation (iħ∂_t)Ψ ~ [(m_oc²) + (σ·p)²/2m_o]Ψ
Fundamental	1	Boson	4-Vector A	Maxwell Equation (∂·∂)A = 0	Proca Equation (∂·∂ + (m_oc/ћ)²)A = 0	?

Composites	3/2	Fermion	Spinor-Vector	Majorana Rarita-Schwinger	Rarita-Schwinger Equation
??	2	Boson	(2,0)-Tensor	Graviton??

Each of these can be free particle, particle with source, or particle with QM source:
eg.
(∂·∂)A^ν = 0^ν: The Free Classical Maxwell EM Equation {no source, no spin effects}
(∂·∂)A^ν = μ_oJ^ν: The Classical Maxwell EM Equation {with 4-Current J source, no spin effects}
(∂·∂)A^ν = q(ψ̅ γ^ν ψ): The QED Maxwell EM Spin-1 Equation {with QED source, including spin effects}

These are the minimal-coupled versions of the listed equations (interaction with an EM potential)

Standard Model Elementary Particle				Relativistic Wave Equations (RWE)	Relativistic Wave Equations (RWE)	Newtonian Limit ( \|v\| << c )
Particle Type	Spin	Statistics	Field	RQM Massless (m_o = 0)	RQM Massive (m_o > 0)	QM Massive (m_o > 0)
Fundamental	0	Boson	Lorentz Scalar ψ	Scalar Wave (D·D)ψ = 0	Klein-Gordon Equation (D·D + (m_oc/ћ)²)ψ = 0	Schrödinger Equation (iħ∂_tT)ψ ~ [qφ + (m_oc²) + (-iħ∇_T -qa)²/2m_o]ψ (iħ∂_tT)ψ ~ [V + (-iħ∇_T -qa)²/2m_o]ψ : with [V = qφ + (m_oc²)]
Fundamental	1/2	Fermion	Spinor Ψ	Weyl Equation ?	Dirac Equation, Majorana Equation Γ^μ(P_μ-qA_μ)Ψ = (m_oc)Ψ Γ^μ(iћ∂_μ-qA_μ)Ψ = (m_oc)Ψ	Pauli Equation (iħ∂_tT)Ψ ~ [qφ + (m_oc²) + [σ·(p_T -qa)]²/(2m_o)]Ψ (iħ∂_tT)Ψ ~ [qφ + (m_oc²) + ([(p_T -qa)]² - ћq[σ·B])/(2m_o)]Ψ
Fundamental	1	Boson	4-Vector A	Maxwell Equation (∂·∂)A = 0 (∂·∂)A^ν = μ_oJ^ν: Classical source (∂·∂)A^ν = q(ψ̅ γ^ν ψ): QED source	Proca Equation	?

Composites	3/2	Fermion	Spinor-Vector	Majorana Rarita-Schwinger	Rarita-Schwinger Equation
??	2	Boson	(2,0)-Tensor	Graviton??

This website dedicated to "THE" Master Physics Guru: Albert Einstein
Creator/Discoverer/Explorer of SR and GR, and somewhat grudgingly, QM
The Albert Einstein Memorial below is at GA Tech, the Georgia Institute of Technology, my Alma Mater.

Written" on the papers Einstein is holding:
===================================
R_μν - (1/2)g_μνR = κT_μν (the theory of GR)
eV = hν - A (the PhotoElectric Effect)
E = mc² (the Equivalence of Energy and Matter)
===================================

Correlates to:
==========
GR
QM
SR
==========

Einstein's genius changed science's perception of gravity: General relativity has grown more important than it was in Einstein's day (Oct 2015),
Einstein and Quantum Mechanics: It’s Not What You Think- A.D.S.
===
Einstein is well known for his rejection of quantum mechanics in the form it emerged from the work of Heisenberg, Born and Schrodinger in 1926. Much less appreciated are the many seminal contributions he made to quantum theory prior to his final scientific verdict, that the theory was at best incomplete. Einstein fathered many conceptual breakthroughs and they need to be placed in historical context. Stone argues that Einstein, much more than Planck, introduced the concept of quantization of energy in atomic mechanics. Einstein proposed the photon, the first force-carrying particle discovered for a fundamental interaction, and put forward the notion of wave-particle duality, based on sound statistical arguments 14 years before De Broglie’s work. He was the first to recognize the intrinsic randomness in atomic processes, and introduced the notion of transition probabilities, embodied in the A and B coefficients for atomic emission and absorption. He also preceded Born in suggesting the interpretation of wave fields as probability densities for particles, photons, in the case of the electromagnetic field. Finally, stimulated by Bose, he introduced the notion of indistinguishable particles in the quantum sense and derived the condensed phase of bosons, which is one of the fundamental states of matter at low temperatures. His work on quantum statistics in turn directly stimulated Schrodinger towards his discovery of the wave equation of quantum mechanics. It was only due to his rejection of the final theory that he is not generally recognized as the most central figure in this historic achievement of human civilization - quantum mechanics.
===
An Einstein We Didn't Know: Despite his famed line about God ‘not playing dice,’ evidence in letters shows that Einstein was the living spirit behind quantum mechanics (May 2018),

Now, some basics about SR 4-Vectors...
4-Vector V^μ = (V⁰,Vⁱ) = (V⁰,V¹,V²,V³)

V⁰	V¹	V²	V³
temporal part = V⁰	spatial part = Vⁱ

SR Light Cone

SR 4-Vectors - Notation, Conventions, Properties

*Note* Numeric subscripts and superscripts on variables inside the vector parentheses typically represent tensor indices, not exponents.

In the following, I use the Time-0th-Positive-ℝeal (t0+ℝ) SR metric sign convention, also known as the West Coast convention or the Particle Physics convention.
η_μν = η^μν = diagonalMatrix[+1,-1,-1,-1] in Cartesian coords.
I use this convention primarily because the note it starts with is a "Positive One" :)
Actually, it reduces the number of minus signs in Lorentz Scalar Magnitudes, since there seem to be many more time-like physical 4-Vectors than space-like.
More importantly, this sign convention is the one matched by the QM Schrödinger Relations later on...
And even more importantly, it's the convention that matches the sensible definition of Vector Projection along a Worldline.
Also, imaginary numbers (i) ONLY come into play when QM is discovered. See also MisnerThorneWheeler "(ict) put to the sword".

Alternate conventions are variations of (t: 0 or 4, + or -, ℝ or ℂ), meaning:
Time: is either the 0th or 4th component, {time(+),space(-)} or {time(-),space(+)} in the metric, and time component is ℝ~(ct) or ℂ~(ict).
Some common alternate ones are (t0-ℝ), (t4+ℝ), and (t4-ℝ), and some older ones use ℂ in either the 4-vector or metric temporal component.
Also, many authors hide the speed-of-light (c) by setting it to (c →1), which I find very annoying.
Wrong way: 4-Position X = (t,x,y,z) has physical dimensions of [time], no, wait, [length], no, ughhh...
Right way: 4-Position X = (ct,x,y,z) has physical dimesions of [length], Yes. No ambiguity.
Wrong way: {E = m}: hmmmm... Energy is identical to mass... Heat = Gravitational Potential = Chemical Bonds... Well, not exactly... and all Energy has dimensional units of [mass]... Well, not exactly...
Right way: {E = mc²}: Mass is a form of incredibly concentrated Energy. Yes. Energy has dimensional units of [mass]*[length]²/[time]². Yes. Energy can take on different forms.
See the difference. Basic Physics Rule: Show the units and the symbolic universal constants!.
Anyway, any of these notations can be used as long as one adheres to the same choice in a given derivation/calculation/equation/essay/lecture.

**Always check which convention is being used when reading other SR and GR texts. It will affect where the minus-signs go.**

I always choose to have the 4-Vector (or 3-vector) refer to the ^{upper index} tensor of the same name.
4-Vector A = A^μ = (a⁰,a¹,a²,a³) = (a⁰,a) = (a⁰,aⁱ)
3-vector a = aⁱ = (a¹,a²,a³)
In addition, I like the convention of having the (c) factor in the temporal part for correct dimensional units. {eg. 4-Position R = (ct,r) overall units = [length]}
This also allows the SR 4-Vector name to match the classical 3-vector name, which is useful when considering Newtonian limiting-cases.

I use:
UPPER CASE BOLD, Greek index range = {0..3}, for 4-Vectors (A = A^μ), and sometimes an under-line symbol ( A ) when writing-by-hand.
lower case bold, Latin index range = {1..3}, for 3-vectors (a = aⁱ), and sometimes an over-arrow (vector) symbol ( a⃑ ) when writing-by-hand.

Note that the ( ⁱ ) in the index is not the imaginary ( i ). Try to use other (non-i) index letters when imaginary (i) is elsewhere in a tensor equation to avoid confusion.
Likewise, try to use different index letters than the other variables in an equation.
Many, many other texts do not use different letters. It can be very confusing and ambiguous.

I also adopt Wolfgang Rindler's convention of using:
lower case bold (e) for the Electric field 3-vector e = eⁱ → (e^x,e^y,e^z)
lower case bold (b) for the Magnetic field 3-vector b = bⁱ → (b^x,b^y,b^z)
*Note* (e) and (b) are not 4-Vectors, nor the spatial parts of 4-Vectors, but combined are components of the 2-index Faraday EM Tensor F^μν
You can get close though...
4-EM Force F_EM = γq[ (u·e)/c, (e) + (u⨯b) ]
In a rest frame: F_EMo = q(0,e), so (e) is the spatial part of (F_EMo/q), but only in the rest frame.
e = eⁱ = cFⁱ⁰ and b = b^k = -(1/2)ε_ij^kF^ij

Following the same idea, I am also implementing:
lower case bold (a) for the Electromagnetic 3-vector VectorPotential (spatial component)
while retaining the historical (φ) for the Electromagnetic ScalarPotential (temporal component)
A = (φ/c,a) → (φ/c,a^x,a^y,a^z)

Also, I use the "at-rest" notation "naught" (_o) to differentiate from the 0-index component of 4-Vector.
Thus
v⁰ is the 0th-index component of V^μ = (v⁰,v¹,v²,v³)
v₀ is the 0th-index component of V_μ = (v₀,v₁,v₂,v₃)
v_o is the "at-rest" Lorentz Scalar, which usually relates two separate 4-Vectors, eg. V^μ = v_oT^μ
v⁰_o is the "at-rest" 0th-index component and Lorentz scalar for V·T = v⁰_o
Based on this, I prefer restmass = m_o instead of m₀.

All SR 4-Vectors have the following properties:
==============================================

A = A^μ = (a⁰,aⁱ) = (a⁰,a) = (a⁰,a¹,a²,a³) → (a^t,a^x,a^y,a^z): A typical 4-Vector (contravariant = ^{upper index})

A_μ = (a₀,a_i) = (a₀,-a) = (a₀,a₁,a₂,a₃) → (a_t,a_x,a_y,a_z): A typical 4-Covector (covariant = _{lower index})
= (a⁰,-a) = (a⁰,-a¹,-a²,-a³) → (a^t,-a^x,-a^y,-a^z):

with A_μ = η_μνA^ν and A^μ = η^μνA_ν: Tensor index lowering and raising with the Minkowski Metric η^μν

One can also use A = A^μ = (A⁰, Aⁱ) = (A⁰,A¹,A²,A³) to demonstrate 4-Vector mathematics,
but once you start doing physics, most of the component values (physical variable names) are lowercase letters,
An exception is that the Energies are usually uppercase E = Energy, U = PotentialEnergy, H = Hamiltonian.
The energy-densities are usually lowercase: u_e = ε = e = ρ_e = EnergyDensity, u = PotentialEnergyDensity, etc.
Therefore, I prefer A = A^μ = (a⁰,aⁱ) = (a⁰,a) = (a⁰,a¹,a²,a³), which also avoids the weirdness of (A⁰,a).
However, there are a few cases where the Uppercase letters are helpful.
4-Velocity U = U^μ = (U⁰,Uⁱ) = γ(c,u) = (γc,γu)
The relativistic spatial component of 4-Velocity is ( Uⁱ = γuⁱ = γu ), which is actually equal to the Lorentz gamma factor (γ) * spatial Newtonia 3-velocity ( u = uⁱ ).
This type of thing also occurs in the 4-Acceleration and the 4-Force, and a few others.

The main idea that makes a generic 4-Vector into an SR 4-Vector is that it must transform properly according to a Lorentz Transformation Λ^μ'_ν (or sometimes written as L^μ'_ν).
(A^μ' = Λ^μ'_νA^ν) with Λ^μ'_ν as the Lorentz Transformation tensor. { β = v/c = β_xx̂ + β_yŷ + β_zẑ} and {γ = 1/√[1-β²]}
with both (A^μ' and A^ν) both representing the same kind of SR 4-Vector (primed index after transform, unprimed index before transform).
We also have (Tr[Λ^μ_ρ Λ^ν_σ] = Λ^μ_ρ η_μν Λ^ν_σ = η_ρσ) as a general rule.
Likewise: { (Λ^-1)^ν_μ = Λ_μ^ν } and [(Λ^-1)^T]^μ_ν = Λ^ν_μ }

Typical Lorentz Transformation, for a frame shift in the x̂ -direction:
Λ^μ'_ν = {for x̂-boost}

γ	-β_xγ	0	0
-β_xγ	γ	0	0
0	0	1	0
0	0	0	1

So A^μ' = (a^t, a^x, a^y, a^z)' = Λ^μ'_νA^ν = (γa^t - γβ_xa^x,-γβ_xa^t + γa^x, a^y, a^z){for x̂ -boost Lorentz Transform}

This can also be written as a hyperbolic rotation:

cosh[ζ]	-sinh[ζ]	0	0
-sinh[ζ]	cosh[ζ]	0	0
0	0	1	0
0	0	0	1

where {ζ = acosh[γ]} is a "rapidity"
γ = cosh[ζ], β = tanh[ζ], γβ = sinh[ζ],

Note that this is very similar to a standard spatial rotation:
R^μ'_ν = {for z-rotation}

1	0	0	0
0	cos[θ]	-sin[θ]	0
0	sin[θ]	cos[θ]	0
0	0	0	1

So A^μ' = (a^t, a^x, a^y, a^z)' = Λ^μ'_νA^ν = (γa^t - γβ_xa^x,-γβ_xa^t + γa^x, a^y, a^z){for x̂ -boost Lorentz Transform}
An Inverse Lorentz Transformation is equivalent to just reversing the direction of the boost, i.e. change the signs on the β's.
So (a^t, a^x, a^y, a^z)' = (γa^t + γβ_xa^x, γβ_xa^t + γa^x, a^y, a^z){for x̂ -boost Inverse Lorentz Transform}

Being a little more thorough, we can do a Lorentz Transform in the ( β = βn̂ ) direction:
Using:
(a⁰)' = γ(a⁰ - β·a) The temporal direction gets transformed
(a_∥)' = γ(- βa⁰ + a_∥) Only the parallel spatial direction gets transformed
(a_⟂)' = (a_⟂) The perpendicular spatial direction remains unchanged

A^μ' =
= (a⁰,a_∥ + a_⟂)'
= (a⁰,a)'
= Λ^μ'_νA^ν
= (γa⁰ - γβ·a, - γβa⁰ + γa_∥ + a_⟂)
= (γa⁰ - γβ·a, - γβa⁰ + γa_∥ + a - a_∥)
= (γa⁰ - γβ·a, - γβa⁰ + (γ-1)a_∥ + a)
= (γa⁰ - γβ·a, - γβa⁰ + (γ-1)(β·a)β/|β|² + a)

So,
Temporal component: (a⁰)' = γ(a⁰ - β·a)
Spatial component: (a)' = (- γβa⁰ + (γ-1)(β·a)β/|β|² + a)

General Lorentz Transformation, for a frame shift in any direction n̂:
Λ^μ'_ν = {for n̂-boost}

γ	-β_xγ	-β_yγ	-β_zγ
-β_xγ	1 + (γ-1)(β_x/β)²	( γ-1)(β_xβ_y)/(β)²	( γ-1)(β_xβ_z)/(β)²
-β_yγ	( γ-1)(β_yβ_x)/(β)²	1 + ( γ-1)(β_y/β)²	( γ-1)(β_yβ_z)/(β)²
-β_zγ	( γ-1)(β_zβ_x)/(β)²	( γ-1)(β_zβ_y)/(β)²	1 + ( γ-1)(β_z/β)²

An SR 4-Vector will still represent the same physical object after a Lorentz Transformation is applied,
in exactly the same way that it represents the same object after a Translation or Rotation Transformation is applied.

The Einstein Summation Rule: A duplicated ^upper/_lower index pair is always summed. Greek index (0..3), Latin index (1..3)
A^μB_μ = Σ_{( μ = 0..3 )}[a^μb_μ] = + a⁰b₀ + a¹b₁ + a²b₂ + a³b₃
AⁱB_i = Σ_{( i = 1..3 )}[aⁱb_i] = + a¹b₁ + a²b₂ + a³b₃

One can form a Lorentz Scalar Product Invariant by taking the SR Inner Product (4D dot product) of 4-Vectors or the SR Trace of a (2,0)-Tensor.
{let C^μν = A^μ⊗B^ν = A^μB^ν in the following, just remember that in general not all C^μν can necessarily be written as a product of A^μ and B^ν}
The SR Trace is technically C = C^μ_μ = C_ν^ν = η_μνC^μν = The sum of diagonal components on the mixed-index tensor.
The SR Trace operator Tr[] = η_μν[ ^μν] = Diag(+1,-1,-1,-1)[ ^μν] = ( ^μ)·( ^ν)
Tr[C^μν] = C^μ_μ = C_ν^ν = η_μνC^μν = η_μνA^μB^ν = A^μη_μνB^ν = A^μB_μ = A_νB^ν = A·B = Lorentz Scalar Invariant

All of the following are equivalent:
A·B = A^μη_μνB^ν = Tr[A^μB^ν] = Tr[C^μν] = C^μ_μ = C_ν^ν = η_μνC^μν = + c⁰⁰ - c¹¹ - c²² - c³³ + (all other elements zero) = Just the diagonal
A·B = A^μη_μνB^ν = + a⁰b⁰ - a·b = + a⁰b⁰ - a¹b¹ - a²b² - a³b³ + (all other products zero)
A·B = A^μη_μνB^ν = A_νB^ν = + a₀b⁰ + a₁b¹ + a₂b² + a₃b³
A·B = A^μη_μνB^ν = A^μB_μ = + a⁰b₀ + a¹b₁ + a²b₂ + a³b₃
A·B = (+a⁰b⁰ - a·b) = Lorentz Scalar Invariant : probably the most commonly used form for SR physics.
{ex. K·X = (ωt - k·x) = -Φ}
{ex. P·P = (E²/c² - p·p) = (m_oc)²}

Proof that this is an invariant:
A'·B' = A^μ'η_μ'ν'B^ν' = (Λ^μ'_αA^α) η_μ'ν'(Λ^ν'_βB^β) = (Λ^μ'_αη_μ'ν'Λ^ν'_β) A^αB^β = (Λ_ν'αΛ^ν'_β) A^αB^β = (η_αρΛ^ρ_ν'Λ^ν'_β) A^αB^β = (η_αρδ^ρ_β) A^αB^β = (η_αβ) A^αB^β = A^α(η_αβ)B^β = A·B

If the scalar product is between tensors with multiple indices, then one should use tensor indices for clarity, otherwise the equation remains ambiguous.
{eg. U·F^μν = U^α·F^μν = ? → U^αη_αμF^μν = U_μF^μν or U^αη_ανF^μν = U_νF^μν}
Although, I will occasionally use the ambiguous form simply to emphasize a similarity to other 4-Vector equations.

Importantly, A·B = (a⁰_ob⁰) = A_o·B and A·A = (a⁰_o)² = A_o·A_o, the Lorentz Scalar Product can quite often be set to the "rest values" of the temporal component.
This occurs when the 4-Vector A is Lorentz-Boosted (A^μ' = Λ^μ'_νA^ν) to a frame in which the spatial component is zero: A = (a⁰,a) → A_o = (a⁰_o,0)

In this metric convention:
[A·B > 0] → Time-Like
[A·B = 0] → Light-Like/Photonic/Null
[A·B < 0] → Space-Like

4-Vectors are actually tensors, which themselves may be a function of a 4-Vector:
4-Scalar = (0,0)-Tensor: Φ[X^μ] 4-Scalar function of 4-Position
4-Vector = (1,0)-Tensor: A^α[X^μ] 4-Vector function of 4-Position
4-Tensor = (2,0)-Tensor: g_αβ[X^μ] 4-Tensor function of 4-Position
In other words, the tensors may have different values depending on the 4-Position

The Invariant Rest Value of the Temporal Component Rule:
==========================================================
β = v/c = u/c
4-UnitTemporal T = γ(1,β) = U/c
4-Velocity U = γ(c,u) = cT
Generic 4-Vector A = (a⁰,a)
A·T = (a⁰,a)·γ(1,β) = γ(a⁰*1 - a·β) = γ(a⁰ - a·β) = (1)(a⁰_o - a·0) = a⁰_o
A·T = a⁰_o
The Lorentz Scalar product of any 4-Vector with the 4-UnitTemporal T gives the Invariant Rest Value of the Temporal Component.
This makes sense from a vector viewpoint - you are taking the projection of the generic vector along a unit-length vector in the time direction.
Also, I use the "at-rest" notation "naught" (_o) to differentiate from the 0-index component of 4-Vector.
Thus
a⁰ is the 0th-index component of A^μ = (a⁰,a¹,a²,a³)
a₀ is the 0th-index component of A_μ = (a₀,a₁,a₂,a₃)
a_o is the "at-rest" Lorentz Scalar, which usually relates two separate 4-Vectors, eg. A^μ = a_oT^μ
a⁰_o is the "at-rest" 0th-index component and Lorentz scalar for A·T = a⁰_o
Based on this, I prefer restmass = m_o instead of m₀.

A·U = c*a⁰_o
The Lorentz Scalar product of any 4-Vector with the 4-Velocity gives c*Invariant Rest Value of the Temporal Component.
It's the same thing, just multiplied by (c).
I will call these (A·T = a⁰_o or A·U = c*a⁰_o) the "Invariant Rest Value of the Temporal Component Rule".
This will get used extensively later on...
There is an analogous relation with the "aligned" 4-UnitSpatial S. ("aligned" because there are 3 spatial dimensions possible)

Here is something interesting:
We know that (γβ²)(P_T·U) = p_T·u
(γ² - 1) = γ²β²
(γ - 1/γ) = γβ²
A·U = (a⁰,a)·γ(c,u) = γ(a⁰*c - a·u) = γ(ca⁰ - a·u) = (1)(ca⁰_o - a·0) = ca⁰_o
(γβ²)(A·U) = (γ - 1/γ)(A·U) = γ(A·U) - (1/γ)(A·U) = γ(ca⁰_o) - (1/γ)(γ(a⁰*c - a·u)) = (ca⁰) - (a⁰*c - a·u) = (a·u)
If A is ~ to U, then (γβ²)(A·U) = (a·u)

The Scalar Product-Gradient-Position Relation:
=============================================
4-Position X = (ct,x)
4-Gradient ∂ = ∂_X = (∂_t/c,-∇)
Generic 4-Vector A = (a⁰,a) ≠ A[X], which is not a function of X

A·X = (a⁰,a)·(ct,x) = (a⁰*ct - a·x) = Θ is equivalent to ∂[Θ] = ∂[A·X] = A

{ A·X = Θ } ↔ { ∂[Θ] = A}

Proof:
Let A·X = Θ
∂[Θ] = ∂[A·X] = ∂[A]·X + A·∂[X] = (0) + A^κ·∂^μ[X^ν] = A^κ·η^μν = A^κη_κμη^μν = A_μη^μν = A^ν = A

Let ∂[Θ] = A
A·X = (a⁰,a)·(ct,x) = (a⁰*ct - a·x) = (∂_t[Θ]/c*ct + ∇[Θ]·x) = (∂_t[Θ]*t + ∇[Θ]·x) = Θ

*Note*
f = f(t,x) → df = (∂_tf) dt + (∂_xf) dx
f = ∫df = ∫(∂_tf) dt + ∫(∂_xf) dx
f → (∂_tf)∫dt + (∂_xf)∫dx = (∂_tf)*t + (∂_xf)*x {if the partials are constants wrt. t and x, which was the condition from A not being a function of X}
This comes up in the SR Phase and SR Analytic Mechanics.

Thus:
Θ can be up to first order in X
A = ∂[Θ] can only be constant wrt. X
∂[A] being zero wrt. X
This all leads into Choice of Gauge/Gauge-Fixing, where a term proportional to ∂[A] can be added, since it is basically adding a "zero".

X = ∂[(cτ)²]/2, where (cτ)² = (ct)² - x·x = X·X

Tensor Invariants
===========================================================
(0,0)-Tensor = Lorentz Scalar S: Has either (0) or (1) Tensor Invariant, depending on exact meaning
(S) itself is Invariant

(1,0)-Tensor = 4-Vector V^μ: Has (1) Tensor Invariant
V∙V = V^μη_μνV^ν = η_μνV^μV^ν = Tr[V^μV^ν] = V_νV^ν = (v₀v⁰ + v₁v¹ + v₂v² + v₃v³) = (v⁰v⁰ - v∙v) = (v⁰_o)² = Lorentz Scalar Product

(2,0)-Tensor = 4-Tensor T^μν: Has (4) Tensor Invariants
a) T^α_α = Trace
b) T^α_[αT^β_β] = Asymm Bi-Product → Inner Product
c) T^α_[αT^β_βT^γ_γ] = Asymm Tri-Product → ?Name?
d) T^α_[αT^β_βT^γ_γT^δ_δ] = Asymm Quad-Product → Determinant

eg. T^α_[αT^β_β] = T^α_αT^β_β - T^α_βT^β_α = (T^γ_γ)² - T^α_βT^β_α{1} = (T^γ_γ)² - T^α_βT^β_α{(¼)η_γδη^γδ}
and, bending tensor rules slightly: = (T^γ_γ)² - T^α_βT^β_α{(¼)η_βδη^βδ} = (T^γ_γ)² - T^α_β(η^βδ)T^β_α(η_βδ){(¼)} = (T^γ_γ)² - T^αδT_δα{(¼)}
and, since linear combinations of invariants are invariant:
Examine just the (T^αδT_δα) part, which for symm|asymm is (±)(T^αδT_αδ) ie. the InnerProduct Invariant

a): Trace[T^μν] = Tr[T^μν] = η_μνT^μν = T_ν^ν = (T₀⁰ + T₁¹ + T₂² + T₃³) = (T⁰⁰ - T¹¹ - T²² - T³³) = (T)
eg. Faraday Trace[F^μν] = (0 - 0 - 0 - 0) = 0
b): InnerProduct T_μνT^μν = T₀₀T⁰⁰ + {T_i0Tⁱ⁰ + T_0jT^0j} + T_ijT^ij = (T⁰⁰)² - Σ_i[Tⁱ⁰]² - Σ_j[T^0j]² + Σ_i,j[T^ij]²
for symmetric | anti-symmetric: = (T⁰⁰)² - 2Σ_i[Tⁱ⁰]² + Σ_i,j[T^ij]² = Σ_μ=ν[T^μν]² - 2Σ_i[Tⁱ⁰]² + 2Σ_i>j[T^ij]²
eg. Faraday F_μνF^μν = Σ_μ=ν[F^μν]² - 2Σ_i[Fⁱ⁰]² + 2Σ_i>j[F^ij]² = (0) - 2(e∙e/c²)+ 2(b∙b) = 2{(b∙b)-(e∙e/c²)}
c): Antisymmetric Triple Product T^α_[αT^β_βT^γ_γ]
If I got all the math right: T^α_[αT^β_βT^γγ_] = Tr[T^μν]³ - 3(Tr[T^μν])(T^α_βT^β_α) + T^α_βT^βγT^γ_α + T^αγT^β_αT^γ_β
eg. Faraday Asymm Tri-Product = F^α_[αF^β_βF^γγ_] = Tr[F^μν]³ - 3(Tr[F^μν])(F^α_βF^β_α) + F^α_βF^β_γF^γ_α + F^α_γF^β_αF^γ_β = (0) - 3(0)(F^α_βF^β_α) + F^α_βF^β_γF^γ_α + F^α_γF^β_αF^γ_β = F^α_βF^βγ(-F^α_γ) + F^α_γ(-F^α_β)(-F^β_γ) = 0
d): Determinant Det[T^μν] =?= -(1/2)ϵ_αβγδT^αβT^γδ
for anti-symmetric: Det[T^μν] = Pfaffian[T^μν]²
eg. Faraday Det[F^μν] = Pfaffian[F^μν] = (-e^x/c)(-b^x) - (-e^y/c)(b^y) + (-e^z/c)(-b^z) = (e^xb^x/c) + (e^yb^y/c) + (e^zb^z/c) = (e·b)/c

Importantly, the Faraday EM Tensor has only (2) linearly-independent invariants, 2{(b∙b)-(e∙e/c²)} & {(b∙e)/c}²
F^αβ=∂^αA^β-∂^βA^α : The 4-Gradient and 4-EMVectorPotential have 4 independent components each, for total of 8.
Subtract 2 for the 2 Faraday invariants to get total of 6 independent components = 6 independent components of a 4x4 antisymmetric tensor
= 3 electric (e) + 3 magnetic (b) = 6 independent EM field components

Other accounts that I read say:
---
Examples of tensor invariants are:
The (n) eigenvalues
The determinant
The trace
The inner and outer products
However, these are not all independent
A symmetric 2nd-order tensor always has (3) independent invariants, but I am not sure if this is a general statement, or just for 3x3 tensors
---

Basis Representation & Independence (Manifest Covariance):
===========================================================
In standard 3-vector physics, there are several coordinate systems that one can choose:

Basis	3-position Representation	_Lower Metric g_ij	^Upper Metric g^ij	Line Element dx·dx = dxⁱg_ijdx^j = (dl)²
Euclidean Space Independent	x	η_ij	η^ij	(dl)² = dx·dx = dxⁱη_ijdx^j
Euclidean Cartesian/Rectangular	x→(x,y,z)	η_ij → Diag[+1,+1,+1] = δ_ij = I	η^ij → Diag[+1,+1,+1]	(dl)² = dx² + dy² + dz²
Euclidean Cylindrical/Polar	x→(r,θ,z)	η_ij → Diag[+1,+r²,+1]	η^ij → Diag[+1,+1/r²,+1]	(dl)² = dr² + r²dθ² + dz²
Euclidean Spherical	x→(r,θ,φ) x→(r,{Ω})	η_ij → Diag[+1,+r²,+(r·sin[θ])²]	η^ij → Diag[+1,+1/r²,+1/(r·sin[θ])²	(dl)² = dr² + r²dθ² + (r·sin[θ])²dφ² (dl)² = dr² + r²dΩ²

When the components of the 4-Vector { A }are in (time scalar,space 3-vector) form { (a⁰,a) }, then the 4-Vector is in spatial basis invariant form.
Once you specify the spatial components, you have picked a basis or representation. I indicate this by using { → }.
These can all indicate the same 4-Vector, but the components of the 4-Vector will vary in the different bases.
Minkowski Space is a pseudo-Euclidean Space

Basis	4-Position Representation	_Lower Metric g_μν	^Upper Metric g^μν	WorldLine Element dX·dX = dX^μg_μνdX^ν = (cdτ)²
Minkowski SpaceTime Independent	X	η_μν	η^μν	(cdτ)² = dX·dX = dX^μη_μνdX^ν
Minkowski Time-Space	X→(ct,x)	η_μν → Diag[+1,-I]	η^μν → Diag[+1,-I]	(cdτ)² = (cdt)² - dx·dx
Minkowski Cartesian/Rectangular	X→(ct,x,y,z)	η_μν → Diag[+1,-1,-1,-1]	η^μν → Diag[+1,-1,-1,-1]	(cdτ)² = (cdt)² - dx² - dy² - dz²
Minkowski Cylindrical/Polar	X→(ct,r,θ,z)	η_μν → Diag[+1,-1,-r²,-1]	η^μν → Diag[+1,-1,-1/r²,-1]	(cdτ)² = (cdt)² - dr² - r²dθ² - dz²
Minkowski Spherical	X→(ct,r,θ,φ) X→(ct,r,{Ω})	η_μν → Diag[+1,-1,-r²,-(r·sin[θ])²]	η^μν → Diag[+1,-1,-1/r²,-1/(r·sin[θ])²	(cdτ)² = (cdt)² - dr² - r²dθ² - (r·sin[θ])²dφ² (cdτ)² = (cdt)² - dr² - r²dΩ²
others...
Newtonian Gravity Cartesian/Rectangular {weak gravity limiting-case \|φ\|<<1} {becomes Minkowski for φ→0}	X→(ct,x,y,z)	g_μν → Diag[+(1+2φ),-1,-1,-1]	g^μν → Diag[+1/(1+2φ),-1,-1,-1]	(cdτ)² = (1+2φ)(cdt)² - dx² - dy² - dz²
Schwartzschild Spherical {becomes Minkowski for R_S→0 or r→∞}	X→(ct,r,θ,φ)	g_μν → Diag[+(1-R_S/r),-1/(1-R_S/r),-r²,-r²sin(θ)]	g^μν → Diag[+1/(1-R_S/r),-(1-R_S/r),-1/r²,-1/r²sin(θ)]	(cdτ)² = (1-R_S/r)(cdt)² - 1/(1-R_S/r)dr² - r²dθ² - (r·sin[θ])²dφ²
FLRW (or FRW) Spherical {assumes homogeneity & isotropy} a[t] is "scale factor" k is uniform curvature constant typically k={-,0,+}	X→(ct,r,θ,φ)	g_μν → Diag[+1,1/(a[t])²{-1/(1-kr²),-r²,-(r·sin[θ])²}]	g^μν → Diag[+1,(a[t])²{-(1-kr²),-1/r²,-1/(r·sin[θ])²}]	(cdτ)² = (cdt)² - (a[t])²{1/(1-kr²)dr² + r²dθ² + (r·sin[θ])²dφ²} (cdτ)² = (cdt)² - (a[t])²{1/(1-kr²)dr² + r²dΩ2} (cdτ)² = (cdt)² - (a[t])²{dΣ²}

with Spherical Surface Element dΩ² = dθ² + (sin[θ])²dφ²
with Reduced-Circumference Element dΣ² = 1/(1-kr²)dr² + r²dΩ2, with Σ ranging over 3D space of uniform curvature {elliptical, Euclidean, hyperbolic}
with Curvature k
with Schwartzschild Radius R_S = (2MG)/c²

η_ανη^νβ = η_α^β = δ_α^β = Diag[1,1,1,1]
η_αβη^αβ = Tr[η^αβ] = δ_α^α = δ_β^β = 4
[η^μμ] = 1/[η_μμ], and all non-diagonal components = 0
[η^μν] = δ^μν/(1 - δ_μν + [η_μν]) = 1/[η_μν] for {μ = ν}; 0 for {μ ≠ ν}

Now, once you are in a space basis invariant form, eg. X = (ct,x), you can still do a Lorentz boost and still have the same 4-Vector X.
It is only when using 4-Vectors directly, (eg. X·Y, X+Y), that you have full SpaceTime Basis Independence.
Knowing this, we want to try to find as many relations as possible in 4-Vector and Tensor format, as these are applicable to all observers.

Ageing along a WorldLine:
Generally Δτ = ∫dτ
Minkowski Δτ = ∫dτ = (1/c)∫√[(cdt)² - dx² - dy² - dz²] = (1/c)∫√[(c)² - ẋ² - ẏ² - ż²]dt = (1/c)∫√[c² - u²]dt = ∫√[1 - β²]dt = ∫dt/γ
Newtonian Δτ = ∫dτ = (1/c)∫√[(1+2φ)(cdt)² - dx² - dy² - dz²] = (1/c)∫√[(1+2φ)(c)² - ẋ² - ẏ² - ż²]dt = (1/c)∫√[(1+2φ)c² - u²]dt = ∫√[(1+2φ) - β²]dt ≈ ∫(1 +φ -β²/2 + ...)dt
with the final approx. (≈) Newtonian result for |φ|<<1 and |β|<<1

One can interpret this as ageing rate decreases when you move faster (-β²/2) but ageing rate increases as you move higher up a "potential" (+φ)

Standard Physical SR 4-Vectors

I will introduce the SR Physical 4-Vectors, which encapsulate the Physical Properties of Nature.
I will show how these SR 4-Vectors are related to one another in purely relativistic theory, i.e. the Physical Laws of Nature.
Consider the following Physical SR 4-Vectors {which are (1,0)-Tensors}:
========================================================================
4-Position R = R^μ = (ct,r) → (ct,r,θ,z) or (ct,r,θ,φ); X = X^μ = (ct,x) → (ct,x,y,z)
4-Velocity U = U^μ = (U⁰,Uⁱ) = γ(c,u)
4-Acceleration A = A^μ = (A⁰,Aⁱ) = γ(cγ̇,γ̇u + γu̇) = γ(cγ̇,γ̇u + γa)
4-Differential dR = dR^μ = (cdt,dr); dX = dX^μ = (cdt,dx)
4-Displacement ΔR = ΔR^μ = (cΔt,Δr); ΔX = ΔX^μ = (cΔt,Δx)
4-Momentum P = P^μ = (E/c,p) = (mc,p)
4-MomentumDensity G = G^μ = (E_den/c,p_den) = (u_e/c,g)
4-Force F = F^μ = (F⁰,Fⁱ) = γ(Ė/c,ṗ) = γ(Ė/c,f) = γ(ṁc,f)
4-ForcePure F_p = F_p^μ = γ(u·f/c,f)
4-Force_EM F_EM = F_EM^μ = γq( (u·e)/c, (e) + (u⨯b) )
4-ForceHeat F_h = F_h^μ = γṁ(c,u) = γ²ṁ_o(c,u)
4-ForceScalar F_s = F_s^μ = k(∂_t[Φ],-∇[Φ])
4-ForceDensity F_den = F_den^μ = γ(Ė_den/c,f_den)
4-NumberFlux N = N^μ = N_f = n(c,u) = (cn,nu) = (cn,n) = Σ_a[∫dτ δ⁽⁴⁾[X - X_a(τ)]dX_a/dτ]
4-EntropyFlux S = S^μ = s(c,u) = (cs,su) = (cs,s)
4-CurrentDensity J = J^μ = ρ(c,u) = (cρ,ρu) = (cρ,j)
4-VectorPotential A = A^μ = (φ/c,a) = A[X] = A[(ct,x)] = (φ[(ct,x)]/c,a[(ct,x)]), often used for/as A_EM
4-PotentialMomentum Q = Q^μ = (U/c,q) = q(φ/c,a)
4-TotalMomentum P_T_particle = P_Tparticle^μ = (E_T/c,p_T) = (H/c,p_T) = (E/c + U/c,p + q) = (E/c + qφ/c,p + qa), meaning the sum of particle momentum and charged interaction potential momentum
4-TotalMomentum P_T_sys = P_Tsys^μ = (E_T/c,p_T) = (H/c,p_T) = Σ_n[P_T_particle(n)], meaning that the total 4-Momentum of a system is the sum of all individual particle 4-Momenta in the system
4-WaveVector K = K^μ = (ω/c,k) = (ω/c,n̂ω/v_phase) = (ω/c,ωu/c²) = (ω/c)(1,β) = (1/cT,n̂/λ)
4-CyclicWaveVector K_cyc = K_cyc^μ = (ν/c,k_cyc) = (ν/c,n̂ν/v_phase) = (ν/c,νu/c²) = (ν/c)(1,β) = (1/cT,n̂/λ)
4-TotalWaveVector K_Tsys = K_Tsys^μ = (ω_T/c,k_T) = Σ_n[K_T_wave(n)], meaning that the total 4-WaveVector of a system is the sum of all the individual 4-WaveVectors in the system
4-DifferentialWaveVector dK = dK^μ = (dω/c,dk)
4-Gradient ∂ = ∂^μ = ∂_X = (∂_t/c,-∇) = (∂_t/c,-del) → (∂_t/c, -∂_x, -∂_y,-∂_z) = (∂/c∂t,-∂/∂x,-∂/∂y,-∂/∂z)
4-WaveGradient ∂_K = ∂_K^μ = (c∂_ω,-∇_k) = (c∂_ω,- del_k) → (c∂_ω, -∂_kx, -∂_ky,-∂_kz) = (c∂/∂ω,-∂/∂k_x,-∂/∂k_y,-∂/∂k_z)
4-Polarization Ε = Ε^μ = (ε⁰,ε) → (ε·β,ε), with (ε·β = 0) *Note* this can have complex coefficients, and comes from standard EM theory (non-QM), see Jones Vector
I choose this particular set because each of these is considered a basic SR 4-Vector, meaning that no QM axioms are required for the definition of these 4-Vectors.
There will be some more Physical 4-Vectors added later...

To this list I will add some Mathematical 4-Vectors:
=====================================================
4-Zero = Z = Z^μ = (0,0) = 0^μ
4-UnitTemporal T = T^μ = γ(1,β)
4-UnitSpatial S = S^μ = γ[β_n̂] (n̂·β,n̂) with (n̂ any direction) or S = (n̂·β,n̂) with ({n̂·β = 0} = n̂⊥β = n̂ orthogonal-to β)
4-Null N = N^μ = I_n(1,n̂)
4-UnitHyperSurfaceNormal N = N^μ = (n⁰,n) with (N·N) = {1 for time-like, 0 for light-like, -1 for space-like}
These are handy for purely mathematical operations, as each of these are physically dimensionless.

These 4-Vectors, or their variations, may found in the texts on Relativity, Special Relativity, and Classical Electromagnetism.
I particularly like the texts by physicist Wolfgang Rindler, noted for his work and contributions to the field of Relativity.
*Note* The 4-Polarization can be found in Rindler's "Introduction to Special Relativity, 2nd Ed." in Section 43-Electromagnetic Waves,
as well as some other texts on Classical Electrodynamics, eg. Jackson.

Note that each 4-Vector consists of a temporal component, and a spatial component.
Also, just a quick tangent, I ran across an interesting internet meme epiphany on a website:
"Art is how we decorate space, music is how we decorate time" - Thought provoking... 4-Decoration = (music / c, art). Pretty cool :)

====================================================
We will also see a few SR 4-Tensors, usually (2,0)-Tensors, each of which can be built up from the SR Physical 4-Vectors, which are themselves (1,0)-Tensors.
Notation:
4-Scalar, no index, created from contractions of higher index 4-Vectors & 4-Tensors
4-Vector, the index has 4 values, running from 0..3
4-Tensor, each index has 4 values, independently running from 0..3

Tensor Type	Representation	Index Type	^Upper Index Count	_LowerIndex Count	Alt Name	Further Definitions
(0,0)-Tensor	S	N/A	0	0	(Lorentz) (4-)Scalar	Invariant component
(1,0)-Tensor (0,1)-Tensor	V^μ V_μ	Contravariant Covariant	1 0	0 1	4-Vector 4-Covector	1 temporal, 3 spatial components
(2,0)-Tensor (1,1)-Tensor (0,2)-Tensor	T^μν T^μ_ν or T_μ^ν T_μν	Contravariant Mixed Covariant	2 1 0	0 1 2	4-Tensor	1 temporal, 9 spatial, 6 mixed time-space components Independent Components: Symmetric: 10 Anti-Symmetric: 6 Generic: 16 possible

4-Scalar S

4-Vector V^μ

V⁰

V¹

V²

V³

4-Tensor T^μν

T⁰⁰	T⁰¹	T⁰²	T⁰³
T¹⁰	T¹¹	T¹²	T¹³
T²⁰	T²¹	T²²	T²³
T³⁰	T³¹	T³²	T³³

{The temporal region in blue, the spatial region in red, the mixed time-space regions in purple}

Often, the tensor-index notation is required to reduce any ambiguity.
Also, remember that these are SR (flat SpaceTime), and modifications are required for GR curvature effects
(mainly using g^μν instead of η^μν, and using a covariant derivative: comma to semi-colon rule {(,) → (;)} where V^μ_;ν = V^μ_,ν + V^αΓ^μ_αν).
see Minkowski Metric, Faraday Tensor, Stress-Energy Tensor, EM Stress-Energy Tensor, Relativistic Angular Momentum,
I put these in green because every Physical SR Tensor seems to be composed of more basic Physical SR 4-Vectors.

Standard Physical SR 4-Tensors

Consider the following Physical SR 4-Tensors {which are mostly (2,0)-Tensors, and using the (+---) convention}:
=======================================================================
Minkowski Metric Tensor η^μν = ∂^μ[X^ν] = Diag[+1,-1,-1,-1] {in Cartesian frame}; η_μν = Diag[+1,-1,-1,-1] = ( ^μ)·( ^ν) = Trace[ ^μν] = Tr[ ^μν]; [η^μν] = 1/[η_μν] for {μ = ν}; 0 for {μ ≠ ν}

Electromagnetic (EM) Tensors: Anti-Symmetric (Light-Like)
Faraday EM Field Tensor F^μν = (∂^μA_EM^ν - ∂^νA_EM^μ)
Magnetization-Polariztion Tensor M^μν
EM Displacement Tensor D^μν
EM Dipole Tensor σ^μν
see 4-Tensors,

Stress-Energy Tensors T^μν: Symmetric
T_GRvacuum^μν = 0
T_{relativisticfluid}^μν = (ρ_eo)V^μν - (p_o)H^μν + (T^μQ^ν + Q^μT^ν) + Π^μν
T_perfectfluid^μν = (ρ_eo + p_o)U^μU^ν/c² - (p_o)η^μν = (ρ_eo + p_o)T^μT^ν - (p_o)η^μν = (ρ_eo)T^μT^ν - (p_o)H^μν = (ρ_eo)V^μν - (p_o)H^μν
   T_dust^μν = (ρ_eo)U^μU^ν/c² = (ρ_eo)T^μT^ν = (ρ_eo)V^μν
   T_vacuum^μν = -(p_o)η^μν = (ρ_eo)η^μν
   T_{radiation = nulldust}^μν = p_o(4U^μU^ν/c² - η^μν) = p_o(4T^μT^ν - η^μν) = p_o(4V^μν - η^μν) = (ρ_eo)[V^μν - (1/3)H^μν] = (ρ_eo)N^μν
T_{EM = photongas}^μν = (1/μ_o)(F^μαη_αβF^νβ - η^μνF_δγF^δγ/4)

Relativistic Angular Momentum (Pseudo-)Tensor M^μν = (X^μP^ν - X^νP^μ) = X^μ ^ P^ν = 2(X^[μP^ν]) = {sometimes written as L^μν}
Relativistic Total Angular Momentum Tensor M_T^μν = Σ_n[M_(n)^μν], {meaning the Total AM is the sum of all individual AM, sometimes written as J^μν}
Relativistic Torque (4-Couple) Tensor G^μν = (X^μF^ν - X^νF^μ) = X^μ ^ F^ν = d/dτ[M^μν] = {sometimes written as N^μν}
Relativistic 4-Spin S^μ = (1/2)ε^μ_νρσM_T^νρU^σ, {The Pauli-Lubanski 4-Spin: *note* does not require a quantum assumption to construct from SR 4-Vectors}
Relativistic 4-SpinMomentum W^μ = (1/2)ε^μ_νρσM_T^νρP^σ, {The Pauli-Lubanski 4-Spin: *note* does not require a quantum assumption to construct from SR 4-Vectors}
   where W^μPμ = 0
The 4-Spin is an angular momentum that is independent of the pivot, or the intrinsic angular momentum.
It is a 4-Vector, but I put here due to its complicated formulation and relation to the Angular Momentum Tensor.
see Stern-Gerlach Experiment,

Gravitational Wave Tensor h^μν
Technically this is a "perturbation" on the Minkowski Metric, where the "flat SpaceTime limiting case" of gravitational waves act like plane waves in the SpaceTime manifold.
g^μν = η^μν + h^μν where |h^μν| << 1

There are some mathematical (2,0)-Tensors also, again made up from individual 4-vectors.
=======================================================================
SpaceTime Projection Tensor (Minkowski Metric) η^μν = V^μν + H^μν = ∂^μ[X^ν]
Temporal Projection Tensor V^μν = T^μ⊗T^ν = T^μT^ν = U^μU^ν/c²: Also known as the (V)ertical or tangential projection tensor
Spatial Projection Tensor H^μν = S^μ⊗S^ν = η^μν - V^μν = η^μν - T^μT^ν = η^μν - U^μU^ν/c²: Also known as the (H)orizontal or normal or orthogonal projection tensor
Diagonal Projection Tensor D₁^μν = T^μ⊗S^ν = T^μS^ν: The 1st (D)iagnol projection tensor???
Diagonal Projection Tensor D₂^μν = S^μ⊗T^ν = S^μT^ν: The 2nd (D)iagnol projection tensor???
Null (Unit) Projection Tensor N^μν = N^μ⊗N^ν = N^μN^ν = V^μν - (1/3)H^μν
The Kronecker Delta 4-Tensor = δ_μ^ν = ∂_μX^ν = η_μ^ν = η_μαη^αν: (1 if μ = ν; 0 if μ ≠ ν; μ,ν = [0..3]) {also the LorentzTransform*InverseLorentzTransform (Λ^ρ_ν'Λ^ν'_β) = δ^ρ_β}
The Kronecker Delta 3-tensor = δ_j^k: (1 if j = k; 0 if j ≠ k; j,k = [1..3])
The Levi-Civita (Cyclic Permutation) 4-Tensor = ε^μνρσ, (1 if even permutation; -1 if odd permutation; 0 if no permutation; totally anti-symmetric; [0..3])
The Levi-Civita (Cyclic Permutation) 3-tensor = ε^ijk, (1 if even permutation, -1 if odd permutation, 0 if no permutation; totally anti-symmetric; [1..3])
The 3-tensor form of Levi-Civita can be used to make 3-vectors from an Anti-Symmetric (2,0)-Tensor
eg. b^k = -(1/2)ε_ij^kF^ij = (b¹,b²,b³) = (F²³,F³¹,F¹²): Magnetic Field b

ε^ijkε_klm = δⁱ_lδ^j_m - δⁱ_mδ^j_l
ε^ijkε_jkl = 2δⁱ_l
ε^ijkε_ijk = 6

Since the Levi-Civita is non-zero only when all indices are different:
ε¹²³ε₁₂₃ = (1)(1) = 1 and ε¹³²ε₁₃₂ = (-1)(-1) = 1
ε²³¹ε₂₃₁ = (1)(1) = 1 and ε²¹³ε₂₁₃ = (-1)(-1) = 1
ε³¹²ε₃₁₂ = (1)(1) = 1 and ε³²¹ε₃₂₁ = (-1)(-1) = 1
Summing all gives 6

*Note* Temporarily using Latin indices i,j,k,l from [0..3] just for the Minkowski Levi-Civita (because most examples I can find do this)
I will fix this later into Greek index notation once I understand tensor-densities better.
ε⁰¹²³ = 1 and e^ijkl = (-1)^m where m = # of permutations required to bring e^ijkl into ε⁰¹²³, and zero otherwise
ε₀₁₂₃ = -1 and e_ijkl = (-1)^{(m + 1)} where m = # of permutations required to bring e_ijkl into ε₀₁₂₃, and zero otherwise

ε^ijklε_mnpq = -24( δ_m^[iδ_n^jδ_p^kδ_q^l])

ε^ijklε_mnpq = -det[matrix]
|δ_mⁱ, δ_nⁱ, δ_pⁱ, δ_qⁱ|
-|δ_m^j, δ_n^j, δ_p^j, δ_q^j|
|δ_m^k, δ_n^k, δ_p^k, δ_q^k|
|δ_m^l, δ_n^l, δ_p^l, δ_q^l|

ε^ijklε_mnpl = -det[matrix]
|δ_mⁱ, δ_nⁱ, δ_pⁱ |
-|δ_m^j, δ_n^j, δ_p^j |
|δ_m^k, δ_n^k, δ_p^k|

ε^ijklε_mnkl = -det[matrix]
-2|δ_mⁱ, δ_nⁱ| = 2(δ_mⁱδ_n^j - δ_nⁱδ_m^j)
|δ_m^j, δ_n^j|

ε^ijklε_mjkl = -3!1!(δ_mⁱ) = -6(δ_mⁱ)

ε^ijklε_ijkl = -4! = -24

The 4-Tensor form of Levi-Civita can be used to make 4-Vectors from an Anti-Symmetric (2,0)-Tensor combined with the 4-Velocity
eg. S^μ = (1/2)ε^μ_νρσM_T^νρU^σ = (1/2)η^μαε_ανρσM_T^νρU^σ, {The Pauli-Lubanski 4-Spin: *Note* Does not require a quantum assumption to construct from SR 4-Vectors}

Standard Physical SR 4-Vector References

Now, just to have a reference of where some of these SR objects come from...
========================================
Wolfgang Rindler, Intro. to Special Relativity, 2nd Ed.
4-Vectors and Lorentz Scalars
========================================
4-TensorMinkowskiMetric: pg.51,159
LorentzScalarGeneric: pg.51
4-VectorInterval: pg.51
4-Position: pg.56
4-Differential/Displacment: pg.56,62,154
4-TimeLike: pg.57
4-SpaceLike: pg.57
4-Null: pg.57
4-Velocity: pg.58
4-Acceleration: pg.59
4-WaveVector/4-Frequency: pg.62,82,122
LorentzScalar Phase: pg.63
4-Zero: pg.66
4-Momentum: pg.71
4-TotalMomentum(sum of particles): pg.78
4-TensorAngularMomentum(sum of AM's): pg.87
4-TotalTensorAngularMomentum: pg.87
4-Spin(Pauli-Lubanski)/IntrinsicAngularMomentum: pg.89
4-TotalTensorAngularMomentum(regular + intrisic): pg.90
4-Force: pg.90
4-Force(Heat): pg.92
4-Force(Scalar): pg.92
4-Force(Pure): pg.93
4-Force(EM): pg.94
4-VectorPotential/Potential: pg.95,107
4-TotalMomentum(intrinsic + potential): pg.95
LorentzScalar Action: pg.96
4-DeltaDisplacement: pg.99
4-TensorTorque/4-Couple: pg.100
4-TensorFaraday: pg.103
4-CurrentDensity: pg.103,106
4-TensorFaradayDual: pg.103
4-TensorLevi-CivitaAntiSymmetric/4DPermutation: pg.108,162-163
4-MagneticCurrentDensity = 0: pg.110
4-Gradient/ProperTimePartial: pg.94,113,155,157
4-KroneckerDelta: pg.113,153
4-RetardedDisplacement: pg.113
4-RetardedVelocity: pg.114
4-NumberFlux(by implication): pg.118 - try instead "Schutz, A 1st Course in GR", pg.90
4-ForceDensity: pg.118
4-EMEnergyStressTensor: pg.119
4-MomentumDensity: pg.121,138
4-Polarization: pg.122
4-WaveFunctionVector/WavePotential: pg.122
4-RadiationDust/PhotonGasEnergyStressTensor: pg.124,127,141
4-GenericEnergyStressTensor: pg.130
4-TotalEnergyStressTensor: pg.132
4-PerfectFluidEnergyStressTensor: pg.140
4-DustEnergyStressTensor: pg.140
4-ArbitraryDifferentiableVector: pg.142
4-UnitOutwardNormalVector: pg.142
4-ArbitraryConstantVector: pg.143
4-TensorZero: pg.154
4-SymmetricTensor: pg.161
4-AntiSymmetricTensor: pg.161
4-UnitTemporal/Tangent: pg.162
4-UnitSpatial/PrincipleNormal: pg.162
=========================================

Standard Physical SR 4-Vector Properties

4-Position R = (ct,r); X = (ct,x)
X = (1/2)∂[(cτ)²]
gives the location of an event in SpaceTime: SI Units [m].
Typically this would be the location of an SR particle.
( t ) is the temporal location and ( r ) or ( x ) the spatial location.
The Lorentz Scalar Product R·R = (ct)² - r·r = (ct)² - |r|²
R·R = (ct_o)² = (cτ)² > 0 {for time-like separation (+)interval}
R·R = 0 {for light-like separation (0)interval = Null/Photonic}
R·R = -(|r_o|²) < 0 {for space-like separation (-)interval}
gives the invariant distance or interval or measure between events,
using the (t0+ℝ) SR metric sign convention.
When the spatial part r is 0, this gives a Lorentz invariant rest time t_o = τ = Proper Time.
Relativistic time t = γt_o = γτ.
( x ) is typically used when talking about Cartesian systems, and ( r ) for systems with a radial or spherical symmetry.
The 4-Position is invariant only under rotations and boosts about the origin (Lorentz Invariant),
unlike the 4-Displacement, which is invariant under both general rotations/boosts and translations (Poincaré Invariant).
The reason for this is that the 4-Position is a 4-Displacement that has one of its events "pinned" to the origin (i.e. one of them is the 4-Zero).
A translation would break the "pinning".
Interestingly, X = (1/2)∂[(cτ)²]: The 4-Position can be seen as a gradient of the ProperTime squared.
R = ∂[(cτ)²]/2, where (cτ)² = (ct)² - r·r
=============================

4-Velocity U = U^μ = (U⁰,Uⁱ) = (γc,γu) = γ(c,u)= γ(c,v) = γc(1,β)
U = dR/dτ = (U·∂)[R]
U = dX/dτ = (U·∂)[X]
U = cT
U = c²∂[τ]
gives the motion of an event in SpaceTime: SI Units [m/s].
Typically this would be the motion of an SR particle.
( γ ) is the SR Lorentz gamma factor { γ = 1/√[1-β²]; β = u/c }, ( c ) is the temporal velocity, ( u ) or ( v ) is the spatial velocity.
The Lorentz Scalar Product U·U = γ(c,u)·γ(c,u) = γ²(c,u)·(c,u) = γ²(c² - u·u) = c²γ²(1 - β·β) = (c)²
says that all SR events (massive or massless) have invariant 4-Velocity magnitude of (c) in the temporal direction.
This is despite the fact that for massless particles the 4-Velocity goes Infinite (and thus not well-defined) in the null-direction { U_c = Infinite(c,cn̂) }
When the spatial part ( u ) is 0, this gives a Lorentz invariant rest temporal velocity c.
All stationary worldlines race into the future at the speed of light (c).
see the "Invariant Rest Value of the Temporal Component Rule"
Interestingly, the 4-Velocity has only 3 independent components, unlike the other SR 4-Vectors here, which typically have 4 independent components.
The reason for this is the constraint imposed by the Lorentz Scalar Product.
Since U·U = (c)² is a universal constant, this lowers the number of degrees of freedom by 1, leaving only 3 independent components.
This is actually quite handy, as multiplication by certain other Lorentz Scalars allows the result to have 4 independent components.
Thus, several 4-Vectors are actually just Lorentz Scalar multiples of the 4-Velocity. (eg. P = m_oU and J = ρ_oU )
In a rest frame, U → U_o = (c,0)
If we then apply an Inverse Lorentz Transform: U^β' = Λ^β'_αU_o^α = γ[[1 β],[β 1]](c,0) = γ([1*c + β·0],[β*c + 1*0]) = γ([c + 0],[u + 0]) = γ(c,u) = U

SRQM 4-Vector : Four-Vector Motion of Lorentz Scalar Invariants

SRQM 4-Vector : Four-Vector Motion of Lorentz Scalar Invariants

=============================

4-Acceleration A = (A⁰,Aⁱ) = γ(cγ̇ , γ̇u + γu̇) = γ(cγ̇ , γ̇u + γa)	= ( γ⁴(a·u)/c , γ⁴(a·u)u/c² + γ²a )	= γ⁴( (a·u)/c , a + u x (a x u)/c² )
	= ( γ⁴(a·β) , γ⁴(a·β)β + γ²a )	= γ⁴( (a·β) , a + β x (a x β) )
	= γ⁴( (a·β) , (a·β)β + a/γ² )

A = dU/dτ = (U·∂)[U]
gives the acceleration of an event in SpaceTime: SI Units [m/s²].
Typically this would be the acceleration of an SR particle.
( γ ) is the SR Lorentz gamma factor { γ = 1/√[1-β²]; γ̇ = dγ/dt = γ³uu̇/c² = γ³ββ̇; β = u/c }, ( c ) is the temporal velocity, ( u ) is the spatial velocity, ( a = u̇ ) is the spatial acceleration.
** Take care not to confuse with the 4-VectorPotential A**
The Lorentz Scalar Product
A·A =
= γ(cγ̇,γ̇u + γu̇)·γ(cγ̇,γ̇u + γu̇)
= γ²[( cγ̇ )² - (γ̇u + γu̇)²]
= γ²[ c²γ̇² - (γ̇²u² + 2γγ̇uu̇ + γ²u̇²) ]
= - [ γ⁶u²u̇²/c² + γ⁴a²) ]
= - γ⁴[a² + (γ/c)²(u·a)²] = - γ⁴[a² + γ²(β·a)²]
= - γ⁶[a² - (u x a)²/c²] = - γ⁶[a² - (β x a)²] = - c²γ⁶[β̇² - (β x β̇)²]
= γ⁶[ (u x a)²/c² - a²) ] = γ⁶[ (β x a)² - a²) ]
= -(a_o²)
= -(α²)
In an instantaneously co-moving reference frame (ICRF), we get A_o = (0,u̇) = (0,a_o) = (0,α)
The Lorentz Scalar Product A_o·A_o = (0,α)·(0,α) = (0² - α·α) = -(|α|²) = -(α²)
says that the 4-Acceleration Magnitude is always spatial.
So, events move temporally/tangentially along their worldlines,
with accelerations acting normally/perpendicularly to bend/curve the worldlines spatially.
An example of the use of the Lorentz Scalar Product A·A is radiated power.
The radiated power P of an accelerated charge:[All in SI units]
P =
= -μ_oq²(A·A)/(6πc)
= -q²(A·A)/(6πε_oc³)
= -(2/3)q²(A·A)/(4πε_oc³)
= -(2/3)q²(dU/dτ·dU/dτ)/(4πε_oc³)
= -(2/3)q²(dP/dτ·dP/dτ)/(4πε_om_o²c³)
= -q²(dP/dτ·dP/dτ)/(6πε_om_o²c³)
= -q²/(6πε_om_o²c³)γ⁶[ (u x a)²/c² - a²) ]
= q²/(6πε_om_o²c³)γ⁶[a² - (u x a)²/c²]
= q²/(6πε_om_o²c³)γ⁶[a² - (β x a)²]
= q²/(6πε_om_o²c)γ⁶[β̇² - (β x β̇)²]
= (2/3)q²/(4πε_om_o²c)γ⁶[β̇² - (β x β̇)²]

see Larmor Formula, Abraham-Lorentz-Dirac Force,
=============================

4-Differential dR = (cdt,dr); dX = (cdt,dx)
dR = d[R]
gives the differential form of the 4-Position: SI Units [m].
( dt ) is the temporal differential and ( dr ) the spatial differential.
The Lorentz Scalar Product dX·dX = (cdt)² - dx·dx = (cdt)² - |dx|² = c²dτ² = ds²
gives the invariant differential distance or interval or measure between infinitesimally close events.
When the spatial part ( dr ) is 0, this gives a Lorentz invariant rest time displacement dt_o = dτ.
Relativistic temporal displacement dt = γdt_o = γdτ.
Used quite often is: (d/dτ) = γ(d/dt)
Basically, the rules of differential calculus still apply to Minkowski SpaceTime.
Also, this is locally true even in GR.
=============================

4-Displacement ΔR = (cΔt,Δr); ΔX = (cΔt,Δx)
ΔR = Δ[R]
gives the displacement from one event to another in SpaceTime: SI Units [m].
( Δt ) is the temporal displacement and ( Δr ) the spatial displacement.
This is just the interval displacement between 4-Position's X₁ and X₂, with ΔX = X₂ - X₁
The Lorentz Scalar Product ΔX·ΔX = (cΔt)² - Δx·Δx = (cΔt)² - |Δx|²
gives the invariant distance or interval or measure between these two events.
When the spatial part ( Δr ) is 0, this gives a Lorentz invariant rest time displacement Δt_o = Δτ = Proper Time Displacement.
Relativistic temporal displacement Δt = γΔt_o = γΔτ.
The 4-Displacement is invariant under both general rotations/boosts and translations (Poincaré Invariant),
unlike the 4-Position, which is invariant only under rotations/boosts about the origin (Lorentz Invariant).
The reason for this is that the 4-Position is a 4-Displacement that has one of its events "pinned" to the origin (i.e. one of them is the 4-Zero).
A translation would break the "pinning".
=============================

4-Momentum P = (E/c,p) = (mc,p)
P = m_oU = (E_o/c²)U {massive case}
P = (mc)N = (E/c)N = (|p|)N {massless = photonic case, |p| is a "momentum intensity", N is a "unit" 4-Null}
*Note* Only the Rest-Scalars are Lorentz Invariant, the Null-Intensities are relativistic and vary according to the observer.
gives the Energy-Momentum content of an SR particle at a particular event: SI Units [kg·m/s].
( E ) is the energy ( = temporal momentum) of the event and ( p ) is the spatial momentum.
The Lorentz Scalar Product P·P = (E/c,p)·(E/c,p) = (E/c)² - p·p = (E_o/c)² = (m_oc)²
gives Einstein's famous Mass-Energy Equation, which is equivalent to [E = mc² = γm_oc²].
The equation is often rearranged as E = ±√[p·pc²+ (m_oc²)²]
When the spatial part ( p ) is 0, this gives a Lorentz invariant rest energy E_o.

Note:
P = m_oU
(P⁰,Pⁱ) = m_o(U⁰,Uⁱ)
(E/c,p) = m_oγ(c,u) = γm_o(c,u) = m(c,u)

The relativistic temporal component (P⁰) = m_o(U⁰)
The Newtonian temporal component (E/c) = m_oγ(c) = γm_o(c) = m(c)

The relativistic spatial component (Pⁱ) = m_o(Uⁱ)
The Newtonian spatial component (p) = m_oγ(u) = γm_o(u) = m(u)

Relativistic mass m = E/c²
Relativistic energy E = γE_o = γm_oc² = mc² = √[(m_oc²)² + (|p|c)²] = √[(E_o)² + (|p|c)²] : All of these are equivalent formulations.
Relativistic 3-momentum p = γm_ou = mu = (E/c²)u = (γE_o/c²)u : All of these are equivalent formulations.

A very useful relativistic identity for this showing these is: (γ² = 1 + γ²β²) and hence (γ = √[1 + γ²β²]), where (β = u/c) and (γ = 1/√[1-β²])
Now just take E_o(γ = √[1 + γ²β²]), which gives E = γE_o = √[(E_o)² + γ²(E_o)²β²] = √[(E_o)² + γ²(E_o)²(|u|/c)²] = √[(E_o)² + γ²(m_oc²)²(|u|/c)²] = √[(E_o)² + (γm_o|u|c)²] = √[(E_o)² + (|p|c)²]
Interesting limiting-cases are:
Rest Case: |u|→0, γ→1, |p|→0, then E→E_o = m_oc², m→m_o{for rest/time-like} P = (E/c,p) = (mc,p)
Photonic Case: |u|→c, γ→∞, m_o→0, E_o→0, then E = mc²→|p|c; p = ±mc {for null/light-like} P = (|p|,p) = |p|(1,n̂)
(|p|)N = lim[P = m_oU; as m_o→ 0,|u|→ c]
If P·U = 0 = m_oU·U = m_oc², then m_o = 0
If m_o = 0, then P·U = m_oU·U = m_oc² = 0
Thus, {P·U = 0} ↔ {m_o = 0}

Relativistic Mass {m = γm_o}
Relativistic Momentum {p = γm_ov}
Relativistic Kinetic Energy {E_k = E - E_o = (γ-1)m_oc²)}

The Conservation of 4-Momentum unites the Conservation of Energy and Conservation of 3-momentum into a single law,
and plays a major role in just about all physical effects.
P = P_T - qA : Related to the 4-TotalMomentum of a system which can include the effects of a 4-VectorPotential A
P = -∂[S] - qA : Related to the 4-Gradient of the action (S) of a system
=============================

4-MomentumDensity P_den = (E_den/c,p_den) = (m_denc,p_den)
4-MassFlux P_den = (E_den/c,p_den) = (m_denc,p_den)
P_den = (m_o/V_o)U = (E_o/V_oc²)U
P_den = G = n_oP = n_om_oU = m_oN = (n_oE_o/c²)U = ρ_moU = U_νT^μν/c²
gives the Energy-MomentumDensity content of an SR particle/distribution at a particular event: SI Units [kg/m²·s].
( E_den = u_e = e = ε = ρ_e ) is the energy_density ( = temporal momentum_density) of the event,
( m_den = u_m = ρ_m ) is the mass_density,
( p_den = g ) is the spatial momentum_density ( = energy flux).
=============================

4-Force F = (F⁰,Fⁱ) = γ(Ė/c,ṗ) = γ(Ė/c,f) = γ(ṁc,f)
F = dP/dτ = (U·∂)[P] = (d/dτ)[P] = (d/dτ)[m_oU] = (d/dτ)[m_o]U + m_o(d/dτ)[U] = (d/dτ)[m_o]U + m_oA
F = dP/dτ = γdP/dt = γ(d/dt)[(E/c,p)] = γ(dE/cdt,dp/dt) = γ(Ė/c,ṗ) = γ(Ė/c,f)
gives the Power-Force acting on an SR particle at a particular event: SI Units [kg·m/s²].
( γ ) is the SR Lorentz gamma factor { γ = 1/√[1-β²]; β = u/c }, ( Ė = dE/dt ) is the power ( = temporal force) and ( f = ṗ = dp/dt ) is the spatial force.
The Lorentz Scalar Product F·F = γ(Ė/c,f)·γ(Ė/c,f) = γ²[(Ė/c)² - f·f]
Note:
F = dP/dτ
(F⁰,Fⁱ) = d(P⁰,Pⁱ)/dτ
(γĖ/c,γf) = d(E/c,p)/dτ
γ(Ė/c,f) = γd(E/c,p)/dt

The relativistic temporal component (F⁰) = d(P⁰)/dτ = d(E/c)/dτ = γd(E/c)/dt = γ(Ė/c)
The Newtonian temporal component (Ė/c) = d(E/c)/dt

The relativistic spatial component (Fⁱ) = d(Pⁱ)/dτ = γ(f) = d(p)/dτ = γd(p)/dt
The Newtonian spatial component (f) = d(p)/dt = (ṗ)

F = (d/dτ)[m_o]U + m_oA
F·U = (d/dτ)[m_o]U·U + m_oA·U = (d/dτ)[m_o]c² + m_o(0) = (d/dτ)[m_o]c²

If the force is applied to a particle of stable invariant rest mass m_o, (i.e. d/dτ[m_o] = 0 ↔ F·U = 0),
then the 4-Force is considered to be Pure (space-like), and can be written as:
4-ForcePure F_p = γ(u·f/c,f), with Ė = u·f
The Lorentz Scalar Product F_p·F_p = γ(u·f/c,f)·γ(u·f/c,f) = γ²[(u·f/c)² - f·f] = -(f_o·f_o) = -(f_o²)
An example of a pure force is the force due to an EM field:
4-Force_EM F_EM = γq( (u·e)/c, (e) + (u⨯b) ), the force on a charged particle due to an EM field.

If the force applied does not change the particle's 4-Velocity, ie. (A = 0),
then the force is considered to be Heat-like (time-like), and can be written as:
4-ForceHeat F_h = (d/dτ)[m_o]γ(c,u)= γ(d/dt)[m_o]γ(c,u) = γṁ(c,u) = γ²ṁ_o(c,u)
The Lorentz Scalar Product F_h·F_h = γṁ(c,u)·γṁ(c,u) = γ²ṁ²(c² - u·u) = ṁ²c² = (ṁc)² = (Ė/c)² = (γĖ_o/c)²
The action-reaction forces that occur in collisions are heat-like.
Another example of an impure force is one derived from a scalar potential:
4-ForceScalar F_s = k(∂_t[Φ],-∇[Φ]), which hasU·F_s = U·k ∂[Φ] = k(d/dτ)[Φ] = Ė = (d/dτ)[E_o]
=============================

4-ForceDensity F_den = γ(Ė_den/c,ṗ_den) = (ṁ_denc,ṗ_den)
F_den^μ = T^μν_,ν = ∂_νT^μν
gives the ForceDensity content of an SR particle/distribution at a particular event: SI Units [kg/m²·s²].
( γĖ_den ) is the energy_density rate of change ( = temporal force_density) of the event and ( γṗ_den ) is the spatial force_density.
The 4-ForceDensity (sometimes called the Lorentz Force Density) can be computed from a 4-Divergence of the Stress-Energy Tensor.
If the system is non-conservative, (eg. it interacts with other systems), then there will be a non-zero 4-ForceDensity.
We can also get an EM 4-ForceDensity:
Start with the regular EM 4-Force, and then divide by the invariant rest volume (V_o)
F_EM^μ = dP^μ/dτ = qU_ν(∂^μA_EM^ν - ∂^νA_EM^μ) = qU_νF^μν
F_EM^μ = qU_νF^μν
F_EM^μ/V_o = qU_νF^μν/V_o
F_denEM^μ = (q/V_o)U_νF^μν
F_denEM^μ = (ρ_o)U_νF^μν
F_denEM^μ = J_νF^μν
see Maxwell's eqns in curved SpaceTime
=============================

4-NumberFlux N = N_f = n(c,u) = (cn,nu) = (cn,n) = Σ_a[∫dτ δ⁽⁴⁾[X - X_a(τ)]dX_a/dτ]
N = N_f = n_oU = (N_tot/V_o)U
gives the Number density - Number flux content of an SR fluid: SI Units [#/m²·s].
( n ) is the number density [#/m³] and ( nu ) is the number flux [(#/m³)*(m/s)] = [#/m²·s].
The bit with the integral is the 4D version of the Dirac Delta function.
f[Y^μ] = ∫d⁴X^μ δ⁽⁴⁾[X^μ -Y^μ] f[X^μ], where the 4D Dirac Delta function is a Lorentz Invariant in Minkowski Space.
** Take care not to confuse with the 4-Null N**
The Lorentz Scalar Product N·N = (nc,nu)·(nc,nu) = (nc)² - (n)²u·u = (n_oc)²
gives the analogous NumberDensity-NumberFlux equation.
When the spatial part ( nu ) is 0, this gives a Lorentz invariant rest charge density n_o.
Relativistic number density n = γn_o
The total count of "items" (N_tot) in a given rest volume (V_o) is a Lorentz scalar invariant.
N_tot = n_oV_o = (γ/γ)n_oV_o = (γn_o)(V_o/γ) = (n)(V) = nV
The 4-NumberFlux N can be used in generating the Stress-Energy Tensor for SR Dust
T_dust^μν = P^μN^ν = m_oU^μn_oU^ν = m_on_oU^μU^ν = ρ_moU^μU^ν = ρ_moc²T^μT^ν = ρ_eoT^μT^ν = ρ_eoV^μ^ν
Effectively, any "particle-type" 4-Vector can be transformed into a "density-type" 4-Vector by multiplying by the rest number density n_o.
Likewise, any relativistic scalar n can be transformed into a "density-type" scalar by multiplying by the number density n.
Looking at the Hamiltonian (H) :Lagrangian (L) connection:
H + L = p·u
nH + nL = np·u
H + L = p·u = g·u
with Hamiltonian density H, Lagrangian density L, momentum density g
A flux is a <charge> density*velocity. SI Units [<charge>/m³] * [m/s] = [<charge>/m²·s].
A Flux 4-Vector is a Lorentz Scalar <charge> * 4-NumberFlux N., which is equal to a <charge-density> * 4-Velocity U.
<charge> * N = <charge> * n_o * U = <charge-density> * U
=============================

	Particle Count	Mass_Energy	(d/dτ)[Mass_Energy]	Entropy	EM Charge	WaveAngFreq	EM Potential
(Lorentz Scalar) <Potential>	Ω = -X·U (free worldline)	S_act= -X·P (free particle action)				Φ = -X·K (free wave phase)
-d/dτ[<Potential>] <Charge>*c²	U·U = c²	E_o = U·P = -U·∂[S] = -d/dτ[S] E_o = m_oc²				ω_o = U·K = -U·∂[Φ] = -d/dτ[Φ] ω_o = (ω_o/c²)c²
<Charge>	N (usually 1)	m_o = (E_o/c²)	(d/dτ)[m_o]	S_ent	q	(ω_o/c²)	(φ_o/c²)
Particle 4-Vector <Charge>U	U	P = -∂[S] P = m_oU = (E_o/c²)U	F = (d/dτ)[m_o]U + m_oA		J_q = qU	K = -∂[Φ] K = (ω_o/c²)U	A = (φ_o/c²)U
Density 4-Vector Flux 4-Vector <Charge>N <ChargeDensity>U	N = U_den = n_oU	G = P_den = n_oP G = u_moU = m_on_oU = m_oN G = U·T^μν/c²	F_d = F_den = n_oF F_d = -∂·T^μν	S = s_oU = S_entn_oU = S_entN	J = J_qden = n_oJ_q J = ρ_oU = qn_oU = qN	? = (ω_o/c²)N	? = (φ_o/c²)N
<ChargeDensity>	n_o	u_mo = (u_eo/c²) = n_om_o	(d/dτ)[u_mo]	s_o = n_oS_Ent	ρ_o = n_oq	n_o(ω_o/c²)	n_o(φ_o/c²)
4-Divergence = 0 Conservation Law	∂·N = 0 Conservation of Particle Count N	∂·G = 0 Conservation of Mass_Energy m_o	∂·F_d = 0 Conservation of Power??	∂·S = 0 Conservation of Entropy S_ent	∂·J = 0 Conservation of Charge q	∂·K = 0 Conservation of Wave_Freq?	∂·A = 0 Conservation of EM Potential (Lorenz Gauge)

SRQM 4-Vector : Four-Vector Motion of Lorentz Scalar Invariants, Conservation Laws & Continuity Equations

=============================

4-EntropyFlux S = s(c,u) = (cs,su) = (cs,s)
S = s_oU = S_entn_oU = S_entN = (k_Bln Ω)N
gives the EntropyDensity - EntropyFlux content of an SR fluid: SI Units [kg/K·s³].
( s ) is the entropy density [kg/K·m·s²] and ( su ) is the entropy flux [(kg/K·m·s²)*(m/s)] = [kg/K·s³].
** Take care not to confuse with the 4-UnitSpatial S**
The Lorentz Scalar Product S·S = (sc,su)·(sc,su) = (sc)² - (s)²u·u = (s_oc)²
gives the analogous EntropyDensity-EntropyFlux equation.
(also can think of this as EntropyDensity-EntropyDensityCurrent equation)
When the spatial part ( su ) is 0, this gives a Lorentz invariant rest entropy s_o.
Relativistic entropy density s = γs_o
Total Entropy (S_ent) is a Lorentz Scalar Invariant where entropydensity s = nS_ent and rest entropy density s_o = n_oS_ent
Entropy S_ent = ∫s d³x = k_B ln[Ω], where Ω = # of microstates for a given macrostate
Boltzmann's constant (k_B) is a Lorentz Invariant, and Ω is a counting operation, with is Lorentz Invariant.
For a Perfect Fluid, one gets the Conservation of 4-EntropyFlux (∂·S = 0), and hence, Conservation of Total Entropy S_ent
=============================

4-CurrentDensity J = ρ(c,u) = (cρ,ρu) = (cρ,j)
4-ChargeFlux J = ρ(c,u) = (cρ,ρu) = (cρ,j)
J = ρ_oU = qn_oU = qN
gives the charge-current density content of an SR particle, for example an electron: SI Units [C/m²·s].
( ρ ) is the charge density and ( j ) is the current density.
The Lorentz Scalar Product J·J = (ρc,j)·(ρc,j) = (ρc)² - j·j = (ρ_oc)²
gives the analogous ChargeDensity-CurrentDensity equation.
(also can think of this as ChargeDensity-ChargeFlux equation)
When the spatial part ( j ) is 0, this gives a Lorentz invariant rest charge density ρ_o.
Relativistic charge density ρ = γρ_o
Total Charge (q) is a Lorentz Scalar Invariant where charge density ρ = nq and rest charge density ρ_o = n_oq
Typically, this is the 4-EM_CurrentDensity, but could represent any kind of "charge", where the SI Units would be [<charge unit>/m²·s].
An example of its use:
(∂·∂)A_EM = μ_oJ : The Non-Homogeneous Maxwell EM Equation (if ∂·A_EM = 0 : Lorenz Gauge)
This can be used to derive classical EM.
The 4-CurrentDensity is often called the 4-Current (although technically that would have the wrong dimensional units)
The 4-Current would actually be V_o*4-CurrentDensity where V_o is the Lorentz scalar rest volume.
For a Perfect Fluid, one gets the Conservation of 4-CurrentDensity (∂·J = 0), and hence, Conservation of Total Charge (q).
Further, one can write:
(∂_μJ^μ[X^μ] = 0) and (∂_α∂^α)A_EM^ν[X^ν] = μ_oJ^ν[X^ν]): Both the 4-CurrentDensity and 4-VectorPotentials can be functions of the 4-Position.
=============================

4-VectorPotential A = (φ/c,a) = A[X] = A[(ct,x)] = (φ[(ct,x)]/c,a[(ct,x)])
A = (φ_o/c²)U {massive case}
A = (φ/c)N = (|a|)N {massless = photonic case, |a| is a "EM potential intensity" Lorentz scalar, N is a "unit" 4-Null}
A·U = 0 {A is Purely-Spatial case, as can happen with an EM wave}
A_EM = (φ_EMo/c²)U
A_{EMpointcharge} = (q/4πε_oc)U/[R·U]_ret = (qμ_oc/4π)U/[R·U]_ret {for a point charge q}
gives the potential-vector potential content of an SR potential/field which is spread out over SpaceTime, so technically A = A[X]: SI Units [kg·m/C·s].
( φ ) is the potential and ( a ) is the vector potential.
Sometimes known as: ( φ ) is the electric potential and ( a ) is the magnetic vector potential.
** Take care not to confuse with the 4-Acceleration A**
It is used as the relativistically correct way to specify fields that are "the gradient of a potential".
The most common form is the 4-EM-VectorPotential A_EM = (φ/c,a) = A_EM[X] = A_EM[(ct,x)] = (φ[(ct,x)]/c,a[(ct,x)]),
The Lorentz Scalar Product A·A = (φ/c,a)·(φ/c,a) = (φ/c)² - a·a = (φ_o/c)²
gives the analogous Potential-Vector Potential equation.
This is also known as the Dirac Gauge Condition, when A·A = constant.
When the spatial part ( a ) is 0, this gives a Lorentz invariant rest scalar potential φ_o.
Interesting limiting-cases are:
Rest Case: |u|→0, γ→1, |a|→0, then φ→φ_o {for rest/time-like} A = (φ/c,a)
Photonic Case: |u|→c, γ→∞, φ_o→0, then φ →|a|c; {for null/light-like} A = (|a|,a) = |a|(1,n̂)
(|p|)N = lim[P = m_oU; as m_o→ 0,|u|→ c]
If A·U = 0 = (φ_o/c²)U·U = (φ_o/c²)c² = φ_o, then φ_o = 0
If φ_o = 0, then A·U = (φ_o/c²)U·U = (φ_o/c²)c² = φ_o = 0
Thus, {A·U = 0} ↔ {φ_o = 0}
Relativistic scalar potential φ = γφ_o
Examples of its use:
(∂·∂)A_EM = μ_oJ : The Non-Homogeneous Maxwell EM Equation (if ∂·A_EM = 0 : Lorenz Gauge)
F^μ = dP^μ/dτ = qU_ν(∂^μA_EM^ν - ∂^νA_EM^μ) = qU_νF^μν : The Lorentz Force Equation, the force imposed on a test charge by an EM field
These can be used to derive classical EM.
=============================

4-PotentialMomentum Q = (U/c,q) = (qφ/c,qa)
Q = qA
gives the Potential Energy-Momentum content of the SR field it specifies: SI Units [kg·m/s].
( U ) is the potential energy ( = Potential temporal momentum) of the field, and ( q = qa ) is the Potential spatial momentum.
The Lorentz Scalar Product Q·Q = (U/c,q)·(U/c,q) = (U/c)² - q·q = (U_o/c)²
When the spatial part ( q = qa ) is 0, this gives a Lorentz invariant rest potential energy U_o.
Relativistic Potential Energy U = γU_o
P_T = P + Q = P + qA: The Total 4-Momentum is the sum of the Particle 4-Momentum + the external Field 4-Momentum
P = P_T - Q = P_T - qA: Same thing, but written as the Minimal-Coupling Rule
The main idea here is that the external fields which couple to a test particle contain both energy and momentum themselves.
Both particle and external field 4-Momenta must be accounted for so that the correct dynamics is obtained.
Typically this with be a charged particle (q) interacting with a 4-VectorPotential A, such as the EM field.
=============================

4-TotalMomentum P_T_particle = (E_T/c,p_T) = (H/c,p_T) = (E/c + U/c,p + q) = (E/c + qφ/c,p + qa), meaning the sum of particle momentum and charged interaction potential momentum
P_T = P + Q = P + qA
gives the Total Energy-Momentum content of an SR particle plus the SR field it is in: SI Units [kg·m/s = J].
( E_T = H ) is the Hamiltonian Total energy ( = Total temporal momentum) of the event and ( p_T ) is the Total spatial momentum.
The Lorentz Scalar Product P_T·P_T = (H/c,p_T)·(H/c,p_T) = (H/c)² - p_T·p_T = (H_o/c)²
When the spatial part ( p_T ) is 0, this gives a Lorentz invariant rest Hamiltonian H_o.
Relativistic Hamiltonian H = γH_o
The 4-TotalMomentum of a system can be split into the 4-Momentum of a Particle + a charge (q) times a 4-VectorPotential.
Essentially, we are examining a lone particle running around in a big field/potential which can affect the particle.
Both the particle and the field have 4-Momentum, and it is the sum of all 4-Momentuṁs that is conserved.
This is an alternate way of stating the Minimal-Coupling Rule, which can be written as P = P_T - qA.
Or perhaps the better way to say it is that the Minimal Coupling rule is a restatement of Conservation of 4-TotalMomentum.
The Total 4-Momentum of a system is the sum of all the 4-Momenta of its constituent parts.
This is used to derive the Classical EM laws.
The Conservation of 4-Momentum unites the Conservation of Energy and Conservation of 3-momentum into a single law,
and plays a major role in just about all physical effects.
The 4-TotalMomentum is often seen in the formulas using the Action S_act.
S_act = -∫(P_T·dR) = -∫(P_T·U)dτ = -∫(P_T·U/γ)dt = ∫L dt
S_act = -(P_T·R) and ∂[S_act] = -P_T.
Getting into Relativistic Analytic Mechanics, we can define an Action (S = S_act) as the negative Lorentz Scalar product of the 4-TotalMomentum with the 4-Position,
or the 4-TotalMomentum is the negative 4-Gradient of the Action.
An even more generalized version is:
P_Total = P_particle + P_potential + P_geometric
=============================

4-WaveVector
4-AngularWaveVector

K = (ω/c,k) = (ω/c,n̂ω/v_phase) = (ω/c,ωu/c²) = (ω/c)(1,β) = (1/cT,n̂/λ)

4-CyclicWaveVector K_cyc = (ν/c,k_cyc) = (ν/c,n̂ν/v_phase) = (ν/c,νu/c²) = (ν/c)(1,β) = (1/cT,n̂/λ)
K = (ω_o/c²)U {massive case}
K = (ω/c)N = (|k|)N {massless = photonic case, |k| is a "wavevector intensity" Lorentz scalar, N is a "unit" 4-Null}
K_cyc = (ν_o/c²)U
K = 2πK_cyc
K = dR/dθ = (K·∂)[R]
K = dX/dθ = (K·∂)[X]
gives the description of an SR wave, for example, a photon: SI Units [rad/m] for K, [cycles/m] for K_cyc.
( ω ) = 2πν is the temporal angular frequency and ( k ) = 2πk_cyc =2πn̂/λ is the spatial wave number, which is like an spatial angular frequency.
( ν ) is the temporal cyclic frequency and ( k_cyc ) = n̂/λ is the spatial cyclic wave number, which is like an spatial cyclic frequency.
It can also be described using:
( n̂ ) = the unit direction, ( v_phase ) = the wave (phase) velocity, ( u = v_group ) = the group velocity, ( β = u/c ) = the Relativistic Beta Factor,
( T ) = the period, ( λ ) = the wavelength,
( T ) = T/2π = reduced period, ( λ ) = λ/2π = reduced wavelength,
The Lorentz Scalar Product K·K = (ω/c,k)·(ω/c,k) = (ω/c)² - k·k = (ω_o/c)²
gives the analogous AngularFrequency-WaveVector equation.
When the spatial part ( k ) is 0, this gives a Lorentz invariant rest angular frequency ω_o.
Relativistic angular frequency ω = γω_o
v_phase = ω/k
v_group = dω/dk = u = event velocity for SR waves
from K·K: ω² = k²c² + ω_o²
ω²/k² = c² + ω_o²/k²
v_phase² = c² + ω_o²/k²
v_phase = √[c² + ω_o²/k²]
from K·K: ω² = k²c² + ω_o²
ω = √[k²c² + ω_o²]
v_group = dω/dk = (1/2)(1/√[k²c² + ω_o²])*2kc² = (1/ω)*kc² = kc²/ω = c²/v_phase = u = v_event
Hence, in SR, for massive or massless: v_group * v_phase = c²
Rindler gives a great way of understanding v_phase.
Imagine a rest frame with signal lamps at unit intervals along some line.
Set them so that you see them all flash simultaneously.
Now, Lorentz Boost (v_group) along the line.
The flashes will now appear to move along the row, like airport landing lamps.
The speed of the "moving" flash is v_phase.
So, in a sense, v_phase is the speed of simultaneity.

The 4-WaveVector K is used in the SR Doppler Equations, which give the Doppler red-shift, blue-shift, and transverse Doppler effects.
I need to emphasize here that the 4-WaveVector can exist as an entirely SR object (non-QM).
4-rays can be defined as those curves in SpaceTime which are everywhere in the direction of K.
They satisfy the equation { K = dX/dθ = (K·∂)[X] } for some parameter θ.
These curves are the orthogonal trajectories of the hypersurfaces representing the wavetrain.
===
For light rays, we have K·K → 0. {This applies only to massless particles/waves, they are 4-Null}
∂[K·K] = 2*K·∂[K] = ∂[0] = 0.
d² X/dθ² = dK/dθ = (K·∂)[K] = K·∂[K] = 0
So, these light rays are straight, in both 3D and 4D. See Rindler, Intro to SR, 2nd Ed., pg. 63.
===
The 4-WaveVector can be derived in terms of periodic motion, for which families of surfaces move through space as time increases,
or alternately, as families of hypersurfaces in SpaceTime, formed by all events passed by the wave surface.
The 4-WaveVector is everywhere in the direction of propagation of the wave surfaces.
More specifically, the 4-WaveVector K is orthogonal to a hypersurface of constant phase Φ {an ensemble of events E(t,x,y,z) that all share the same value of Φ}
i.e. K_μ = -∂Φ/∂X^μ, or in 4-Vector notation, after raising the index on both sides: K = - ∂[Φ] The 4-WaveVector is the negative 4-Gradient of the SR Phase.
The phase is chosen so that it decreases by unity as we pass from one wave crest to the next, in the direction of propagation of the waves.
The contravariant vector K^μ = dX^μ/dλ is a tangent vector to the particle trajectory.
From this structure, one obtains relativistic/wave optics, without ever mentioning QM.
An SR plane wave can be written in the form Ψ = Ae^i(K·X).
The nature of the amplitude (A) is not specified here. (A) could be a Lorentz Scalar=(0,0)-Tensor, a 4-Vector = (1,0)-Tensor, a 4-Tensor = (2,0)-Tensor, etc.
Notice an interesting comparison:
4-Position X = (ct,n̂x), with dimension of [length]
4-WaveVector K = (1/cT,n̂/λ), with dimension of [length^-1]
The 4-Position and 4-WaveVectors are inverses, which is why K·X = (ω/c,k)·(ct,x) = (ωt - k·x) = (t/T - n̂·x/λ) = -Φ_phase gives a dimensionless phase.
If K·U = 0 = (ω_o/c²)U·U = (ω_o/c²)c² = ω_o, then ω_o = 0
If ω_o = 0, then K·U = (ω_o/c²)U·U = (ω_o/c²)c² = ω_o = 0
Thus, {K·U = 0} ↔ {ω_o = 0}
see Special Relativity/Waves,
=============================

4-TotalMomentum P_T_sys = (E_T/c,p_T) = (H/c,p_T) = Σ_n[P_T_particle(n)], meaning that the total 4-Momentum of a system is the sum of all individual particle 4-Momenta in the system
4-TotalWaveVector K_T_sys = (ω_T/c,k_T) =(ω_T/c,k_T) = Σ_n[K_T_wave(n)], meaning that the total 4-WaveVector of a system is the sum of all the individual 4-WaveVectors in the system
P_T_sys = (E_T/c,p_T) = Σ_n[P_T_particle(n)]
K_Tsys = (ω_T/c,k_T) = Σ_n[K_T_wave(n)]
For both the 4-Momentum and the 4-WaveVector, individual 4-Vectors are additive and contribute to a Total 4-Vector for the system.
( E_T = H ) is the TotalEnergy or Hamiltonian of the System, and ( p_T ) the Total 3-vector Momentum of the System.
This carries forward into classical mechanics as well.
The total momentum of a system is the sum of all its individual parts.
Likewise for waves, the total resultant wave is the sum of all the individual waves.
=============================

4-WaveDifferential dK = (dω/c,dk)
dK = d[K]
gives the differential form of the 4-WaveVector: SI Units [rad/m].
( dω ) is the temporal wave differential and ( dk ) the spatial wave differential.
The Lorentz Scalar Product dK·dK = (dω/c)² - dk·dk = (dω/c)² - |dk|²
gives the invariant differential distance or interval or measure between infinitesimally close wave events.
When the spatial part ( dk ) is 0, this gives a Lorentz invariant rest time displacement dω_o.
Relativistic temporal displacement dω = γdω_o.
Basically, the rules of differential calculus still apply to Minkowski SpaceTime.
=============================

4-Gradient ∂ = ∂_X = (∂_t/c,-∇) = (∂_t/c,- del) → (∂_t/c, -∂_x, -∂_y,-∂_z) = (∂/c∂t,-∂/∂x,-∂/∂y,-∂/∂z)
4-PositionGradient ∂ = ∂_X = (∂_t/c,-∇) = (∂_t/c,- del) → (∂_t/c, -∂_x, -∂_y,-∂_z) = (∂/c∂t,-∂/∂x,-∂/∂y,-∂/∂z)
∂ = ∂^μ = η^μν ∂_ν = η^μν∂/∂X^ν = ∂/∂X_μ
is an SR functional that gives the structure of Minkowski SpaceTime: SI Units [1/m].
∂[X] = η^μν = ( )·( ) = The Scalar Product Dot and SpaceTime Projection Tensor.
( ∂_t ) is the partial wrt. time and ( ∇ = ∇_x ) is the gradient, the partial vector wrt. spatial dimensions (eg. {x,y,z} or {r,θ,z} or {r,θ,φ}, etc.).
Importantly, the 4-Gradient has the spatial component sign reversed from the other regular 4-Vectors.
It is commonly seen in tensor-notation, lower-index-form as ∂_μ = (∂_t/c,∇)
The Lorentz Scalar Product ∂·∂ = (∂_t/c,-∇)·(∂_t/c,-∇) = (∂_t/c)² - ∇·∇ = (∂_τ/c)²
gives the d'Alembertian equation (a wave equation), also known as the Lorentz Invariant d'Alembert operator.
When the spatial part ( ∇ = ∇_x ) is 0, this gives a Lorentz invariant rest partial ∂_to = ∂_τ., which would presumably be the partial as measured along a worldline.
Occasionally, one sees:
∂·∂ = (∂_t/c)² - ∇·∇
⎕ = (∂_t/c)² - ∆ , where ( ⎕ = ∂·∂ ) and ( ∆ = ∇·∇ ), but the notation is poor because sometimes people use ( ⎕² = ∂·∂ )
Technically, the 4-Gradient ∂ is derived from the partial operator of the 4-Position X = X^ν.
∂_ν = ∂/∂X^ν = (∂/c∂t,∂/∂x,∂/∂y,∂/∂z) and then it is index-raised to get the 4-Gradient ∂ = ∂^μ = η^μν∂_ν = (∂/c∂t,-∂/∂x,-∂/∂y,-∂/∂z)
That is why ∂ = ∂_X = (∂_t/c,-∇) has the negative sign in the spatial component, unlike the other standard physical SR 4-Vectors.
The d'Alembert operator (∂·∂) is the Laplace operator of Minkowski Space. Despite being a functional, the d'Alembertian is still a Lorentz Scalar Invariant.
The Green's function G[X - X'] for the d'Alembertian is defined as (∂·∂)G[X - X'] = δ⁽⁴⁾[X - X'], with { δ⁽⁴⁾ } as the 4-D Dirac Delta.
Gauss' Theorem in SR is { ∫_Ωd⁴X (∂·V) = ∮_∂ΩdS (V·N) },
where Ω is a 4D simply-connected region of Minkowski SpaceTime, ∂Ω = S is its 3D boundary with its own 3D Volume element dS and outward pointing normal N^μ.
The 4-Gradient is an extremely important SR 4-Vector which defines many properties and relations among the other SR 4-Vectors.
We will re-visit this 4-Vector operator again... it essentially is the connection between SR and QM.
=============================

4-WaveGradient ∂_K = (c∂_ω,-∇_k) = (c∂_ω,-del_k) → (c∂_ω, -∂_kx, -∂_ky,-∂_kz) = (c∂/∂ω,-∂/∂k_x,-∂/∂k_y,-∂/∂k_z)
∂_K = ∂_K^μ = η^μν ∂_Kν = η^μν∂/∂K^ν
is an SR functional that gives the structure of Minkowski SpaceTime: SI Units [m/rad].
( ∂_ω ) is the partial wrt. angular frequency and ( ∇_k ) is the wave-vector gradient, the partial vector wrt. the wave vector (eg. {k_x,k_y,k_z} or {k_r,k_θ,k_z} or {k_r,k_θ,k_φ}, etc.).
Technically, the 4-WaveGradient ∂_K is derived from the partial operator of the 4-WaveVector K = K^ν.
∂_Kν = ∂/∂K^ν = (c∂/∂ω,∂/∂k_x,∂/∂k_y,∂/∂k_z) and then it is index-raised to get the 4-WaveGradient ∂_K = ∂_K^μ = η^μν∂_K_ν = (c∂/∂ω,-∂/∂k_x,-∂/∂k_y,-∂/∂k_z)
That is why ∂_K = (c∂_ω,-∇_k) has the negative sign in the spatial component, unlike the other standard physical SR 4-Vectors.
The 4-WaveGradient is totally analogous to the 4-Gradient, or 4-PositionGradient, just replacing the 4-Position by the 4-WaveVector in the partial.
In other words, it's just math.
=============================

4-Polarization Ε = (ε⁰,ε) → (ε·β,ε) with (ε·β = 0)
is a *complex-valued* 4-Vector which can describe the polarization states of light rays: SI Units [1].
( ε⁰ ) is the temporal polarization and ( ε ) is the spatial polarization.
The Lorentz Scalar Product Ε·Ε = (ε⁰,ε)·(ε⁰,ε) = (ε⁰)² - ε·ε → -1. The 4-Polarization is normalized to have a magnitude of -1 (ie. it's spatial).
Since the 4-Polarization is orthogonal to the 4-WaveVector, (Ε·K = 0),
(ε⁰,ε)·(ω/c)(1,β) = (ω/c)(ε⁰*1 - ε·β) = 0, therefore (ε⁰ = ε·β),
one can write it as: 4-Polarization Ε = (ε·β,ε).
Normally this would give the 4-Polarization 3 independent components, but the spatial magnitude places an interesting restriction.
Since the 4-Polarization can have complex components, we make a slight modification:
Ε*·Ε = (ε·β,ε)*·(ε·β,ε) = (ε·β)* (ε·β) - ε*·ε = (ε·β)² - 1 = -1.
Therefore, (ε·β) = 0. Note that this condition can still be true with (ε) ≠ 0 and (β) ≠ 0. In this case the (ε) and (β) are simply orthogonal to each other.
For a massive particle, there is always a rest frame with (β = 0), so there is no further restriction and there are 3 independent polarizations.
For a massless particle, there is never a rest frame, (β = n̂), so (ε·n̂) = 0 is an additional restriction on the degrees of freedom,
which limits photonic particles/light-rays to 2 independent polarizations, both of which are orthogonal to direction of motion (n̂).
Note that both (Ε*·Ε = -1) and (Ε·K = 0) are Lorentz Invariant equations, and thus true for all observers.
More on this in the 4-UnitSpatial...
If we consider a 4-WaveVector → (ω/c,0,0,k_z,) with a spatial z-direction,
we get a 4-Polarization orthogonal to it:
→ (0,c_x,c_y,0)
→ (0,1,0,0) = x-polarized
→ (0,0,1,0) = y-polarized (rotated 90°)

for photon travelling in z-direction
using the Jones Vector formalism n = z / |z|
E = (0,1,0,0) : x-polarized linear
E = (0,0,1,0) : y-polarized linear
E = √[1/2] (0,1,1,0) : 45° from x-polarized linear
E = √[1/2] (0,1,i,0) : right-polarized circular
E = √[1/2] (0,1,-i,0) : left-polarized circular

General-polarized (elliptical)
E = (0,Cos[θ]Exp[iα_x],Sin[θ]Exp[iα_y]),0)
E* = (0,Cos[θ]Exp[-iα_x],Sin[θ]Exp[-iα_y]),0)

From Wikipedia: Photon Polarizaton:
"Much of the mathematical machinery of quantum mechanics, such as state vectors, probability amplitudes, unitary operators, and Hermitian operators, emerge naturally from the classical Maxwell's equations in the description.
The quantum polarization state vector for the photon, for instance, is identical with the Jones vector, usually used to describe the polarization of a classical wave.
Unitary operators emerge from the classical requirement of the conservation of energy of a classical wave propagating through lossless media that alter the polarization state of the wave.
Hermitian operators then follow for infinitesimal transformations of a classical polarization state."
=============================

4-Zero Z = (0,0) = 0^μ
is a special 4-Vector that is the same for all observers: SI Units [1].
Any Lorentz Transformation leaves the 4-Zero unchanged.
=============================

4-UnitTemporal T = γ(1,β)
T = U/c
gives the dimensionless measure in the temporal direction of an event in SpaceTime: SI Units [1].
( γ ) is the SR gamma factor { γ = 1/√[1-β²]; β = u/c }, ( 1 ) is the dimensionless temporal measure, and ( β ) is the dimensionless spatial measure, with {β → 0..1}.
The Lorentz Scalar Product T·T = γ(1,β)·γ(1,β) = γ²(1,β)·(1,β) = γ²(1² - β·β) = γ²(1 - β·β) = (1)
says that all SR events have invariant 4-UnitTemporal magnitude of 1 in the temporal direction, hence the name 4-UnitTemporal.
Note that this is true even in the limiting photonic case when |β| → 1.
When the spatial part ( β ) is 0, this gives a Lorentz invariant rest temporal measure 1.
In a rest frame,T → T_o = (1,0), and has 0 independent components.
4-UnitTemporal T = γ(1,β), and has 3 independent components, with 3 degrees of freedom from the motion β.
Generic 4-Vector A = (a⁰,a)
A·T = (a⁰,a)·γ(1,β) = γ(a⁰*1 - a·β) = γ(a⁰ - a·β) → (1)(a⁰_o - a·0) = a⁰_o
A·T = a⁰_o
The Lorentz Scalar product of any 4-Vector with the 4-UnitTemporal gives the Invariant Rest Value of the Temporal Component.
This makes sense from a vector viewpoint - you are taking the projection of the generic vector along a unit-length vector in the time direction.
The 4-UnitTemporal has only 3 independent components, given by the 3 degrees of freedom from the motion β.

Part of the reason for introducing this 4-Vector is to appease those physicists who insist on setting (c→dimensionless 1).
My own opinion is that setting (c→1) is a poor decision, as c is a fundamental constant with dimensional units of [velocity].
Instead, one can simply divide the 4-Velocity by (c) to get a dimensionless 4-Vector T = U/c,
which accomplishes much of the same math simplification without losing the value of dimensional analysis.

Also, it is the source of the:
Temporal "(V)ertical" Projection Tensor V^μν = T^μT^ν → Diag[1,0,0,0]
Spatial "(H)orizontal" Projection Tensor H^μν = η^μν - T^μT^ν → Diag[0,-1,-1,-1]
which together give:
SpaceTime Projection Tensor η^μν = V^μν + H^μν → Diag[1,-1,-1,-1]
=============================

4-UnitSpatial S = γ[β_n̂] (n̂·β,n̂) with (n̂ any direction) or S = (n̂·β,n̂) with (n̂·β = 0)
gives the dimensionless measure in a spatial direction of an event in SpaceTime: SI Units [1].
( γ ) is the SR gamma factor ( γ = 1/√[1-β²]; β = u/c ), ( n̂·β ) is the dimensionless temporal measure, and ( n̂ ) is the dimensionless spatial directional measure, with {β → 0..1}.
The Lorentz Scalar Product S·S = γ[β_n̂](n̂·β,n̂)·γ[β_n̂](n̂·β,n̂) = γ[β_n̂]²(n̂·β,n̂)·(n̂·β,n̂) = γ[β_n̂]²((n̂·β)² - n̂·n̂) = γ[β_n̂]²((n̂·β)² -1 ) = (-1)γ[β_n̂]²( 1 - (n̂·β)²) = (-1)
says that all SR events have invariant 4-UnitSpatial magnitude of 1 in the spatial direction, hence the name 4-UnitSpatial.
When the temporal motion part ( n̂·β ) is 0, this gives a Lorentz invariant rest spatial measure -1.
In a rest frame, S → S_o = (0,n̂), thus it has 2 independent components, with 2 degrees of freedom due to n̂.
4-UnitSpatial S = γ[β_n̂](n̂·β,n̂), and has 3 independent components, with 2 degrees of freedom from n̂, and 1 from the direction of motion β_n̂.
Why only 1 and not 3 from the β? Because the components of (β) orthogonal to (n̂) play no role in the 4-Vector.
Generic 4-Vector A = (a⁰,a)
A·S = (a⁰,a)·γ[β_n̂](n̂·β,n̂) = γ[β_n̂](a⁰* n̂·β - a·n̂) → (1)(a⁰*0 - a·n̂) = - a·n̂
A·S = - a·n̂
If we align S in the direction of A, then A·S_A = - a
The Lorentz Scalar product of any 4-Vector with the aligned 4-UnitSpatial gives the Invariant Rest Value of the Spatial Component.
This makes sense from a vector viewpoint - you are taking the projection of the generic vector along a unit-length vector in the same spatial direction.

This 4-Vector goes along with the 4-UnitTemporal, and is orthogonal to it.
T·S = γ(1,β)·γ[β_n̂](n̂·β,n̂) = γ[β]γ[β_n̂](1,β)·(n̂·β,n̂) = γ[β]γ[β_n̂](n̂·β - n̂·β) = 0

Let me back up for a moment: There are actually 2 classes of 4-UnitSpatial.
Consider the following:
Start with the 4-UnitTemporal as given: T = γ(1,β)
Let's construct the 4-UnitSpatial just based on the Lorentz Invariants.
Start with a generic 4-Vector S = (s⁰,s)
We want the 4-UnitSpatial to be orthogonal to the 4-UnitTemporal.
T·S = 0 = γ(1,β)·(s⁰,s) = γ(1*s⁰ - β·s), Hence s⁰ = β·s
S = (β·s,s)
We also want the 4-UnitSpatial Magnitude to be a negative number (-k), since space is the negative interval in our preferred convention.
S·S = -k = (β·s,s)·(β·s,s) = [(β·s)² - s·s]
We can write s = (s)n̂
S·S = -k = [(β·s)² - s·s] = (s)²[(β·n̂)² - n̂·n̂] = -(s)²[n̂·n̂ - (β·n̂)²] = -(s)²[1 - (β·n̂)²] = -k
Ok, here is where the choice comes in. By splitting s = (s)n̂, we have two ways to solve this.
======
(Class #1) Let s = ±√[k]γ[β_n̂] and n̂ = any direction
S·S = -(s)²[1 - (β·n̂)²] = -(±√[k]γ[β_n̂])²[1 - (β·n̂)²] = -(±√[k])²(γ[β_n̂])²[1 - (β·n̂)²] = -(±√[k])² = -(√[k])² = -k
S·S = -k
S = (β·s,s) with s = ±√[k]γ[β_n̂] and n̂ = any direction
For (k = 1) we get 4-UnitSpatial S = γ[β_n̂](n̂·β,n̂)
======
(Class #2) Let s = ±√[k] and n̂ = direction restricted by (β·n̂) = 0
S·S = -(s)²[1 - (β·n̂)²] = -(±√[k])²[1 - (0)] = -(±√[k])²[1] = -(±√[k])² = -(√[k])² = -k
S·S = -k
S = (β·s,s) with s = ±√[k] and n̂ = direction restricted by (β·n̂) = 0
For (k = 1) we get 4-UnitSpatial S = (n̂·β,n̂), with (n̂·β) = 0

This is actually an interesting exception to the 4-Vector Zero Component Lemma
S' = Λ S = γ'(1*(β·s) + β'·s, β'(β·s) + s) = γ'(β'·s,s) = (β'·s',s'), with s' = γ's
The Lorentz-boosted 4-Vector is in the same format, so we get 4-UnitSpatial S' = (s'·β',s'), with(s'·β') = 0,
which is as it should be since S·S = -1 is a Lorentz Invariant equation.
Even though the temporal component is always 0, the overall 4-Vector is not the 4-Zero.
The exception is due to the scalar product. There are 3 ways it can equal 0 = (a·b) = |a||b|cos[θ].
The Lemma holds if either |a| = 0 or |b| = 0. The exception occurs when (a) is orthogonal to (b), when (θ = π/2), ie. when cos[θ] = 0 = (a·b).

Now, to another interesting side effect:
4-UnitSpatial S = (s·β,s), with (s·β) = 0
For a massive particle, there is always a rest frame with (β = 0), so (s) has 3 degrees of freedom.
For a massless particle, there is never a rest frame, (β = n̂), so (s) has only 2 degrees of freedom due to extra restriction (s·n̂) = 0,
with the spatial component (s) orthogonal to the direction of motion (n̂).
This exactly how the 4-Polarization works: 4-Polarization Ε = (ε⁰,ε) → (ε·β,ε) with (ε·β = 0)
======
For { k = 1} we get 4-Polarization Ε = (ε·β,ε), with (ε·β) = 0
For { k = (E_o/c)²} we get (E_o/c)S = (E_o/c)(β·s,s) = ((E_o/c)β·s,(E_o/c)s) = (p·s,(E_o/c)s) → The 4-Pauli-Lubanski-Vector W
Remember that these were generated by T·S = 0 = U·S = 0.
======
Hmm.... now does this mean there are 2 classes for the 4-UnitTemporal?
Start with the 4-UnitSpatial as given: S = γ[β_n̂](n̂·β,n̂)
Let's construct the 4-UnitTemporal just based on the Lorentz Invariants.
Start with a generic 4-Vector T = (t⁰,t)
We want the 4-UnitTemporal to be orthogonal to the 4-UnitSpatial.
S·T = 0 = γ[β_n̂](n̂·β,n̂)·(t⁰,t) = γ[β_n̂]((n̂·β)*t⁰ - n̂·t), Hence t = t⁰ β for any direction n̂.
T = (t⁰,t⁰ β) = t⁰(1,β), and we still have 4 independent components.
We also want the 4-UnitTemporal Magnitude to be a positive number (k), since time is the positive interval in our preferred convention.
T·T = k = t⁰(1,β)·t⁰(1,β) = (t⁰)²[(1)² - β·β] = k
There is really only one choice.
Choose t⁰ = ±√[k]γ[β], then T = ±√[k]γ[β](1,β), and with k = 1 we get T = γ[β](1,β) = γ(1,β), with 3 degrees of freedom, which is what we expect.
If we had chosen t⁰ = ±√[k] with the condition (β·β = 0), then you end up with the static 4-Vector (1,0), which has no degrees of freedom.

Fermi-Walker Transport and Thomas Precession of the 4-UnitSpatial
T·S = 0
Since U·S = 0
then d/dτ[U·S] = 0 = d/dτ[U]·S + U·d/dτ[S] = A·S + U·d/dτ[S]
U·d/dτ[S] = - A·S
if we assume d/dτ[S] = (k)*U then
U·d/dτ[S] = kU·U = kc² = -A·S
k = -A·S/c²
then d/dτ[S] = (-A·S/c²)U = (-A·S/c)T ,
which is Fermi-Walker Transport of the 4-UnitSpatial, and leads to Thomas Precession.
Fermi-Walker Transport is the way of transporting a purely spatial vector along the worldline of the particle in such a way that it is as "rotationless" as possible,
given that it must remain orthogonal to the worldline.
This choice also implies that d/dτ[S·S] = 0, since d/dτ[S·S] ~ [U·S] = 0,
which means that the magnitude of the 4-UnitSpatial is constant .

=============================

4-"Unit"Null N = (1,n̂) {dimensionless}
4-Null N = I_n(1,n̂) {takes on the dimension of I_n)
N = lim_{( |β|⟶1 )}[T = γ(1,β)] = lim_{( |β|⟶1 )}[S = γ(n̂·β,n̂)]
is the limit of either the 4-UnitTemporal or the aligned 4-UnitSpatial as ( β→1, γ→Infinity ):
SI Units [1] for the "Unit"Null, SI Units [I_n] for a physical 4-Null.
It represents photonic/light-like 4-Vectors.
The factor of ( I_n ) is a Lorentz Scalar "null-intensity" or "null-magnitude" and is somewhat arbitrary.
It can take any value (other than 0) and still represent the same photonic.
( I_n ) will be "set" depending on the actual relation of a 4-Vector to the 4-Null. {eg. P = |p|N, K = |k|N}
i.e. a photon has a frequency that depends on the motion of the observer, even though it is the same photon.
If the ( I_n ) = 0, then 4-Null N becomes 4-Zero Z.
( n̂ ) is the direction of motion.
This is due to fact that a Lorentz-Boosted photon is still the same photon, but with an altered value of ( I_n ) and ( n̂ ).
** Take care not to confuse with the 4-NumberFlux N**
The Lorentz Scalar Product N·N = I_n(1,n̂)·I_n(1,n̂) = I_n²(1,n̂)·(1,n̂) = I_n²(1² - n̂·n̂) = I_n²(1 - 1) = (0)
says that all SR null events have invariant 4-Null magnitude of 0, hence the name Null.
The 4-Null has only 3 degrees of freedom, 1 from the ( I_n ), and 2 from the direction of motion ( n̂ ).
So, a length and direction, but no dimensional units.
Therefore, one can build up other photonic 4-Vectors by multiplying by a Lorentz scalar, giving a total of 4 degrees of freedom.
It is the source of the Null Projection Tensor N^μν = N^μN^ν = V^μν - (1/3)H^μν → Diag[1,1/3,1/3,1/3]
=============================

4-UnitHyperSurfaceNormal N = (n⁰,n) with ( N·N ) = {1 for time-like, 0 for light-like, -1 for space-like}
is the normalized 4-Vector pointing outward from a 4D HyperSurface at each point: SI Units [1].
A HyperSurface in an n-dimensional space is a surface of dimension (n-1).
Hence, for Minkowski Space (dim = 4), the HyperSurface is a "boundary/surface" of (dim = 3), technically a volume in this case.
The 4-UnitHyperSurfaceNormal is used in the 4D Gauss/Divergence Theorem.
=============================

All of the "basic" directional mathematical vectors, {(T)emporal, (S)patial, (N)ull} have 3 degrees of freedom,
which allows new physical 4-Vectors (with 4 dof.) to be created by multiplying by a Lorentz Scalar.

Let me emphasize that all these 4-Vectors are purely from SR - no Quantum Axioms are required.

Standard Physical SR 4-Vector Relations (Physical Laws)

I will introduce the SR Physical 4-Vectors, which encapsulate the Physical Properties of Nature.
I will show how these SR 4-Vectors are related to one another in purely relativistic theory, i.e. the Physical Laws of Nature.
These SR 4-Vectors can be linked to one another by Lorentz Scalar Invariants.
These Invariants are fundamental constants which can be empirically measured by physical experiment.

As already noted, time and space are linked via the Lorentz Scalar c = √[U·U] = U·T.
The invariant constant (c, the speed of light) may be measured using a light pulse generator/receiver, a mirror, a meter-stick, and a timer.
--A| c→ |B
*A| ←c |B
Set the light source/receiver at A, the mirror at B.
Measure the distance AB with the meter-stick.
Fire a light pulse from (A) to the mirror (B) while starting the timer.
Stop the timer when the returning pulse is detected back at (A).
c = Distance[A→B→A]/Time[A→B→A].

Note that this factor (c) appears in just about all Physical SR 4-Vectors, as it links the temporal components to the spatial components,
giving each component the correct physical dimensional units, ie. the overall 4-Vector has the same physical units as the 3-vector component in this notation.

R = (ct,r)
U = γ(c,u)
A = γ(cγ̇,γ̇u + γa)
P = (E/c,p) = (mc,p)
F = γ(Ė/c,f) = γ(ṁc,f)
N = n(c,u)
S = s(c,u)
J =ρ(c,u) = (cρ,j)
A = (φ/c,a)
Q = (U/c,q)
P_T = (H/c,p_T)
K = (ω/c,k) = (1/cT,n̂/λ)
∂ = (∂_t/c,-∇)
For some of the dimensionless 4-Vectors, the factor of (c) is hidden in the Beta factor (β = u/c) so that the overall 4-Vector is dimensionless.
Ε = (ε⁰,ε) → (ε·β,ε), with (ε·β = 0)
T = γ(1,β)
S = γ[β_n̂] (n̂·β,n̂) with (n̂ any direction) or S = (n̂·β,n̂) with (n̂·β = 0)

The only exception I can think of is the 4-Null
N = I_n(1,n̂)
This is because time and space are completely blended for the Null-Case ( |u|→ c, and therefore β → cn̂/c) so the c's cancel out.
However, even in this case, let's look at the 4-Momentum P = (E/c,p) → (|p|,p). We still get E = |p|c for photons.
========================================================

So, to reiterate, the invariant scalar products of individual 4-Vectors...
R·R = (cτ)² or (0) or -(r_o²), depending on the actual event interval
U·U = (c)²
A·A = -(a_o²)
dR·dR = (cdτ)² or (0) or -(dr_o²), depending on the actual event interval
ΔR·ΔR = (cΔτ)² or (0) or -(Δr_o²), depending on the actual event interval
P·P = (m_oc)² = (E_o/c)²
F·F = γ²[(Ė/c)² - f·f]
F_p·F_p = -(f_o²)
F_h·F_h = (γĖ_o/c)²
N·N = (n_oc)²
S·S= (s_oc)²J·J = (ρ_oc)²
A·A = (φ_o/c)² or [(φ/c)² - a·a]
Q·Q = (U_o/c)²
P_T·P_T = (H_o/c)²
K·K = (ω_o/c)² = (1/cT_o)²
∂·∂ = (∂_τ/c)²

T·T = (1) Unit Temporal
T·S = (0) They are orthogonal
S·S = (-1) Unit Spatial
N·N = (0) Null 4-Vector is orthogonal to itself
========================================================

Scalar Products and other SR 4-Vector Relations (Physical Laws)

I will introduce the SR Physical 4-Vectors, which encapsulate the Physical Properties of Nature.
I will show how these SR 4-Vectors are related to one another in purely relativistic theory, i.e. the Physical Laws of Nature.
Now consider the links between different 4-Vectors.
Some of these are simply mathematical consequences of the 4-Vector definitions, others are found by empirical experiment.
*Note* Everything in green are relativistically correct covariant equations, which are valid for all observers.
Use of the Lorentz Scalar Product provides many fundamental relations. see List of Relativistic Equations,...
========================================================

∂ = ∂^μ = η^μν∂_ν = η^μν∂/∂X^ν
The 4-Gradient is the index-raised partial wrt. the 4-Position.
It is one of the most fundmental of the 4-Vectors, as it relates things in both classical SR and QM.
∂ = ∂^μ = η^μσ∂_σ = η^μσ∂/∂X^σ
∂^μX^ν = η^μσ∂_σX^ν = η^μσ(∂/∂X^σ)X^ν = η^μσ(∂X^ν/∂X^σ) = η^μσ(δ_σ^ν) = η^μν
=============================

∂·X = 4
Tr[η^μν] = Tr[∂^μX^ν] = η_μνη^μν = η_μ^μ = δ_μ^μ = 4
The divergence or dimensionality of SpaceTime is 4 (i.e., that's why they are called 4-Vectors).
∂·X = (∂_t/c,-∇)·(ct,x) = (∂_t/c[ct] - (-∇·x)) = (∂_t[t] + (∇·x)) = (∂_t[t]) + (∂_x[x] + ∂_y[y] + ∂_z[z]) = (1) + (3) = 4
η_μνη^μν = η_μ^μ = η_ν^ν = δ_μ^μ = 1+1+1+1 = 4
Btw, an interesting proof for the 4D-ness of our universe (1 time + 3 space) is the first few rows of the Periodic Table of Elements.
There are 2 elements in the 1st row, a spin-up and a spin-down, where the electron s-orbitals are spherical (totally spatially symmetric).
There are 2 + 6 = 8 elements in each the 2nd and 3rd row. Again the 2 in s-orbitals. But then there are the spin-up and spin-down for 3 p-orbitals.
The p-orbitals are double-lobe-shaped, with the 3 double-lobes centered on the origin and aligned along 3 orthogonal spatial axes,
for a total of 6 evenly-spaced lobes (+x,-x,+y,-y,+z,-z).

Atomic #	1	2
Element	H	He
Electron Config	1s¹	1s²
Orbital Added	1s_t↑ ~ +t	1s_t↓ ~ -t

Atomic #	3	4	5	6	7	8	9	10
Element	Li	Be	B	C	N	O	F	Ne
Electron Config	[He]2s¹	[He]2s²	[He]2s²2p¹	[He]2s²2p²	[He]2s²2p³	[He]2s²2p⁴	[He]2s²2p⁵	[He]2s²2p⁶
Orbital Added	2s_t↑ ~ +t	2s_t↓ ~ -t	2p_x↑ ~ +x	2p_x↓ ~ -x	2p_y↑ ~ +y	2p_y↓ ~ -y	2p_z↑ ~ +z	2p_z↓ ~ -z
	Alkali Metals Group 1 S-Block	Alkaline Earth Metals Group 2 S-Block	Icosagens Group 13 P-Block	Crystallogens Group 14 P-Block	Pnictogens Group 15 P-Block	Chaocogens Group 16 P-Block	Halogens Group 17 P-Block	Aerogens - Noble Gases Group 18 P-Block
Atomic #	11	12	13	14	15	16	17	18
Element	Na	Mg	Al	Si	P	S	Cl	Ar
Electron Config	[Ne]3s¹	[Ne]3s²	[Ne]3s²3p¹	[Ne]3s²3p²	[Ne]3s²3p³	[Ne]3s²3p⁴	[Ne]3s²3p⁵	[Ne]3s²3p⁶
Orbital Added	3s_t↑ ~ +t	3s_t↓ ~ -t	3p_x↑ ~ +x	3p_x↓ ~ -x	3p_y↑ ~ +y	3p_y↓ ~ -y	3p_z↑ ~ +z	3p_z↓ ~ -z

If there were more dimensions, then there ought to be more than the 3 orthogonal lobes (x,y,z).
Neon [Ne] would be spaced differently from Argon [Ar]...
Spectroscopy shows that there are the same elements throughout the universe... so it has the same dimensions everywhere...
A similar argument can be made for the equation of state of a photon gas.
The energy density is 3*the pressure, where that 3 comes from dimensional arguments.
Just another note, this is another good reason to use the (t0+ℝ) Metric signature which gives 4-Vector (ct,x,y,z).
See also: Privileged character of 3+1 SpaceTime.
=============================

d/dτ(∂·X) = d/dτ(4) = 0
leads to
(∂·U) = 0
d/dτ(∂·X) = d/dτ(∂)·X = ∂·d/dτ(X) = 0
d/dτ(∂·X) = d/dτ(∂)·X = ∂·U = 0
∂·U = -d/dτ(∂)·X
∂·U = -(U·∂)[∂]·X
∂·U = -(U_ν∂^ν)[∂_μ]X^μ
∂·U = -U_ν∂^ν∂_μXμ
From here, two different routes
∂·U = -U_ν∂^ν∂_μX^μ
∂·U = -U_ν∂_μ∂^νX^μ
∂·U = -U_ν∂_μη^ν^μ
∂·U = -U_ν0^ν
∂·U = -0 = 0
Or
∂·U = -U_ν∂^ν∂_μX^μ
∂·U = -U_ν∂^ν(∂_μX^μ)
∂·U = -U_ν∂^ν(4)
∂·U = -U_ν0^ν
∂·U = -0 = 0
The ProperTime Derivative of {∂·X = 4} Relation gives Conservation of 4-Velocity.
This could be Conservation of a particle 4-Velocity, or Conservation of a 4-Velocity flow-field.
This leads to the Conservation Laws of various other 4-Vectors, since:
∂·(Lorentz Scalar Constant)U = 0
∂·(Interesting 4-Vector) = 0
Since the 4-Velocity has only 3 independent components, multiplying by a Lorentz Scalar (1 independent component), gives a 4-Vector with 4 independent components.
This relation is the foundation of the Conservation Laws for any 4-Vector formed in this manner.
∂·(Lorentz Scalar Constant)U = (∂_t/c,-∇)·(Lorentz Scalar Constant)γ(c,u) = ∂_t[γ(Lorentz Scalar Constant)] + ∇·γ(Lorentz Scalar Constant)u = 0
∂·(Interesting 4-Vector) = 0 is a local continuity equation, which says:
the change in time of γ(Lorentz Scalar Constant) at any local point is balanced by the flow of γ(Lorentz Scalar Constant)u into or out-of that point.
So, primary example is Conservation of Charge
∂·(Lorentz Scalar Constant ρ_o)U = ∂·(ρ_o)U = ∂·J = ∂_t[γ(ρ_o)] + ∇·γ(ρ_o)u = ∂_t[ρ] + ∇·ρu = ∂_t[ρ] + ∇·j = 0
∂_t[ρ] = -∇·j : The change in time of relativisitic charge density (ρ) at any local point is balanced by the flow of charge flux (j) into or out-of that point.
SRQM 4-Vector : Four-Vector Motion of Lorentz Scalar Invariants, Conservation Laws & Continuity Equations

=============================

∂[X] = η^μν = ( )·( ) = The Scalar Product Dot and SpaceTime Projection Tensor
The Minkowski Metric, a rank-2 tensor, which is at the heart of all SR, can be built of the more basic 4-Gradient and 4-Position.
The 4-Gradient acting on a 4-Vector gives a 4-Tensor.
∂[X] = ∂^μ[X^ν] = (∂_t/c,-∇)[(ct,x)] =

[(∂_t/c)ct,(∂_t/c)x,(∂_t/c)y,(∂_t/c)z]
[-∂_xct, -∂_xx, - ∂_xy, -∂_xz]
[-∂_yct, -∂_yx, -∂_yy, -∂_yz]
[-∂_zct, - ∂_zx, -∂_zy, -∂_zz ] =

[∂_tt, 0 , 0, 0 ]
[0 ,-∂_xx, 0, 0 ]
[0 , 0 ,-∂_yy, 0 ]
[0 , 0 , 0,-∂_zz ] =

[[∂_t/[t], -∇[x]]] =

[1, 0, 0, 0]
[0,-1, 0, 0]
[0, 0,-1, 0]
[0, 0, 0,-1] =

= Diag[+1,-1] = η^μν

The 4-Gradient of the 4-Position gives the Minkowski Metric η^μν.
This is a standard use of the Jacobian Matrix, which is all the component partial derivatives of a vector-valued function.
A shorter way of showing this is: ∂^μX^ν = η^μσ∂_σX^ν = η^μσ(∂/∂X^σ)X^ν = η^μσ(∂X^ν/∂X^σ) = η^μσ(δ_σ^ν) = η^μν.
The Minkowski Metric η^μνessentially is the "dot ( )·( )" of the Lorentz Invariant Scalar Product Relation.
A'·B' = A^μ'η_μ'ν'B^ν' = (Λ^μ'_αA^α) η_μ'ν'(Λ^ν'_βB^β) = (Λ^μ'_αη_μ'ν'Λ^ν'_β) A^αB^β = (Λ_ν'αΛ^ν'_β) A^αB^β = (η_αρΛ^ρ_ν'Λ^ν'_β) A^αB^β = (η_αρδ^ρ_β) A^αB^β = (η_αβ) A^αB^β = A^α(η_αβ)B^β = A·B
We will also see this used in the Invariant Trace of 2-index tensors,
Minkowski Metric Tensor η^μν = ∂^μ[X^ν] = Diag[+1,-1,-1,-1] = Diag[+1,-I] = Scalar Product ( _μ)·( _ν) {for (0,1)-Tensors}
Trace[ ^μν] = Tr[ ^μν] = η_μν = Diag[+1,-1,-1,-1] = Scalar Product ( ^μ)·( ^ν) {for (1,0)-Tensors}
The Trace: Tr[T^μν] = η_μνT^μν = T_ν^ν = T^μ_μ
A·B = A^μη_μνB^ν = A_νB^ν = A^μB_μ = + a⁰b⁰ -a¹b¹ -a²b² -a³b³ = + a⁰b⁰ -a·b = Lorentz Scalar
Tr[C^μν] = η_μνC^μν = + c⁰⁰ - c¹¹ - c²² - c³³ + (all other elements zero) = Lorentz Scalar
Notice that the Trace in SR is modified from being just a pure sum of the diagonal elements.
In fact, you can even regard the Trace and the Scalar Product as the exact same operation.
Consider that C^μν is an exterior product of the 4-Vectors: C^μν = A^μ x B^ν = A^μB^ν
Then the Trace operator (η_μν) is the scalar product rule: Tr[C^μν] = η_μνC^μν = η_μνA^μB^ν = A^μη_μνB^ν = A·B = Lorentz Scalar
However, there may be cases when the C^μν can't be split this way...
=============================

∂[X·X] = ∂[(cτ)²] = 2X
∂[X·X] = ∂[(cτ)²] = 2X·∂[X] = 2X^αη_ανη^μν = 2X^αη_α^μ = 2X^μ = 2X
The 4-Gradient acting on a Scalar gives another 4-Vector.
Since X·X = (cτ)² = (ct)² - x·x , this give the interesting relation:
X = (1/2)∂[(cτ)²] = c²τ∂[τ] = (1/2)∂[(ct)² - x·x] = (1/2)*{∂[(ct)²- x·x]/∂ct, -∇[(ct)²- x·x])} = (1/2)*{(c)²∂[(t)²]/∂ct, -∇[- x·x])} = (1/2)*{(2ct,2x)} = (ct,x) = X
=============================

X = (c²τ)∂[τ] = (X·U)∂[τ] = {(X·U)/(U·U)}U
This is a vector projection of X along U
=============================

∂[τ] = ∂[X·U/c²] = U/c² = U/(U·U)
An interesting relation, which can find some use in the Hamilton-Jacobi relation and the relativistic Action
=============================

∂·∂[X] = ∂_μη^μν = 0^ν = (0,0) = Z
The d'Alembertian of the 4-Position = the 4-Divergence of the Minkowski Metric = 4-Zero.
∂·∂[X] = (∂_t/c,-∇)·(∂_t/c,-∇)[(ct,x)] = ( (∂_t/c)² - ∇·∇)[(ct,x)] = ( ( (∂_t/c)² - ∇·∇)[ct],( (∂_t/c)² - ∇·∇)[x] ) = ( (∂_t/c)²[ct], - ∇·∇)[x] ) = (0,0) = Z
Basically, you are going from X to a constant with the 1st derivative, and then from a constant to zero with the 2nd deriviative.
This also shows that the 4-Divergence of the Minkowski Metric is the 4-Zero.
∂[X] = ∂^μ[X^ν] = η^μν
(∂·∂)[X] = ∂·∂[X] = ∂·[η^μν] = ∂_μ[η^μν] = 0^ν
=============================

∂·∂[X·X] = ∂·∂[(cτ)²] = 8
∂·∂[X·X] = ∂·[∂[X·X]] = ∂·[2X] = 2∂·[X] = 2(4) = 8
More practice with the 4-Gradient as the d'Alembertian.
=============================

U·∂ = d/dτ = γ(d/dt)
T·∂ = d/cdτ = γ(d/cdt)
The Scalar Product of the 4-Velocity with the 4-Gradient gives the Derivative wrt. Proper Time.
U·∂ = γ(c,u)·(∂_t/c,-∇) = γ(∂_t + u·∇) = γ(d/dt) = d/dτ
d/dτ = (dX/dX)(d/dτ) = (dX/dτ)(d/dX) = U^μ∂_μ = U·∂
This is a purely mathematical consequence of the definition of 4-Velocity and 4-Gradient.
The function (d/dτ) is a Lorentz Scalar.
see the "Invariant Rest Value of the Temporal Component Rule".
Event Tracking Relations

		Event R	Mass m_o = ρ_moV_o Energy E_o = m_oc²	MassDensity ρ_mo = n_om_o EnergyDensity u_eo = ρ_moc²
Derivative of 4-Position	dⁿR/dτⁿ	Event 4-Vector	particle	density
0th	R d⁰R/dτ⁰	pos: R = (ct,r)	m_o at R	ρ_mo at R
1st	dR/dτ d¹R/dτ¹	vel:U = dR/dτ	P = m_odR/dτ P = m_oU = (E_o/c²)U	G = ρ_modR/dτ G = ρ_moU = (u_eo/c²)U
2nd	d²R/dτ²	accel: A = dU/dτ	F = dP/dτ	F_d = dG/dτ
3rd	d³R/dτ³	jerk: J = dA/dτ jolt, surge, lurch: alt names
4th	d⁴R/dτ⁴	snap: S = dJ/dτ jounce: alt name
5th	d⁵R/dτ⁵	crackle: C = dS/dτ
6th	d⁶R/dτ⁶	pop: P = dC/dτ

In full GR, one must go to the fully covariant derivative.
D/Dτ = U^μ∇_μ = U^μ∂_μ + Γ^ν_μλU^μ
where the _λ-index acts on the 4-Vector argument (J^λ) and Γ^ν_μλU is a Christoffel Symbol.
Thus: D(J^λ)/Dτ = U^μ∇_μ(J^λ) = U^μ∂_μ(J^λ)+ Γ^ν_μλU^μ(J^λ)
There are alternate versions depening on the form of the argument, a type (m,n)-tensor.

=============================

τ = √[R·R/U·U] = √[(cτ)²/(c)²] = √[τ²] = τ
τ = (R·U/U·U) = (c²τ)/(c)² = τ
Δτ = (ΔR·U/U·U)
dτ = (dR·U/U·U)
The Proper Time (τ) is a Lorentz Scalar.
(Δτ) is the Invariant Interval between events connected by a worldline that is at rest,
i.e. the temporal distance between event A and event A', for which the event A doesn't move spatially but temporally evolves into event A'.
A' ----
| |
| (Δτ)
| |
A ----
If we continue the vector projection formula, we get:
τ = (R·U/U·U)
τU = (R·U/U·U)U = τγ(c,u) = γτ(c,u) = γt_o(c,u) = t(c,u) = (ct,ut) = (ct,r) = R
R = τU for R along U
=============================

∂[τ] = ∂[R·U/c²] = U/c² = U/(U·U)
An interesting relation, which can find some use in the Hamilton-Jacobi relation and the relativistic Action
=============================

U·ΔX = c²Δτ
T·ΔX = cΔτ
The 4-Vector way to define Simultaneity.
This is a relation that can used to determine whether events (at X₁ and X₂) are simultaneous in a given reference frame U.
Simultaneity is relative to the motions of the observers, and was one of the thought-experiments that led Einstein to the rules of SR.
U·ΔX = γ(c,u)·(cΔt,Δx) = γ(c²Δt -u·Δx) = c²Δt_o = c²Δτ
If Lorentz Scalar (U·ΔX = 0 = c²Δτ ), then the Proper Time displacement is zero,
and the event separation (ΔX = X₂ - X₁) is orthogonal to the worldline U.
X₁ and X₂ are therefore simultaneous for the observer on this worldline U.
Examining the equation we get γ(c²Δt -u·Δx) = 0.
The time difference between the events is (Δt = u·Δx/c²)
The condition for simultaneity in an alternate frame (moving at 3-velocity u wrt. the worldline U) is Δt = 0, which implies (u·Δx) = 0.
This can be met by:
(|u| = 0 ), the alternate observer is not moving wrt. the events, i.e. is on U or on a worldline parallel to U.
(|Δx| = 0 ), the events are at the same spatial location (co-local).
(u·Δx = 0 ), the alternate observer's motion is perpendicular (orthogonal) to the spatial separation Δx of the events in that frame.
If none of these conditions is met, then the events will not be simultaneous in the alternate reference frame.
Another case, for orthogonality, but not strict simultaneity, is (c²Δt = u·Δx)
If (|u| = c ), the worldline for a photon, then |Δx/Δt| = c, the events must be separated by light paths.
============
Note that we can get the a similar result by taking the Lorentz Transform of the displacement 4-Vector:
ΔX = (cΔt,Δx)
ΔX' = (cΔt',Δx') = ΔX^β' = Λ^β'_αΔX^α = γ[[1 - β],[- β1]](cΔt,Δx) = γ([1*cΔt - β·Δx],[- β*cΔt + 1* Δx]) = γ(cΔt - β·Δx, - β*cΔt + Δx])
Taking the temporal component:
cΔt' = γ(cΔt - β·Δx)
c²Δt' = γ(c²Δt -u·Δx) = Temporal Component of c*ΔX'
Compare with:
c²Δτ = γ(c²Δt -u·Δx) = U·ΔX
see the "Invariant Rest Value of the Temporal Component Rule"
=============================

dR = Udτ
A handy calculus trick that can be used in the Action/Lagrangian formulations
dR = dR(dτ/dτ) = (dR/dτ)dτ = Udτ
S_act = -∫(P_T·dR) = -∫(P_T·U)dτ = -∫(P_T·U/γ) dt = ∫L dt
This also shows that the combination (L dt) is a Lorentz Scalar, although separately (L) and (dt) are not.
R = τU for R along U
dR = d[τU] = d[τ]U + τd[U] = d[τ]U + (0) = Udτ, assuming d[U] is the 4-Zero Z (ie. not accelerating).
=============================

U = dR/dτ = (U·∂)[R]
T = dR/cdτ = (T·∂)[R]
4-Velocity is the derivative of 4-Position wrt. Proper Time τ.
U = dR/dτ = γdR/dt = γ(d/dt)[(ct,r)] = γ(cdt/dt,dr/dt) = γ(c,u) = U
U = (U·∂)[R] = (U·∂[R]) = U^αη_αβ∂^β[R^μ] = U^αη_αβη^βμ = U^αδ_α^μ = U^μ = U
=============================

A = dU/dτ = (U·∂)[U]
4-Acceleration is the derivative of 4-Velocity wrt. Proper Time τ.
A = dU/dτ = γdU/dt = γ(d/dt)[γ(c,u)] = γ(d/dt)[(γc,γu)] = γ((d/dt)[γc],(d/dt)[γu]) = γ(cγ', γ'u + γu̇) = A
A = (U·∂)[U] = (U·∂[U]) = U^αη_αβ∂^β[U^μ]
= U^αη_αβ[[∂_t/c (γc), ∂_t/c (γu)],[-∇(γc), -∇(γu)]]
= U^α[[∂_t/c (γc), 0],[0,∇(γu)]]
= γ(c∂_t/c (γc), u·∇(γu))
= γ(c∂_t(γ), d/dt (γu))
= γ(cγ', γ'u + γu̇) = A^μ = A
=============================

U·dU/dτ = U·A = 0
T·dT/dτ = 0
The 4-Acceleration of an Event is always orthogonal to the 4-Velocity of that same Event.
Basically, the 4-Velocity is tangent to the worldline, and the 4-Acceleration is normal to the worldline.
T·T = (1)²
U·U = (c)²
d/dτ[U·U] = d/dτ[(c)²] = 0
d/dτ[U·U] = d/dτ[U]·U +U·d/dτ[U] = A·U + U·A = 2*(U·A) = 0, hence (U·A) = 0
4-Velocities are time-like and 4-Accelerations are space-like.
see the "Invariant Rest Value of the Temporal Component Rule"
=============================

U₁·U₂ = γ₁₂(c²) = γ_rel(c²)	U·U = (c)²
T₁·T₂ = γ₁₂ = γ_rel	T·T = 1

When measuring two different 4-Velocities, the Lorentz Scalar Product is proportional to their relative Lorentz gamma factor γ₁₂ = γ_rel.
The Lorentz Scalar Product U₁·U₂ = γ₁(c,u₁)·γ₂(c,u₂) = γ₁γ₂(c² - u₁·u₂) = γ₂(c²){when u₁ = 0} = γ₁(c²){when u₂ = 0} = γ₁₂(c²) = γ_rel(c²)
γ₁γ₂(c² - u₁·u₂) = γ_rel(c²)
One also gets the relativistic "addition" of velocities with this:
γ[u₁]γ[u₂](c²-u₁·u₂) = γ[u_rel]c²
γ₁γ₂(c²-u₁·u₂) = γ_relc²
γ₁γ₂(1-β₁·β₂) = γ_rel
γ₁^-2γ₂^-2(1-β₁·β₂)^-2 = γ_rel^-2
(1-β₁·β₁)(1-β₂·β₂)(1-β₁·β₂)^-2 = (1-β_rel·β_rel)
(β_rel·β_rel) = 1-(1-β₁·β₁)(1-β₂·β₂)(1-β₁·β₂)^-2
(β_rel)² = [(1-β₁·β₂)²-(1-β₁·β₁)(1-β₂·β₂)](1-β₁·β₂)^-2
(β_rel)² = [(β₁)²-2(β₁·β₂)+(β₂)²](1-β₁·β₂)^-2
(β_rel)² = [(β₁)-(β₂)]²(1-β₁·β₂)^-2
β_rel = [β₁-β₂]/(1-β₁·β₂)
u_rel = [u₁-u₂]/(1-β₁·β₂)
or, by letting u₂ --> -u₂ (β₂ --> -β₂)
u_rel = [u₁+u₂]/(1+β₁·β₂) = [u₁+u₂]/(1+u₁·u₂/c²) : The relativistic composition of velocities law

Also, the definition of the Lorentz Gamma Factor is contained in this.
U·U = γ(c,u)·γ(c,u) = γ²(c² - u·u) = (c²)
Hence:
γ²(c² - u·u) = (c²)
γ² = (c²)/(c² - u·u)
γ² = 1/(1 - u·u/c² ) = 1/(1 - β·β)
γ = 1/√[1 - u·u/c² ] = 1/√[1 - β·β]
=============================

N = N_f = n_oU = (N/V_o)U
4-NumberFlux N is the Rest NumberDensity n_o times the 4-Velocity.
N = n_oU = n_oγ(c,u) = γn_o(c,u) = n(c,u) = (nc,nu)
*Not to be confused with the 4-Null N*
This can be measured in SR fluid and dust experiments, with number density and number flux related in a manner similar to time and space.
The Invariant Count of Particle #, the Lorentz Scalar N = n_oV_o = nV
The Rest NumberDensity is used to make other important 4-Vectors and Lorentz Scalars, significantly, the Lorentz Scalar Lagrangian Density L_deno = -n_o(P_T·U)
Effectively, any "particle-type" 4-Vector can be transformed into a "density-type" 4-Vector by multiplying by the rest number density n_o.
The 4-NumberFlux N can be used in generating the Stress-Energy Tensor for SR Dust
T_dust^μν = P^μN^ν = m_oU^μn_oU^ν = m_on_oU^μU^ν = ρ_moU^μU^ν = ρ_moc²T^μT^ν = ρ_eoT^μT^ν = ρ_eoV^μ^ν
A flux is a <charge> density*velocity. SI Units [<charge>/m³] * [m/s] = [<charge>/m²·s].
A Flux 4-Vector is a Lorentz Scalar <charge> * 4-NumberFlux N., which is equal to a <charge-density> * 4-Velocity U.
<charge> * N = <charge> * n_o * U = <charge-density> * U
=============================

	Particle Count	Mass_Energy	(d/dτ)[Mass_Energy]	Entropy	EM Charge	WaveAngFreq	EM Potential
(Lorentz Scalar) <Potential>	Ω = -X·U (free worldline)	S_act= -X·P (free particle action)				Φ = -X·K (free wave phase)
-d/dτ[<Potential>] <Charge>*c²	U·U = c²	E_o = U·P = -U·∂[S] = -d/dτ[S] E_o = m_oc²				ω_o = U·K = -U·∂[Φ] = -d/dτ[Φ] ω_o = (ω_o/c²)c²
<Charge>	N (usually 1)	m_o = (E_o/c²)	(d/dτ)[m_o]	S_ent	q	(ω_o/c²)	(φ_o/c²)
Particle 4-Vector <Charge>U	U	P = -∂[S] P = m_oU = (E_o/c²)U	F = (d/dτ)[m_o]U + m_oA		J_q = qU	K = -∂[Φ] K = (ω_o/c²)U	A = (φ_o/c²)U
Density 4-Vector Flux 4-Vector <Charge>N <ChargeDensity>U	N = U_den = n_oU	G = P_den = n_oP G = u_moU = m_on_oU = m_oN G = U·T^μν/c²	F_d = F_den = n_oF F_d = -∂·T^μν	S = s_oU = S_entn_oU = S_entN	J = J_qden = n_oJ_q J = ρ_oU = qn_oU = qN	? = (ω_o/c²)N	? = (φ_o/c²)N
<ChargeDensity>	n_o	u_mo = (u_eo/c²) = n_om_o	(d/dτ)[u_mo]	s_o = n_oS_Ent	ρ_o = n_oq	n_o(ω_o/c²)	n_o(φ_o/c²)
4-Divergence = 0 Conservation Law	∂·N = 0 Conservation of Particle Count N	∂·G = 0 Conservation of Mass_Energy m_o	∂·F_d = 0 Conservation of Power??	∂·S = 0 Conservation of Entropy S_ent	∂·J = 0 Conservation of Charge q	∂·K = 0 Conservation of Wave_Freq?	∂·A = 0 Conservation of EM Potential (Lorenz Gauge)

=============================

P = m_oU = (E_o/c²)U {massive case}
P = (|p|)N {massless = photonic case, |p| is a "momentum intensity", N is the 4-Null, not the 4-NumberFlux}
One of the more important relations, the 4-Momentum is related to the 4-Velocity by its rest mass.
(E/c,p) = m_oγ(c,u) = γm_o(c,u) = m(c,u) = (mc,mu) {massive case}
(E/c,p) = |p|(1,n̂) = (|p|,|p|n̂) = (|p|,p) {massless case}
4-Momentum is the Rest Mass m_o times the 4-Velocity, or the "momentum intensity" |p| times the 4-Null.
This can be measured in SR collision experiments.
E = mc² = γm_oc²: Einstein's famous equation relating energy and mass.
E_o = m_oc²
p = mu = γm_ou
Relativistic energy E = γE_o = γm_oc² = mc² = √[(m_oc²)² + (|p|c)²] = √[(E_o)² + (|p|c)²] : All of these are equivalent formulations.
Relativistic 3-momentum p = γm_ou = mu = (E/c²)u = (γE_o/c²)u : All of these are equivalent formulations.
=============================

P_den = G = n_oP = n_om_oU = (n_oE_o/c²)U = ρ_moU = U_νT^μν/c²
The 4-MomentumDensity G = (E_den/c,p_den) = (u_e/c,g) = (u_e/c,s/c²) = can be obtained by multiplying by the scalar invariant rest number density (n_o).
When the scalar invariant # of particles N = 1, this is the equivalent of dividing by the scalar invariant rest volume (V_o)
N = n_oV_o
Start with Energy-Momentum Stress Tensor of a perfect fluid (Rest Energy Density ρ_eo, Rest Pressure p_o):

Traditional Style	Projection Tensor Style
T_perfectfluid^μν = (ρ_eo + p_o)U^μU^ν/c² - p_oη^μν	T_perfectfluid^μν = (ρ_eo)V^μν - (p_o)H^μν
Contract with the 4-Velocity	Contract with the 4-Velocity
T^μνU_ν = (ρ_mo + p_o/c²)U^μU^νU_ν - p_oη^μνU_ν	T^μνU_ν = (ρ_eo)V^μνU_ν - (p_o)H^μνU_ν
T^μνU_ν = (ρ_mo + p_o/c²)U^μc² - p_oU^μ	T^μνU_ν = (ρ_eo)U^μ - (p_o)(0^μ)
T^μνU_ν = (c²ρ_mo + p_o)U^μ - p_oU^μ	T^μνU_ν = (ρ_eo)U^μ
T^μνU_ν = c²ρ_moU^μ	T^μνU_ν = c²ρ_moU^μ
T^μνU_ν = c²G^μ = c²G	T^μνU_ν = c²G^μ = c²G

ρ_eo = u_e = E_den = EnergyDen, s/c² = p_den = EnergyFlux = uU = c²g
s_EM = s = s_e = (e x b)/μ_o = (e x h) = c²p_den = PoyntingVector
u_EM = u_e = (e·ε_oe + b·b/μ_o)/2 = (e·d + b·h)/2 = EM energy density, where d = ε_oe, and h = b/μ_o
T^μν{EM / no restframe / null} =

c²ρ_mo = ρ_eo = (1/2)ε_o(e² + c²b²)	cg = cε_o(e x b)
cg = cε_o(e x b)	σ^ij = -ε_o[eⁱe^j + c²bⁱb^j - (1/2)δ^ij(e² + c²b²)]

=============================

∂·P_{den_tot} = (∂_t/c,-∇)·(E_{den_tot}/c,p_{den_tot}) = (∂_tE_{den_tot} + ∇·p_{den_tot}) = 0
∂·P_{den_tot} = ∂_t(u_m + u_e) + ∇·(s_m + s_e) = 0
The Generalized Poynting Theorem where P_{den_tot} is the total 4-Momentum Density of the system in question.
The (_m) values correspond to matter, and the (_e) to EM fields.
It is only the combination of all sources/sinks that is conserved.
u = E_den = EnergyDen, s = p_den = EnergyFlux = PoyntingVector = uU = c²g
u_EM = u_e = (e·ε_oe + b·b/μ_o)/2 = (e·d + b·h)/2 = EM energy density, where d = ε_oe, and h = b/μ_o
s_EM = s = s_e = (e x b)/μ_o = (e x h) = c²p_den = PoyntingVector
ε_oμ_o = 1/c²
T^μν{EM / no restframe / null} =

c²ρ_mo = ρ_eo = (1/2)ε_o(e² + c²b²)	cg = cε_o(e x b)
cg = cε_o(e x b)	σ^ij = -ε_o[eⁱe^j + c²bⁱb^j - (1/2)δ^ij(e² + c²b²)]

=============================

J = ρ_oU = qn_oU = qN
(ρc,j) = ρ_oγ(c,u) = γρ_o(c,u) = ρ(c,u) = (ρc,ρu)
(ρc,j) = qn_oγ(c,u) = qγn_o(c,u) = qn(c,u) = q(nc,nu)
<charge> * N = <charge> * n_o * U = <charge-density> * U
4-CurrentDensity is the Rest ChargeDensity (qn_o = ρ_o) times the 4-Velocity, where (q) is a particle charge.
This can be measured in SR-EM experiments, with charges and currents related in a manner similar to time and space.
For a moving point charge, the density is given by a delta function:
(ρc,j) = qn_oγ(c,u) = qγn_o(c,u) = qn(c,u) ~ qδ³(r - r')(c,u)
=============================

J = (ρ_o/m_o)P = (qn_o/m_o)P or P = (m_o/ρ_o)J
It is derivable from the SR relations P = m_oU = (E_o/c²)U and J = ρ_oU
Since both P and J are Lorentz Scalar proportional to U, then by the mathematics of tensors J must be Lorentz Scalar proportional to P.
(i.e. Tensors obey mathematical transitivity, or in this case they are also Right Euclidean {if a~c and b~c, then a~b} )
J = ρ_oU = (ρ_o)/(m_o)P = (ρ_o/m_o)P = (γρ_o/γm_o)P = (ρ/m)P
=============================

Σ*[P_n] = Z = (0,0)
The Conservation of 4-Momentum. Let me repeat: The Conservation of 4-Momentum.
Possibly one of the most important concepts in all of physics.
The 4-Vector notation hence combines the Newtonian separate notions of Conservation of Energy and Conservation of 3-momentum.
The summation Σ* counts all pre-collision terms positively and post-collision terms negatively.
The sum of the 4-momenta of all particles going into a point collision is equal to the sum of the 4-momenta of all particles going out.
Since P = (E/c,p) = (mc,p) = (mc,mu) we get the temporal eqn. { Σ*[m_nc] = cΣ*[m_n] = 0 } and the spatial eqns. { Σ*[m_nu_n] = 0 }
=============================

P₁ + P₂ = P₁' + P₂': Conservation of 4-Momentum
P₁·P₂ = P₁'·P₂': The Elastic Collision Lemma
4-TotalMomentum P_T_sys = Σ_n[P_T_particle(n)], meaning that the total momentum of a system is the sum of all particle momenta in the system
The Elastic Collision Lemma, a consequence of the Conservation of 4-Momentum.
Two particles 1 and 2 with interaction, a collision, whereby some energy/momentum could be transferred from one to the other.
Let the unprimed terms be pre-collision, and the primed terms be post-collision.
P₁ + P₂ = P₁' + P₂': from Conservation of 4-Momentum
(P₁ + P₂)² = (P₁' + P₂' )²
P₁·P₁ + 2P₁·P₂ + P₂·P₂ = P₁'·P₁' + 2P₁'·P₂' + P₂'·P₂'
but P₁·P₁ = P₁'·P₁' = (m_o1c)² and P₂·P₂ = P₂'·P₂' = (m_o2c)²
so, those terms can cancel from both sides, leaving...
2P₁·P₂ = 2P₁'·P₂'
P₁·P₂ = P₁'·P₂'
There is an invariant in the relative 4-Momenta when the particle types don't change (they keep the same rest masses).
=============================

F = dP/dτ = (U·∂)[P] = (d/dτ)[P] = (d/dτ)[m_oU] = (d/dτ)[m_o]U + m_o(d/dτ)[U] = (d/dτ)[m_o]U + m_oA
F = dP/dτ = γdP/dt = γ(d/dt)[(E/c,p)] = γ(dE/cdt,dp/dt) = γ(Ė/c,ṗ) = γ(Ė/c,f)
4-Force is the derivative of 4-Momentum wrt. Proper Time τ.
A pure 4-Force is one that has constant rest mass {(d/dτ)[m_o] = 0}, in which case F_p = m_oA{pure = space-like} and 4-ForcePure F_p = γ(u·f/c,f)
An example of a pure 4-Force is the ElectroMagnetic field, which has 4-Force_EM F_EM = γq( (u·e)/c, (e) + (u⨯b) )
A heat-like 4-Force is one that has (A = 0), in which case F_h = (d/dτ)[m_o]U{heat-like = time-like} and 4-ForceHeat F_h = γ²ṁ_o(c,u) = γṁ(c,u)
A scalar-based 4-Force is one that has (Ė = k(d/dτ)[Φ]), in which case F_s = k ∂[Φ]) {scalar} and 4-ForceScalar F_s = k(∂_t[Φ],-∇[Φ])
=============================

N = N_f = n_oU = U_den
The 4-NumberFlux can be obtained by multiplying by the scalar invariant rest number density (n_o).
When the Scalar Invariant ( # of particles N = 1 ), this is the equivalent of dividing by the scalar invariant rest volume (V_o)
n_o = N/V_o
N = n_oV_o = nV
Based on this, the 4-NumberFlux can be viewed as a 4-VelocityDensity
=============================

F_den = n_oF
The 4-ForceDensity can be obtained by multiplying by the scalar invariant rest number density (n_o).
When the Scalar Invariant ( # of particles N = 1 ), this is the equivalent of dividing by the scalar invariant rest volume (V_o)
n_o = N/V_o
N = n_oV_o = nV
An example is the 4-EM Force Density F_EMden^μ = dP_EMden^μ/dτ = J_νF^μν
=============================

F·U = γ_f(Ė/c,f)·γ_u(c,u) = γ_f γ_u (Ė - f·u) = γ_f Ė_o = γ_fṁ_oc²
If { F·U = 0} then {Ė_o = 0} and {(Ė - f·u) = 0} then {Ė = f·u} then 4-ForcePure F_p = γ(u·f/c,f)
This is true when there is no change in rest mass (rest energy E_o) of a test particle, or again, when the force is conservative or pure.
(i.e. The force is applied to a particle of stable invariant rest mass m_o)
We will find that the EM field is a pure force:
Ė = dE/dt = q(u·e)
f = dp/dt = q{(e) + (u⨯b)}
f·u = q{(e·u) + (u⨯b)·u} = q{(e·u) + (0)} = q(u·e)
4-Force_EMF_EM = γq( (u·e)/c, (e) + (u⨯b) )
and hence,F_EM·U = 0 {for an EM field, it is conservative}
see the "Invariant Rest Value of the Temporal Component Rule"
=============================

P·U = (E/c,p)·γ(c,u) = γ(E - p·u) = E_o
P·U = m_oU·U = m_oc² = E_o
The Scalar Product of the 4-Momentum with the 4-Velocity gives the Invariant Rest Energy.
see the "Invariant Rest Value of the Temporal Component Rule"
=============================

A_EM·U = (φ/c,a)·γ(c,u) = γ(φ - a·u) = φ_o
A_EM·U = (φ_o/c²)U·U = (φ_o/c²)c² = φ_o
The Scalar Product of the 4-EM-VectorPotential with the 4-Velocity gives the Invariant Rest Scalar Potential.
see the "Invariant Rest Value of the Temporal Component Rule"
=============================

J·U = (ρc,j)·γ(c,u) = γ(ρc² - j·u) = ρ_oc²
J·U = ρ_oU·U = ρ_oc²
The Scalar Product of the 4-CurrentDensity with the 4-Velocity gives the Invariant Rest Charge Density times speed-of-light squared.
see the "Invariant Rest Value of the Temporal Component Rule"
=============================

K·U = (ω/c,k)·γ(c,u) = γ(ω - k·u) = ω_o
K·U = (ω_o/c²)U·U = (ω_o/c²)c² = ω_o
The Scalar Product of the 4-WaveVector with the 4-Velocity gives the Invariant Rest Angular Frequency.
see the "Invariant Rest Value of the Temporal Component Rule"
=============================

N·U = n(c,u)·γ(c,u) = γn(c² - u·u) = nc²/γ = n_oc²
N·U = n_oU·U = n_oc²
The Scalar Product of the 4-NumberFlux with the 4-Velocity gives the Invariant Rest Number Density times speed-of-light squared.
see the "Invariant Rest Value of the Temporal Component Rule"
=============================

K = (ω_o/c²)U
4-WaveVector is the Rest AngularFrequency over lightspeed squared (ω_o/c²) times the 4-Velocity.
A massive wave has a non-zero rest-angular-frequency.
A wave "at rest" is simply a standing wave in time.
The relation can be generated by looking at the previous Scalar Product relations.
U·U = (c)²
K·U = (ω_o)
K·K = (ω_o/c)²
hence:
K = (ω_o/c²)U = (ω/c,k) = (ω_o/c²)γ(c,u) = γ(ω_o/c²)(c,u) = (γω_o/c, γω_ou/c²) = (ω/c, ωu/c²) = (ω/c, ωn̂/v_phase)
The wave can move, with the relation:
(|u * v_phase| = c²)
(|v_group* v_phase| = c²)
The 4-WaveVector can be measured in SR wave experiments, especially those involving the Doppler Effect.
The 4-Velocity of a massless 4-WaveVector is not well-defined.
K = (ω_o/c²)U → (0)U
However, K_massless remains well-defined because (ω = γω_o).
The Lorentz Gamma Factor (γ) goes to infinity and the Rest Frequency (ω_o) goes to zero in such a way that (ω) remains finite.
K = (ω_o/c²)U = (ω_o/c²)γ(c,u) = (γω_o/c²)(c,u) = (ω/c²)(c,u) = (ω/c)(1,β)
K = (ω/c)(1,β)
K_massless = (ω/c)(1,n̂)
----------------------------

Relativistic Doppler Effect (derivation using 4-Vectors)
K = (k⁰,k), a generic SR 4-Vector under observation, relative to observer (*note*, for the derivation this is not necessarily the 4-WaveVector)
K·U = a Lorentz invariant, upon which all observers agree, see the "Invariant Rest Value of the Temporal Component Rule"
take K·U→ K·U_o = (k⁰,k)·(c,0) = ck⁰ = the value of the temporal component of K as seen by observer U
now, let there be an observer U_obs at rest and an emitter U_emit moving with respect to U_obs
U_obs = (c,0): 4-Velocity of observer at rest
U_emit = γ(c,u): 4-Velocity of emitter relative to observer
---------
K·U_obs = (k⁰,k)·(c,0) = c k⁰ = ck⁰_{_obs} = invariant
K·U_emit = (k⁰,k)·γ(c,u) = γ(ck⁰ - k·u) = ck⁰_{_emit} = invariant
---------
K·U_obs/K·U_emit = ck⁰_{_obs}/ck⁰_{_emit} = k⁰_{_obs}/k⁰_{_emit} = invariant
K·U_obs/K·U_emit = ck⁰/γ(ck⁰ - k·u) = 1 /γ(1 - k·u/k⁰c) = 1 /γ[1 - (|k|/k⁰)*(n̂·u/c)] = invariant
---------
k⁰_{_obs} = k⁰_{_emit}/γ(1 - (|k|/k⁰)*(n·u/c))
= k⁰_{_emit}/γ(1 - (|k|/k⁰)*(n·β))
= k⁰_{_emit}/γ(1 - (|k|/k⁰)*(β cos[θ]))
---------
Up to this point, the derivation is general and could be for any 4-Vector K
Now, I am going to assume that K actually is the 4-WaveVector for the rest of the derivation.
K = (ω/c,k)
k⁰_{_obs} = k⁰_{_emit}/γ(1 - (|k|/k⁰)*(n̂·β))
ω_{_obs}/c = ω_{_emit}/cγ(1 - (c|k|/ω)*(n̂·β))
ω_{_obs} = ω_{_emit}/γ(1 - (c|k|/ω)*(n̂·β))
ω_{_obs} = ω_{_emit}/γ(1 - (c/v_phase)*(n̂·β))
ω_{_obs} = ω_{_emit}/γ(1 - (n̂·u)/v_phase) {for photons or massive particles, with ( u ) as the relative velocity between emitter and observer, and v_phase is the emission wave velocity}
ω_{_obs} = ω_{_emit}/γ(1 - (|u|/v_phase)cos[θ]) {for photons or massive particles, with ( u ) as the relative velocity between emitter and observer, and v_phase is the emission wave velocity}
---------
If K is photonic/light-like/null, then (v_phase = c), which gives the Relativistic Doppler Formula for photonic particles
ω_{_obs} = ω_{_emit}/γ(1 - (n̂·u)/c) {for photonic}
ω_{_obs} = ω_{_emit}/γ(1 - (n̂·β)) {for photonic}
ω_{_obs} = ω_{_emit} √[1 + |β|]√[1-|β|] /(1 - (n̂·β)) {for photonic}
------------
In the way things are defined, n̂ is unit direction of the photon emission; it always points from the emitter to the observer.
For motion of source away from observer, (n·β) = -β, so ω_obs = ω_emit/γ(1 + β) = ω_emit*√[1-β]/√[1 + β] = RedShift
For motion of source toward the observer, (n·β) = + β, so ω_obs = ω_emit/γ(1 - β) = ω_emit*√[1 + β]/√[1-β] = BlueShift
For motion of source tangent to the observer, (n·β) = 0, so ω_obs = ω_emit/γ(1 - 0) = ω_emit/γ = Transverse Doppler Shift

There is also a formula for aberration, and a link between Doppler Shift and Aberation.
ω sin[θ] = ω_o sin[θ_o]
=============================

K = (ω_o/E_o)P or P = (E_o/ω_o)K
It is derivable from the SR relations K = (ω_o/c²)U and P = m_oU = (E_o/c²)U
Since both P and K are Lorentz Scalar proportional to U, then by the mathematics of tensors K must be Lorentz Scalar proportional to P.
(i.e. Tensors obey mathematical transitivity, or in this case they are also Right Euclidean {if a~c and b~c, then a~b} )
K = (ω_o/c²)U = (ω_o/c²)/(E_o/c²)P = (ω_o)/(E_o)P = (ω_o/E_o)P = (γω_o/γE_o)P = (ω/E)P
Now then, I wonder if there is anything interesting about E/ω... Hmmmmm...
=============================

K·X = (ω/c,k)·(ct,x) = (ωt - k·x) = -Φ
The Phase Φ of an SR Wave (represented by the 4-WaveVector K) is a Lorentz Scalar.
See the Scalar Product-Gradient-Position Relation.
=============================

K = -∂[Φ]
The 4-WaveVector can be derived in terms of periodic motion, for which families of surfaces move through space as time increases,
or alternately,as families of hypersurfaces in SpaceTime, formed by all events passed by the wave surface.
The 4-WaveVector is everywhere in the direction of propagation of the wave surfaces.
More specifically, any particular 4-WaveVector K is the vector orthogonal to a hypersurface of constant phase Φ at that SpaceTime point/event.
{Each hypersurface is an ensemble of events E(t,x,y,z) that all share the same value of Φ }
The function that provides a vector orthogonal to a surface at each point is the 4-Gradient.
i.e. K = -∂[Φ].
The phase is chosen so that it decreases by unity (1 cycle or 2π radians) as we pass from one wave crest to the next, in the direction of propagation of the waves.
See Rindler, "Introduction to Special Relativity 2nd.Ed.", sec.24 Wave motion
=============================

K·U = (ω/c,k)·γ(c,u) = γ(ω - k·u) = U·K = U·∂[-Φ] = d/dτ[-Φ] = ω_o
The derivative of the phase (Φ) wrt. Proper Time is the negative rest frequency (-ω_o)
K·X = (ω/c,k)·(ct,x) = (ωt - k·x) = -Φ
Φ = -K·X
d/dτ[Φ] = γd/dt[Φ] = γd/dt[-K·X] = γd/dt[-(ωt - k·x)] = γ[-(ω - k·u)] = -(1)(ω_o - k·0) = -ω_o
d/dτ[Φ] = d/dτ[-K·X] = -(K·U) = -ω_o
=============================

∂[K] = [[0]] = 0^μν
U·∂[K] = d/dτ[K] = Z = 0^μ
The 4-Gradient of the 4-WaveVector is the zero matrix assuming the 4-WaveVector is not a function of 4-Position.

∂[K] = ∂^uK^v = (∂t/c,-∇)(ω/c,k) =

[∂_t/c[ω/c], ∂_t/c[k]]
[-∇[ω/c], -∇[k]]

= [[0]]

This would be the case if a particle "carries" K, and it only changes via interaction with other particles.
This makes sense. K is proportional to U, via K = (ω_o/c²)U, and the particle simply "carries" U until it interacts with another particle or field.
This is confirmed in double-slit experiments - even though it travels through slits as a wave, it is detected as discrete particles at the screen.
=============================

∂[K·X] = ∂[-Φ] = ∂^w[η_uvK^uX^v] = ∂^w[K_vX^v] = K_v∂^w[X^v] + X^v∂^w[K_v] = K_vη^wv + [0] = K^w = K·∂[X] + ∂[K]·X = K
Just more SR Mathematics - The 4-WaveVector K is the 4-Gradient of the SR Phase Φ (a Lorentz Invariant itself),
again assuming the 4-WaveVector is not a function of 4-Position.
=============================

∂·S = (∂_t/c,-∇)·(sc,s) = (∂_ts + ∇·s) = ? = 0
∂·S_perfectfluid = 0
The 4-Gradient Lorentz Product with the 4-EntropyFlux S = s_oU is zero, or that the Divergence of the 4-EntropyFlux is zero, for a conserved field.
There are no sources or sinks of 4-EntropyFlux when this is true. This is related to the Conservation of Entropy S_ent.
The divergence formula may actually be applied in several other circumstances regarding Conserved quantities.
We will see more about relativistic Perfect Fluids later, but here is the proof for Conservation of 4-EntropyFlux.
We need to setup a few equations first:

The Fundamental Thermodynamic Equation:
E_o = TS_o - PV_o + μN_o
Divide everything by RestVolume V_o
[E_o = TS_o - PV_o + μN_o]/V_o
E_o/V_o = TS_o/V_o - PV_o/V_o + μN_o/V_o
ρ_eo = Ts_o - P + μn_o
Local Thermodynamic Densities{ ρ_eo + P = Ts_o + μn_o = h_o } where (h_o) is the enthalpy density

U = γ(c,u), P = (E/c,p), U·U = c²,P·P = (m_oc)²
U·P = γ(c E/c-u·p) = γ(E-u·p) = E_o = γ(T S - PV +μ N) = (T_oS_o - P_oV_o + μ_oN_o)
U·P = γ(E-u·p) = E_o = (T_oS_o - P_oV_o + μ_oN_o) = m_oc² for a spatially homogeneous system: relativistic Gibbs-Duhem eqn.

Invariants	P = Pressure = P_o	N = ParticleNum = N_o	S = Entropy = S_o
Variables	V = Volume = (1/γ)V_o	μ = ChemPoten = (1/γ)μ_o	T = Temperature = (1/γ)T_o

V*P(particle superstructure = Vol*Press)
μ*N (particle structure = ChemPoten*ParticleNum)
T*S (particle substructure = Temp*Entropy)

The Gibbs-Duhem equation :
s_o∂_μ[T] + n_o∂_μ[μ] = ∂_μ[P]
U^μs_o∂_μ[T] + U^μn_o∂_μ[μ] = U^μ∂_μ[P]
{ S^μ∂_μ[T] + N^μ∂_μ[μ] = U^μ∂_μ[P] }

The 4-Velocity has a fixed magnitude in SR
U^νU_ν = c²
∂_μ[c²] = ∂_μ[U^νU_ν] = 2U_ν∂_μ[U^ν] = 0
{ U_ν∂_μ[U^ν] = 0 }

*Note* {The (μ) = Chemical Potential and the (^μ) = tensor index are totally different things, I need to change to a different tensor index when I get a chance}
T_perfectfluid^μν =
= (ρ_eo + P)U^μU^ν/c² - Pη^μν
= (Ts_o + μn_o)U^μU^ν/c² - Pη^μν
= (Ts_oU^μ + μn_oU^μ)U^ν/c² - Pη^μν
= (TS^μ + μN^μ)U^ν/c² - Pη^μν

∂_μT_perfectfluid^μν = 0^ν
U_ν∂_μT_perfectfluid^μν = U_ν0^ν = 0
= U_ν∂_μ[(TS^μ + μN^μ)U^ν/c² - Pη^μν]
= U_ν∂_μ[(TS^μ + μN^μ)]U^ν/c² + { (TS^μ + μN^μ)U_ν∂_μ[U^ν]/c²}- U_ν∂_μ[Pη^μν]
= U_ν∂_μ[(TS^μ + μN^μ)]U^ν/c² + { 0 } - U_ν∂_μ[Pη^μν]
= U_ν∂_μ[(TS^μ + μN^μ)]U^ν/c² - U_ν∂_μ[Pη^μν]
= ∂_μ[(TS^μ + μN^μ)]U_νU^ν/c² - η^μνU_ν∂_μ[P]
= ∂_μ[(TS^μ + μN^μ)] - U^μ∂_μ[P]
= ∂_μ[T]S^μ + T∂_μ[S^μ] + ∂_μ[μ]N^μ + μ∂_μ[N^μ] - U^μ∂_μ[P]
= T∂_μ[S^μ] + μ∂_μ[N^μ] + { S^μ∂_μ[T] + N^μ∂_μ[μ] - U^μ∂_μ[P] }
= T∂_μ[S^μ] + μ∂_μ[N^μ] + { 0 }
= T∂_μ[S^μ] + μ∂_μ[N^μ]
= T ∂·S + μ ∂·N
= 0
If the Particle # is conserved (∂·N = 0), then (T ∂·S = 0)
============================

∂·J = (∂_t/c,-∇)·(ρc,j) = (∂_tρ + ∇·j) = ? = 0
∂·J_EM = 0
The 4-Gradient Lorentz Product with the 4-CurrentDensity J = ρ_oU is zero, or that the Divergence of the 4-CurrentDensity is zero, for a conserved field.
There are no sources or sinks of 4-CurrentDensity when this is true. This is related to the Conservation of Charge/Current and Noether's Theorem.
The divergence formula may actually be applied in several other circumstances regarding Conserved quantities.
Due to the way it is defined, the 4-Divergence of the 4-CurrentDensity of an EM field is 0, and thus conservative. We will see this a bit later.
=============================

∂·U = (∂_t/c,-∇)·γ(c,u) = ( ∂_tγ + ∇·[γU] ) = ( ∂_tγ + γ(∇·u) + (u·∇[γ] ) ) = ? = 0
The 4-Gradient Lorentz Product with the 4-Velocity U is zero, or that the Divergence of the 4-Velocity is zero, for a conserved field.
There are no sources or sinks of 4-Velocity when this is true.
This is related to the Conservation of Charge and Noether's Theorem.
If ( ∂_tγ ) = 0 then the flow is constant or inertial.
If ( ∇·u) = 0 then the flow is incompressible, in which case (u) is said to be solenoidal.
If ( u·∇[γ] ) = 0 then the flow is steady, in which case (γ) is constant along a streamline.
If an incompressible flow also has a curl of zero, so that it is also irrotational, then the flow velocity field is Laplacian.
The divergence formula may actually be applied in several other circumstances regarding Conserved quantities.
Note the following: ∂·J = 0 = ∂·[ρ_oU] = ρ_o∂·U + U·∂[ρ_o] = 0
For point particles, the charge density is non-zero, the change in charge density ∂[ρ_o] is zero, hence it is the (∂·U) = 0.
If the 4-Velocity U is a conservative field, then any of the other 4-Vectors which are just a Lorentz Scalar times the 4-Velocity will be conserved.
∂·U = (∂_t/c,-∇)·γ(c,u) = ( ∂_tγ + ∇·[γU] ) = ( ∂_tγ + γ(∇·u) + (u·∇[γ] ) ) = 0
ρ_o(∂·U) = ρ_o(∂_t/c,-∇)·γ(c,u) = (∂_t/c,-∇)·γρ_o(c,u) = (∂_t/c,-∇)·ρ(c,u) = ( ∂_tρ + ∇·[ρU] ) = [ ∂_tρ + ρ(∇·u) + (u·∇[ρ] ) ] = 0

This is related to the Advection Equation and Incompressible Flow,
See Incompressible Euler Equations, General Continuity Equations, Conservation Form Equations.
Essentially this is the conservation of worldlines...
=============================

A_EM = (φ_o/c²)U
A_EM = (φ/c,a) = (φ_o/c²) γ(c,u) = ((γφ_o/c),(γφ_o/c²)u)
4-EM_VectorPotential is the Rest EM Scalar Potential φ_o over c squared times the 4-Velocity.
This can be measured in SR-EM experiments, with charges and currents related in a manner similar to time and space.
giving temporal component { φ = γφ_o} and spatial component { a = (γφ_o/c²)u}
This formula is for a generic 4-VectorPotential
For a point charge one can define:
The Rest EM Scalar Potential (φ_o) = (qc/4πε_o)/[R·U]_ret = (q/4πε_o)/[R·T]_ret is a Lorentz Scalar Invariant.
with [...]_ret impling retarded (R·R = 0, the definition of a light signal)
**Note** When the A is referring to a photonic wave, the rest potential φ_o is zero in exactly the same way the rest mass m_o of a photon is zero.
In the (photonic = light-like = null) situation, there is no "at-rest" frame.
=============================

A_{EMpointcharge} = (q/4πε_oc)U/[R·U]_ret = (qμ_oc/4π)U/[R·U]_ret {for a point charge q}
A_{EMpointcharge} = (q/4πε_oc²)U/[R·T]_ret = (qμ_o/4π)U/[R·T]_ret {for a point charge q}
A_EM= ∭(dV_o/4πε_oc²)J/[r]_ret
with [...]_ret impling retarded condition (R·R = 0, the definition of a light signal)
The 4-EM_VectorPotential of a moving point charge (Liénard-Wiechert Potential)
If we use the A_EM = (φ_o/c²)U definition and compare terms with above:
(φ_o/c²) = (q/4πε_oc) /[R·U]_ret
(φ_o) = (qc/4πε_o) /[R·U]_ret
(φ_o) = (qc/4πε_o) /[c²τ]_ret
(φ_o) = (q/4πε_o) /[cτ]_ret
(φ_o) = (q/4πε_o)/r {which is the correct potential for a point charge in its rest frame}
since R·R = (ct)² - |r|² = 0 → ct = r

And likewise, the scalar and vector potential of a moving point charge that was initially at rest.
φ = (γφ_o) = (γq/4πε_o) /r
a = (φ_o/c²)γU = (γφ_o/c²)u = (γφ_o/c²)u = (φ/c²)u = ((γq/4πc²ε_o) /r)u = ((γqμ_o/4π) /r)u
There is actually a more generic expression which is a bit more complicated, see Rindler.

We can actually simplify the expression a bit by using the 4-UnitTemporal T = U/c
(φ_o/c²) = (q/4πε_oc²) /[R·T]_ret
(φ_o) = (q/4πε_o) /[R·T]_ret
(φ_o) = (q/4πε_o) /[cτ]_ret
(φ_o) = (q/4πε_o)/r {which is the correct potential for a point charge in its rest frame}
since R·R = (ct)² - |r|² = 0 → ct = r

Jefimenko's equations from the retarded potentials:
φ[t,r] = (μ_o/4π)∫d³r' ρc²[t_r,r'] /|r - r'| = (1/4πε_o)∫d³r' ρ[t_r,r'] /|r - r'|
a[t,r] = (μ_o/4π)∫d³r' j[t_r,r'] /|r - r'|

combining into 4-Vector form:
(φ/c,a)[t,r] = (μ_o/4π)∫d³r' (ρc,j)[t_r,r'] /|r - r'|
A_EM[t,r] = (μ_o/4π)∫d³r' J[t_r,r'] /|r - r'|
A_EM[t,r] = (μ_o/4π)∫dτ J[t_r,r'] /τ

using the Green's function for the Laplace equation:
G(r,r') = -1/(4π)(1/|r - r'|) where (∇·∇)G(r,r') = δ⁽³⁾(r - r')

A_EM[t,r] = (μ_o)∫d³r' J[t_r,r'] G(r,r')
(∂·∂)A_EM - ∂(∂·A_EM) = μ_oJ

For a moving point charge, the density is given by a delta function:
J = (ρc,j) = ρ_oU = qn_oU = qn_oγ(c,u) = qγn_o(c,u) = qn(c,u) ~ qδ⁽³⁾(r - r')(c,u)

A_EM = (q/4πε_oc)U/[R·U]_ret
= (ρ_o/n_o)/4πε_oc)U/[R·U]_ret
= (1/n_o4πε_oc)J/[R·U]_ret
= (V_o/4πε_oc)J/[R·U]_ret
= ∭(dV_o/4πε_oc)J/[R·U]_ret
= ∭(dV_o/4πε_oc)J/[c²τ]_ret
= ∭(dV_o/4πε_oc)J/[cr]_ret
A_EM = ∭(dV_o/4πε_oc²)J/[r]_ret = ∭(dV_oμ_o/4π)J/[r]_ret = ∭(d³xμ_o/4π)J/[r]_ret = (μ_o/4π)∭d³x J/[r]_ret

= (1/n_o4πε_oc)J/[R·U]_ret
= (μ_oc/n_o4π)J/[R·U]_ret
= (μ_oc/n_o4π)J/[c²τ]_ret
= (μ_o/n_o4π)J/[cτ]_ret
= (μ_o/cn_o4π)J/[τ]_ret
= (1/cn_o)(μ_o/4π)J/[τ]_ret
??
A_EM[t,r] = (μ_o/4π)∫dτ J[t_r,r'] /τ

Take the temporal component
(φ/c) = ∭(dV_o/4πε_oc²)(ρc) /[r]_ret
(φ) = ∭(ρdV_o/4πε_o) /[r]_ret

see Liénard-Wiechert_potential, Retarded_potential, Jefimenko's_equations, Green's_function_for_the_three-variable_Laplace_equation, Magnetic Potential,
=============================

Q = qA.
The 4-PotentialMomentum Q is a charge (q) time the 4-VectorPotential A.
Typically this would be the EM charge, but could be any type of "<charge>".
Essentially, Potentials and Fields carry energy and momentum.
It is a way of statistically accounting for the effects of lots and lots of individual particles.
=============================

P_T = P + Q = P + qA_EM
The 4-TotalMomentum of a system can be split into the 4-Momentum of a Particle P + charge (q) times 4-VectorPotential A.
Essentially, we are examining a lone particle running around in a big field which can affect the particle.
Typically, this is for an 4-EM_VectorPotential, however it could be for any type of SR 4-VectorPotential P_T = P + qA
This is an alternate way of thinking about the Minimal-Coupling Rule, P = P_T - Q = P_T - qA_EM
=============================

∂^ν[P_T^μ] = q∂^μ[A_EM^ν] {for an EM system}
The 4-Gradient of the 4-TotalMomentum is related to the 4-Gradient of the 4-EMVectorPotential.
Roughly, the change in TotalMomentum, or the TotalForce, is the Gradient of a VectorPotential.
This is one case for which tensor notation is required, since the order of the indices is important when dealing with the 4-Gradient.
This little bit of magic combined with Conservation of 4-TotalMomentum is enough to derive the Faraday EM Tensor.
The fact that each is the gradient of a "field" leads to the idea of gauge fixing/choice of gauge.
Two known relativistically covariant gauges are:
∂·A = (∂_t/c,-∇)·(φ/c,a) = (∂_tφ/c² + ∇·a) = 0 : The Lorenz Gauge for Classical EM - Yes, Lorenz, not Lorentz.
X·A = (ct,x)·(φ/c,a) = (tφ - x·a) = 0 : The Fock-Schwinger Gauge (Relativistic Poincaré Gauge).
We will see how this works in the section on the Lorentz Force Equation.
=============================

F^μ = dP^μ/dτ = qU_ν(∂^μA_EM^ν - ∂^νA_EM^μ) = qU_νF^μν = (q/m_o)P_νF^μν
F = dP/dτ = {qU·F^μν}
F = (U·∂)P = {qU·F^μν}
F_den^μ = dP_den^μ/dτ = J_νF^μν
The Lorentz Force Equation for a charged particle in a EM field.
The 1st version is in single index tensor format.
The 2nd and 3rd versions are in a slightly ambiguous mix of 4-Vector and 2-index Tensor Format,
for which we see the "Invariant Rest Value of the Temporal Component Rule", just to emphasize that works similarly.
The 4th version is the 4-ForceDensity.
We can build this up from the idea that the 4-TotalMomentum is just the sum of the individual charged particle 4-Momentum and q*the SpaceTime field 4-EM_VectorPotential.
P_T = P + qA
P = P_T - qA
P^μ = P_T^μ - qA^μ
∂^ν[P^μ] = ∂^ν[P_T^μ] - ∂^ν[qA^μ]
∂^ν[P^μ] = q∂^μ[A^ν] - q∂^ν[A^μ]: This from the rule about the 4-Gradient on the 4-TotalMomentum ∂^ν[P_T^μ] = q∂^μ[A_EM^ν]
∂^ν[P^μ] = q(∂^μ[A^ν] - ∂^ν[A^μ])
U_ν∂^ν[P^μ] = qU_ν(∂^μ[A^ν] - ∂^ν[A^μ]): Note that { U_ν∂^ν = (U·∂) = d/dτ }
(U·∂)[P^μ] = qU_ν(∂^μ[A^ν] - ∂^ν[A^μ])
d/dτ[P^μ] = qU_ν(∂^μ[A^ν] - ∂^ν[A^μ])
F^μ = d/dτ[P^μ] = qU_ν(∂^μ[A^ν] - ∂^ν[A^μ]) = qU_νF^μν
*Note* Here (F^μ) is the 4-Force and (F^μν) is the EM Faraday Tensor.

One way to simplify this is to take one component at a time:
γf¹ = γf^x = qU_ν(∂¹[A^ν] - ∂^ν[A¹])
= qU₀{∂¹[A⁰] - ∂⁰[A¹]} + qU₁{∂¹[A¹] - ∂¹[A¹]} + qU₂{∂¹[A²] - ∂²[A¹]} + qU₃{∂¹[A³] - ∂³[A¹]}
= q(γc){(-∂^x)[φ/c] - (∂^t/c)[a^x]} + q(-γu_x){0} + q(-γu_y){(-∂^x)[a^y] - (-∂^y)[a^x]} + q(-γu_z){(-∂^x)[a^z] - (-∂^z)[a^x]}
= qγ{(-∂^x)[φ] - (∂^t)[a^x]) + (0) + (-u_y){(-∂^x)[a^y] - (-∂^y)[a^x]} + (-u_z){(-∂^x)[a^z] - (-∂^z)[a^x]}
= qγ{(-∂^x[φ] - ∂^t[a^x]) + (0) + (-u_y)(-∂^x[a^y] + ∂^y[a^x]) + (-u_z)(-∂^x[a^z] + ∂^z[a^x])}
= qγ{(e^x) + (0) + (-u_y)(-b^z) + (-u_z)(b^y)}
= qγ{(e^x) + (u⨯b)^x}
Thus, taking all components:
γf = qγ{(e^x) + (u⨯b)^x} + qγ{(e^y) + (u⨯b)^y} + qγ{(e^z) + (u⨯b)^z}

or, we can use the already worked out cells from the EM Faraday Tensor, in another section...
F^μ = d/dτ[P^μ] = qU_ν(∂^μ[A^ν] - ∂^ν[A^μ]) = qU_νF^μν
F^μ = qU_νF^μν
Fⁱ = qU_νF^iν = q[(U₀Fⁱ⁰) + (U₁Fⁱ¹) + (U₂Fⁱ²) + (U₃Fⁱ³)]
= q[(γc eⁱ/c) + (-γu_x* -ε_i1kb^k) + (-γu_y* -ε_i2kb^k) + (-γu_z* -ε_i3kb^k)]
= γq[(eⁱ) + (u_x*ε_i1kb^k) + (u_y*ε_i2kb^k) + (u_z*ε_i3kb^k)]
= γq[(eⁱ) + (u⨯b)ⁱ]

γf = γq{(e) + (u⨯b)}: The Lorentz Force Equation for fusing Electric (e) and magnetic (b) fields

4-Force F = γ(Ė/c,f) = γ(ṁc,f)
F = dP/dτ = {qU·F^μν}
If we look at the components we get: **Note** E = Energy

γ	[Ė/c]	= d/dτ	[E/c]	= qγ	[c]	·	[0	-eⁱ/c]	= qγ	[c0 + u·e*/c]
	[ f ]		[p]		[u]		[eⁱ/c	-ε_ijkb^k]		[e + u⨯b]

γĖ/c = dE/cdτ = γq(u·e/c)
γf = dp/dτ = γq{(e) + (u⨯b)}

Ė = dE/dt = q(u·e)
f = dp/dt = q{(e) + (u⨯b)}

F_EM = γq( (u·e)/c, (e) + (u⨯b) )

F_EMden = γn_oq( (u·e)/c, (e) + (u⨯b) )
= γρ_o( (u·e)/c, (e) + (u⨯b) )
= ρ( (u·e)/c, (e) + (u⨯b) )
= ( (ρu·e)/c, ρ(e) + (ρu⨯b) )
F_EMden = ( (j·e)/c, ρ(e) + (j⨯b) )

In a rest frame:
F_EMo = q(0,e)
=============================

J^μ - (1/c²)(U_νJ^ν)U^μ = σU_νF^μν
J^μ - (T_νJ^ν)T^μ = σU_νF^μν
J^μ - V_ν^μJ^ν = σU_νF^μνH_ν^μJ^ν = σU_νF^μν
The covariant generalization of Ohm's Law, where in a rest frame { j = σ e} where (σ) is the conductivity.
Or, a better way to say, Ohm's Law is the spatial component of the above correctly tensorial equation.
When magnetic fields are present, eg. the Hall Effect, then there is an additional term { j = σ(e + u x b) }.
J: SI Units [C/m²·s]
σ: SI Units [S = A²·s³/kg·m³] = [C²·s/kg·m³]
F^μν: SI Units [kg/C·s]
U: SI Units [m/s]
σU_νF^μν: SI Units [C²·s/kg·m³]*[m/s]*[kg/C·s] = [C/m²·s]
The rest charge in a typical conducter is zero as the carriers (electrons) and matrix (nuclei) balance each other.
In SR, the relative motion of the carriers changes this.
This is a strong argument that using currents to produce magnetic fields is a 100% relativistic effect even for relatively slow moving charges.
Start with a rest frame U→U_o = (c,0)
In this rest frame U_oνF^μν = (0,e), so σU_oνF^μν = (0,σ e)
Set J^μ = (cρ,j) = (0,σ e) = σU_oνF^μν
However, since the charge density is known to not be part of Ohm's law, we need to remove it.
One can remove it from the 4-CurrentDensity by finding the temporal component and subtracting,
which is equivalent to taking the Spatial Projection Tensor H_ν^μJ^ν.
Thus, we get in simplified form { H_ν^μJ^ν = σU_νF^μν}
Working out the components gives: j = γσ( (e) + (u⨯b) )
=============================

F^μν = (∂^μA_EM^ν - ∂^νA_EM^μ) = ( A_EM^ν,μ - A_EM^μ,ν )
F^μν =

0	-e^x/c	-e^y/c	-e^z/c
e^x/c	0	-b^z	b^y
e^y/c	b^z	0	-b^x
e^z/c	-b^y	b^x	0

F^μν =

0	-eⁱ/c
+e^j/c	-ε_ijkb^k

F_μν =

0	+eⁱ/c
-e^j/c	-ε_ijkb^k

The Electromagnetic Tensor, also known as the Faraday Tensor, or as the EM Tensor (SI Units = [T] = [kg/A·s²] = [kg/C·s])
can be constructed from the 4-Gradient and 4-EM_VectorPotential 4-Vectors.
F^μν:SI Units [T] = [kg/A·s²] = [kg/C·s]
A: SI Units [kg·m/C·s]
∂: SI Units [1/m]
J : SI Units [C/m²·s]
e: SI Units [kg·m/A·s³] = [kg·m/C·s²]
e/c: SI Units [kg/C·s]
b: SI Units [T] = [kg/A·s²] = [kg/C·s]
ε_o: SI Units [F/m] = [C²·s²/kg·m³]
μ_o: SI Units [H/m] = [kg·m/C²]
Note that the EM Tensor is a 2nd rank, anti-symmetric tensor ( F^μν = -F^νμ), which gives it some really useful properties.
At this point in the presentation, I am simply showing the results of throwing the 4-Gradient at the 4-EM-VectorPotential.
We can see how this is actually derived (in the section on the Lorentz Force Law).

Note that writing out the complete 4x4 matrix using F^μν = (∂^μA_EM^ν - ∂^νA_EM^μ) for each cell gets tedious.
Using slick tensor calculus index gymnastics, let's instead define some meaningful labels for the individual cells:

F^μμ = (∂^μA_EM^μ - ∂^μA_EM^μ) = 0 down the diagonal

F⁰ⁱ = (∂⁰A_EMⁱ - ∂ⁱA_EM⁰) = (∂^t/c aⁱ + ∇ⁱφ/c) = - eⁱ/c
Fⁱ⁰ = (∂ⁱA_EM⁰ - ∂⁰A_EMⁱ) = (-∇ⁱφ/c - ∂^t/c aⁱ) = + eⁱ/c
{F⁰ⁱ = -Fⁱ⁰as expected...}

F^ij = (∂ⁱA_EM^j - ∂^jA_EMⁱ)
= ( δⁱ_lδ^j_m - δ^j_lδⁱ_m)∂^lA_EM^m
= ( ε^kijε_klm)∂^lA_EM^m
= ( ε^ijk)[-∇⨯a]_k
= -( ε^ijk)b_k
= -ε_ijkb^k
{ε_ijk = -ε_jik, giving F^ij = - F^jias expected...}

So, e = (-∇φ - ∂^ta) and b = [∇⨯ a]
or, eⁱ = cFⁱ⁰ and b^k = -(1/2)ε_ij^kF^ij

The overall Lorentz Transform of F^μν requires two separate Lorentz Transform Tensors:
F^μ'ν' = Λ^μ'_αΛ^ν'_β F^αβ

*Note* For many years many textbooks have said that the electromagnetic (e) and (b) fields were the "real" objects of reality, and that the potential (φ) and vector-potential (a) were mathematical artifacts. This is now known to be incorrect. (e) and (b) were discovered during classical Euclidean-space physics, before it was understood that the 4-EM-VectorPotential A_EM was one of the standard SR 4-Vectors in 4D Minkowski SpaceTime.
(e) and (b) are actually derived from the correctly relativistic 4-Gradiant and 4-EM-VectorPotential, which can be combined in a specific way to make the Faraday EM Tensor. In fact, (e) and (b) may be regarded as a convenience, simply a handy label for each of the 16 cells in the EM Faraday Tensor matrix. One can write the manifestly covariant Maxwell and Lorentz Force Equations without any reference to (e) and (b) if desired. However, it turns out that the labels are very useful for writing down the pre-relativistic classical EM equations. The other reason that (e) and (b) are secondary is because once QM comes into play via the Aharonov-Bohm or Aharonov-Casher effects, the 4-EM-VectorPotential A_EM = (φ/c,a) is required to describe the phenomena.

One reason for much of the confusion is that there seems to be a discrepancy over the number of degrees of freedom via each choice.
The 4-EM-Potential and the 4-Gradient have 4 independent components each, for a total of 8 degrees of freedom.
The (e) and (b) fields have 3 independent components each, for a total of 6 degrees of freedom.
Which is correct? Scalar Lorentz invariants come to the rescue.

There are some Lorentz Invariants associated with any rank-2 tensor T^μν.
These principle invariants are defined by eigenvalues (λ_i) of T.

Invariant #1: The Trace: Tr[T^μν] = η_μνT^μν = T_μ^μ = T_ν^ν
Tr[F^μν] = F_ν^ν = F₀⁰ + F₁¹ + F₂² + F₃³ = 0 + 0 + 0 + 0 = 0
Hence: Tr[F^μν] = 0

Invariant #2: Half The Inner Product: (1/2)T^μνT_μν = (1/2) T^μνη_μαη_νβT^αβ = (1/2){Tr[T]² -Tr[T²]}
*** Note - It may actually be half the outer product, not sure, I may have benefitted from the Antisymmetry ***
F^μνF_μν =
F⁰⁰F₀₀ + F⁰ⁱF_0i + Fⁱ⁰F_i0 + F^ijF_ij
(0*0) + (- eⁱ/c)(- e_i/c) + ( + eⁱ/c)( + e_i/c) + (-ε_ijkb^k)(-ε^ijkb_k)
(0*0) + (- eⁱ/c)(- - eⁱ/c) + ( + eⁱ/c)(- + eⁱ/c) + (-ε_ijkb^k)(- - -ε_ijkb^k)
(0) + (- eⁱ/c)( + eⁱ/c) + ( + eⁱ/c)(- + eⁱ/c) + (ε_ijkε_ijkb^k* b^k)
(0) + -(e/c)² + -(e/c)² + (ε_ijε_ij)(b)²
(0) + -(2)(e/c)² + (2)(b)²
2{b² -(e/c)²}
F^μνF_μν = 2{ b·b - e·e/c²}

Hence: (1/2)F^μνF_μν = {b·b - e·e/c²} = {b·b - e·e*(ε_oμ_o)}
*Note* (1/4μ_o)F^μνF_μν = (1/2){ b·b/μ_o - ε_oe·e}
u_e = the EM energy density = (1/2){ b·b/μ_o + ε_oe·e} = (1/2){ε_oe·e + b·b/μ_o}
They differ by a minus sign

Invariant #3: The Determinant: Det[T^μν] = ??? = ε_μνρσT^μ0T^ν1T^ρ2T^σ3
Ok, this is gonna be ugly... or maybe not... thank you skew-symmetric, dimension 4...
The determinant of a (2n) x (2n) skew-symmetric matrix can always be written as the square of a polynomial in the matrix entries.
This polynomial is called the Pfaffian.
Det[F^μν] = Pfaffian[F^μν]²
Pf[[0, a, b, c]
[-a, 0, d, e]
[-b,-d,0, f]
[-c,-e,-f, 0]] = af-be + cd
Pfaffian[F^μν] = (-e^x/c)(-b^x) - (-e^y/c)(b^y) + (-e^z/c)(-b^z) = (e^xb^x/c) + (e^yb^y/c) + (e^zb^z/c) = (e·b)/c
Det[F^μν] = {(e·b)/c}²

{#1} doesn't really do anything for us, since 0 = 0 doesn't place any constraints.
But, {#2} and {#3} provide 2 constraints on the total degrees of freedom.

There were originally 4 + 4 = 8 degrees of freedom from (4-Gradient + 4-VectorPotential), but now there are only 6 due to the 2 constraints.
This matches the total of 6 independent components from the (e) and (b) fields.
This seems correct, since I can think of situations/experiments for which I can set the (e) and (b) fields to whatever I want, and vary each of the components individually to get independent results.
Looking at it a different way:
A 4x4 matrix can have up to 16 independent components.
But, we can always break a tensor into a sum of a symmetric and anti-symmetric tensor.
T^μν = (T^μν + T^νμ)/2 {symmetric} + (T^μν - T^νμ)/2 {anti-symmetric}
For the 4x4 = 16 case, this breaks down into symmetric (at most 10 independent components) + anti-symmetric (at most 6 independent components)
The fact that the Faraday Tensor is 4x4 anti-symmetric (or skew-symmetric) again takes the total of independent components down to 6.

There are a few situations for these invariant conditions:
If {(e·b)/c}=0 and {b·b - e·e/c²}=0, then this describes a "null EM field", with the e and b fields perpendicular to each other and of fixed "equivalent unit" {|e|/c = |b|}magnitude.
This would represent an EM plane-wave in Minkowski SpaceTime.

If {(e·b)/c}=0 but {b·b - e·e/c²}≠0, then this describes a "non-null EM field", with an inertial frame for which either the e or b field vanishes: magnetostatic (|e|=0) or electrostatic (|b|=0) fields.

If {(e·b)/c}≠0 then there is an inertial frame in which the e and b fields are proportional.
=============================

Tr[F^μν] = η_μνF^μν = η_μν(∂^μA_EM^ν - ∂^νA_EM^μ) = η_μν∂^μA_EM^ν - η_μν ∂^νA_EM^μ = ∂_νA_EM^ν - ∂_μA_EM^μ = 0
The Trace of the anti-symmetric Faraday tensor is zero.
Actually, the Trace of any anti-symmetric tensor is zero.
Tr[F^μν] = η_μνF^μν = F_ν^ν
but [F_ν^ν] = -[F_ν^ν] = 0 for all ν for an anti-symmetric tensor
so Tr( F^μν) = 0
Alternately, constructing an antisymmetric (2,0)-tensor
C^μν = ( A^μB^ν - A^νB^μ)
Tr[C^μν] = η_μνC^μν = η_μν( A^μB^ν - A^νB^μ) = η_μν( A^μB^ν) - η_μν( A^νB^μ) = ( A_νB^ν) - ( A_μB^μ) = 0
=============================

Faraday Electromagnetic Tensor

Magnetization-Polarization Tensor

Electromagnetic Displacement Tensor

F^αβ = (∂^αA_EM^β - ∂^βA_EM^α)

F^αβ =

0	-e^x/c	-e^y/c	-e^z/c
e^x/c	0	-b^z	b^y
e^y/c	b^z	0	-b^x
e^z/c	-b^y	b^x	0

F^μν =

0	-eⁱ/c
+e^j/c	-ε^ij_kb^k

M^αβ =

0	p^xc	p^yc	p^zc
-p^xc	0	-m^z	m^y
-p^yc	m^z	0	-m^x
-p^zc	-m^y	m^x	0

0	+pⁱc
-p^jc	-ε^ij_km^k

D^αβ =

0	-d^xc	-d^yc	-d^zc
d^xc	0	-h^z	h^y
d^yc	h^z	0	-h^x
d^zc	-h^y	h^x	0

0	-dⁱc
+d^jc	-ε^ij_kh^k

e = eⁱ = electric field
b = b^k = magnetic field

p = pⁱ = electric polarization (polarization)
m = m^k = magnetic polarization (magnetization)

d = dⁱ = electric displacement field
h = h^k = auxiliary magnetic field

F^αβ:SI Units [T] = [kg/A·s²] = [kg/C·s]
e: SI Units [kg·m/A·s³] = [kg·m/C·s²]
e/c: SI Units [kg/C·s]
b: SI Units [T] = [kg/A·s²] = [kg/C·s]

M^αβ: SI Units [C/m·s]
p: SI Units [C/m²]
pc: SI Units [C/m·s]
m: SI Units [C/m·s]

D^αβ: SI Units [C/m·s]
d: SI Units [C/m²]
dc: SI Units [C/m·s]
h: SI Units [C/m·s]

∂_β F^αβ = μ_o J^α

∂_β M^αβ = J_bound^α

∂_β D^αβ = J_free^α

A: SI Units [kg·m/C·s]
∂: SI Units [1/m]
J,J_free,J_bound : SI Units [C/m²·s]
ε_o: SI Units [F/m] = [C²·s²/kg·m³]
μ_o: SI Units [H/m] = [kg·m/C²]

The EM Tensors can be decomposed in the free and bound parts.
These are all anti-symmetric.

D^αβ = (1/μ_o)F^αβ - M^αβ

Time-Space Components	Purely Spatial Components
(-dc) = (1/μ_o)(-e/c) - (pc) (-dc) = (c²ε_o)(-e/c) - (pc) (-dc) = (ε_o)(-ec) - (pc) (-d) = (ε_o)(-e) - (p) (d) = (ε_o)(e) + (p) d = ε_oe + p	(h) = (1/μ_o)(b) - (m) h = (1/μ_o)b - m b = μ_o(h + m)

F^αβ = μ_o(D^αβ + M^αβ)
∂_β F^αβ = ∂_β μ_o(D^αβ + M^αβ)
∂_β F^αβ = μ_o(∂_β D^αβ + ∂_β M^αβ)
μ_o J^α = μ_o(J_free^α+ J_bound^α)
J^α = J_free^α+ J_bound^α

Each of these is individually conserved due to the anti-symmetric tensor they are formed from.

In physics, the electric displacement field, denoted by D, is a vector field that appears in Maxwell's equations. It accounts for the effects of free and bound charge within materials while its sources are the free charges only. "D" stands for "displacement", as in the related concept of displacement current in dielectrics. In free space, the electric displacement field is equivalent to flux density, a concept that lends understanding to Gauss's law.

In classical electromagnetism, polarization density (or electric polarization, or simply polarization) is the vector field that expresses the density of permanent or induced electric dipole moments in a dielectric material. When a dielectric is placed in an external electric field, its molecules gain electric dipole moment and the dielectric is said to be polarized. The electric dipole moment induced per unit volume of the dielectric material is called the electric polarization of the dielectric.
In classical electromagnetism, magnetization or magnetic polarization is the vector field that expresses the density of permanent or induced magnetic dipole moments in a magnetic material. The origin of the magnetic moments responsible for magnetization can be either microscopic electric currents resulting from the motion of electrons in atoms, or the spin of the electrons or the nuclei.

see Constitutive Equation, Covariant Formulation of Classical EM, 4-Tensor, Maxwell's equations in curved SpaceTime,

∂_α J^α = ∂_α ∂_β D^αβ = 0 due to anti-symmetry (conservation of 4-CurrentDensity)
see
L_den = -(1/4μ_o)F^μνF_μν - A·J_free for EM field
L_den = L_den(field) + L_{den(interaction)} for EM field

L_den = -(1/4μ_o)F^μνF_μν - A·J_free + (1/2)F_αβM^αβ with free and bound currents separated
L_den = -(1/4μ_o)2{b·b - e·e/c²} - {(φ/c)(ρ_freec) - a·j_free} - (1/2){2(e·p + b·m)} with free and bound currents separated
L_den = -(1/2μ_o){b·b - e·e/c²} - {(φ)(ρ_free) - a·j_free} + {(e·p + b·m)}
L_den = (1/2μ_o){- b·b + e·e/c²} - (φ)(ρ_free) + a·j_free + (e·p + b·m)
L_den = (1/2){- b·b/μ_o + ε_oe·e/c²} - (φ)(ρ_free) + a·j_free + (e·p + b·m)
L_den = (1/2){ε_oe·e/c² - b·b/μ_o} -φρ_free + a·j_free + e·p + b·m

F_αβM^αβ
= F_ttM^tt + F_tsM^ts + F_stM^st + F_ssM^ss
=(0) + -(e·p) + -(e·p) + 2(b·m)
=2{-(e·p) + (b·m)}???
=============================

σ^μν
=

0	d^x/c	d^y/c	d^z/c
-d^x/c	0	-μ^z/c	μ^y/c
-d^y/c	μ^z/c	0	-μ^x/c
-d^z/c	-μ^y/c	μ^x/c	0

0	+dⁱ/c
-d^j/c	-ε^ij_kμ^k

The Electromagnetic Dipole Tensor of a single particle
It is anti-symmetric.
The d = dⁱ components are the electric dipole moments and the μ = μⁱ components are the magnetic dipole moments.

see 4-Tensor,

=============================

M^μν = (X^μP^ν - X^νP^μ) = X^μ ^ P^ν =

[ 0 ,-n^xc,-n^yc,-n^zc]
[n^xc, 0 , L^z , -L^y ]
[n^yc, -L^z, 0, L^x ]
[n^zc, L^y, -L^x, 0] =

[     0 , -nⁱc ]
[+ n^jc, ε^ij_kL^k] =

[     0 , - nc ]
[+ n^Tc, x ^ p]
The relativistic angular momentum tensor, which is an anti-symmetric tensor in exactly the same way as the Faraday EM Tensor.
n is a relativistic mass moment.
L is the standard 3D angular momentum

If M^μν is for a free particle (no interactions), then d/dτ[P^μ] = 0, which means P^μ = const.
Then
d/dτ[M^μν] =
= d/dτ[(X^μP^ν - X^νP^μ)]
= d/dτ[X^μP^ν] - d/dτ[X^νP^μ]
= d/dτ[X^μ] P^ν + X^μd/dτ[P^ν] - d/dτ[X^ν] P^μ - X^νd/dτ[ P^μ]
= d/dτ[X^μ] P^ν + (0) - d/dτ[X^ν] P^μ - (0)
= U^μP^ν - U^νP^μ
= m_o(U^μU^ν - U^νU^μ)
= 0

The Fokker-Synge Equation also gives { U_μM^μν = 0 }, a Lorentz Invariant expression that the Relativistic Angular Momentum is orthogonal to the worldline.
This is just like the Lorentz Invariant condition for Photon Polarization { Ε·K = (ε⁰,ε)·(ω/c)(1,β) = (ω/c)(ε⁰*1 - ε·β) = 0 }

The 4-TotalAngularMomentumTensor J^μν = M^μν + S^μν , with S^μν as the intrinsic (point) 4-AngularMomentum or 4-SpinTensor.
This is the Spin-Orbital Decomposition, and applies to particles, mass-energy-momentum distributions, or fields.

see Relativistic Angular Momentum
=============================

∂_νM^μν = Z = (0,0) {if conservative} (Conservation of Centroid and Angular Momentum)
=============================

Relativistic Torque (4-Couple) Tensor G^μν = (X^μF^ν - X^νF^μ) = X^μ ^ F^ν = d/dτ[M^μν]
=
[    0 , -?c ]
[+?^Tc, x ^ f]
The relativistic 4-Couple tensor, which is an anti-symmetric tensor in exactly the same way as the Faraday EM Tensor.
=============================

U·F_EM = U_μF_EM^μ = U_μ( qU_νF^μν) = qU_μU_υ(∂^μA_EM^ν - ∂^νA_EM^μ) = 0
Beautiful result showing the the EM field is a conservative field (a pure 4-Force).
The contraction of the two 4-Velocities (symmetric) with the EM-Tensor (anti-symmetric) guarantees a zero result.
Hence, the 4-EM-Force is always spatial, and orthogonal to the timelike 4-Velocity.
Proof:
F^μν = -F^νμ: Def. of Anti-Symmetric Tensor
Let V_μ be a generic index-lowered 4-Vector
(F^μν)(V_μ)(V_ν) = (F^νμ)(V_ν)(V_μ): switching dummy indices
(-F^μν)(V_ν)(V_μ): anti-symmetry
(-F^μν)(V_μ)(V_ν): commuting 4-Vectors
Hence: (F^μν)(V_μ)(V_ν) = -(F^μν)(V_μ)(V_ν) = 0
This can also be viewed as another Invariant Rest Temporal Component Rule.
Essentially, the Temporal component does not change in time.
=============================

∂_α(∂^αA_EM^ν - ∂^νA_EM^α) = ∂_αF^αν = μ_oJ^ν
(∂·∂)A_EM - ∂(∂·A_EM) = μ_oJ
∂·F^αν = μ_oJ
∂^αF^μν + ∂^νF^αμ + ∂^μF^να = F^[αμ,ν] = 0^αμν
The full Non-Homogeneous Classical Maxwell EM Equation (any gauge).
It can be written in a few different informative ways.
The 1st is in single index Tensor format.
The 2nd is in 4-Vector format.
The 3rd is a slightly ambiguous mix of 4-Vector and 2 index Tensor that emphasizes the fact that the Maxwell EM equation is actually just another type of 4-Divergence equation.
The 4-CurrentDensity is the source/sink of the Electromagnetic Tensor.
Also we have:
∂^αF^μν + ∂^νF^αμ + ∂^μF^να = F^[αμ,ν] = 0^αμν
which is a Tensor form of the Bianchi/Jacobi Identity.
∂^α F^μν + ∂^ν F^αμ + ∂^μ F^να =
∂^α(∂^μA^ν - ∂^νA^μ) + ∂^ν(∂^αA^μ - ∂^μA^α) + ∂^μ(∂^νA^α - ∂^αA^ν) =
∂^α∂^μA^ν - ∂^α∂^νA^μ + ∂^ν∂^αA^μ - ∂^ν∂^μA^α + ∂^μ∂^νA^α - ∂^μ∂^αA^ν =
rearrange terms...
+ ∂^μ∂^νA^α - ∂^ν∂^μA^α + ∂^ν∂^αA^μ - ∂^α∂^νA^μ + ∂^α∂^μA^ν - ∂^μ∂^αA^ν =
partials commute...
+ ( ∂^μ∂^νA^α - ∂^μ∂^νA^α) + (∂^α∂^νA^μ - ∂^α∂^νA^μ) + ( ∂^α∂^μA^ν - ∂^α∂^μA^ν) =
(0) + (0) + (0) =
0
Can also write these as:
∂_αF^αν = μ_oJ^ν : { Gauss –Ampère law (vacuum)}
∂_α(1/2)( ε^αβγδF_γδ) = 0^β : {Gauss–Faraday law (vacuum)}
=============================

∂_ν∂_α(∂^αA_EM^ν - ∂^νA_EM^α) = ∂_ν∂_αF^αν = μ_o∂_νJ^ν = 0
(∂·J) = 0 {for an EM field}
The conservation of charge, or continuity equation for the 4-CurrentDensity of an EM field.
Another beautiful result showing the power of tensors.
The contraction of the two 4-Gradients (symmetric) with the EM-Tensor (anti-symmetric) guarantees a zero result.
Proof:
F^μν = -F^νμ: Def. of Anti-Symmetric Tensor
Let V_μ be a generic index-lowered 4-Vector
(F^μν)(V_μ)(V_ν) = (F^νμ)(V_ν)(V_μ): switching dummy indices
(-F^μν)(V_ν)(V_μ): anti-symmetry
(-F^μν)(V_μ)(V_ν): commuting 4-Vectors
Hence: (F^μν)(V_μ)(V_ν) = -(F^μν)(V_μ)(V_ν) = 0
=============================

∂·A_EM = (∂_t/c,-∇)·(φ/c,a) = (∂_tφ/c² + ∇·a) = 0 {Lorenz Gauge}
∂·A_EM = 0 → K·E = 0
The Lorenz Gauge for Classical EM - Yes, Lorenz, not Lorentz :)
It simplifies the expression for the Maxwell EM Equations.
Again, it is showing that the 4-Divergence is zero and hence the EM field is conservative, no sources or sinks.
From pure math: ∂·[φV] = ∂[φ]·V + φ(∂·V), with (φ) a Lorentz scalar and (V) a 4-Vector.
A_EM = a Ε e^(-i K·X) = a Ε e^(-iΦ), The 4-EM-VectorPotential has plane wave solutions.
∂·[A_EM] = 0 = ∂·[a Ε e^(-iΦ)] = a ∂[e^(-iΦ)]·Ε + a e^(-iΦ)(∂·Ε) = a i K·Ε e^(-iΦ) + (0) = 0
Hence, K·Ε = 0, the 4-Polarization is orthogonal to the 4-WaveVector.
=============================

(∂·∂)A_EM = μ_oJ{for ∂·A_EM = 0 : Lorenz Gauge, if the EM field is conservative}
The "reduced" Non-Homogeneous Classical Maxwell EM Equation, considering a conservative field, and not considering particle spin.
(∂·∂)(φ/c,a) = (∂_t²/c² - ∇·∇)(φ/c,a) = μ_o(cρ,j)
Temporal Component: (∂·∂)[φ] = μ_o(c²ρ) = ρ/ε_o
Spatial Component: (∂·∂)[a] = μ_oj
with { ε_oμ_o = 1/c² }
(∂·∂)(A_EM·U) = μ_o(J·U)
(∂·∂)φ_o = μ_oρ_oc²
(∂·∂)φ_o = ρ_o/ε_o
This is from classical EM, which was actually the starting point for Einstein's theories of Relativity.
Let's examine the 4-VectorPotential of a point charge
φ = (γΦ_o) = (γq/4πε_o)/r
(∂·∂)φ
= (∂·∂) (γq/4πε_o)[1/r]
= (γq/4πε_o)(∂·∂)[1/r]
= (γq/4πε_o)4πδ³(r)
= (γq/ε_o)δ³(r)
= (γq)δ³(r)/ε_o
= ρ/ε_o
with ρ = (γq)δ³(r) and thus ρ_o = (q)δ³(r)

(∂·∂)A_EM = μ_oJ
A_EM = (μ_o/4π) ∫dτ J/τ

Just a note: The classical Maxwell EM equations do not have Spin included
(∂·∂)A_EM = μ_oJ = μ_oρ_oU = μ_o(q/V_o)U = μ_oq(c/V_o)T
Once spin is included, the equations for QED emerge:
(∂·∂)A_EM = μ_oqψ Γψ
with the 4-CurrentDensity J = qψ Γψ, 4-DiracGammaMatrix Γ = (γ⁰,γ)

Finally, just an interesting EM comparison, we can get the Maxwell and Lorentz Force Equations in almost identical format:

Maxwell Eqn	∂_α(∂^αA_EM^ν - ∂^νA_EM^α) = μ_oJ^ν	∂·F^αν = (μ_o)J	Divergence of Faraday EM Tensor
Lorentz Force Eqn	U_α(∂^νA_EM^α - ∂^αA_EM^ν) = (1/q)F^ν	U·F^αν = (-1/q)F	Invariant Temporal Component of Faraday EM Tensor

The two physical constants obtained from ElectroMagnetic SR are (q) and (μ_o).
(ε_o) is not an independent constant; it is related via (ε_o)(μ_o) = 1/c²
=============================

Ε*·Ε = (ε⁰,ε)*·(ε⁰,ε) = (ε⁰)² - ε*·ε → -1
The 4-Polarization (which may be complex valued, hint hint) has a spatial magnitude of -1.
The 4-Polarization has vertical and horizonal polarizations, and is known to have complex components, which give rise to left/right circular and elliptical polarizations.
=============================

Ε·K = (ε⁰,ε)·(ω/c)(1,β) = (ω/c)(ε⁰*1 - ε·β) = 0
The 4-Polarization is orthogonal to the 4-WaveVector.
From pure math: ∂·[φ V] = ∂[φ]·V + φ(∂·V), with φ a Lorentz scalar and V a 4-Vector
A_EM = aΕe^{(-i K·X)} = aΕe^(-iΦ), the 4-EMVectorPotential has plane wave solutions.
If we choose the Lorenz Gauge, which is appropriate for a conservative field:
∂·[A_EM] = 0 = ∂·[aΕe^(-iΦ)] = a∂[e^(-iΦ)]·Ε + ae^(-iΦ)(∂·Ε) = aiK·Εe^(-iΦ) + (0) = 0
Hence, K·Ε = 0, the 4-Polarization is orthogonal to the 4-WaveVector.
=============================

S = S_act = -(P_T·R) or S = -(P_T·X) and ∂[S] = -P_T
S = S_act = -∫(P_T·dR) = -∫(P_T·U)dτ = -∫(P_T·U/γ)dt = ∫L dt
Getting into Relativistic Analytic Mechanics, we can define a Lorentz Invariant Action (S = S_act) as the negative Lorentz Scalar product of the 4-TotalMomentum with the 4-Position,
or the 4-TotalMomentum is the negative 4-Gradient of the Action. If the worldline is curved then the integral form with the Lagrangian can be used.
(L dt) is also a Lorentz Invariant.
This leads to the Relativistic Hamilton-Jacobi Equation.
P_T = (H/c,p_T) = -∂[S] = (-∂_t[S]/c,∇[S])
giving:
temporal component H = -∂_t[S]
spatial component p_T = ∇[S]

Using some results from before:
P_T = P + qA_EM
P·P = (E/c)² - p·p = (m_oc)²
P = (E/c,p) = P_T - qA_EM = -∂[S] - qA_EM = (-∂_t[S]/c - qφ/c,∇[S] - qa)
And putting it all together...
(-∂[S] - qA_EM)·(-∂[S] - qA_EM) = (m_oc)²
(-∂_t[S]/c - qφ/c)² - (∇[S] - qa)·(∇[S] - qa) = (m_oc)²
(∂_t[S]/c + qφ/c)² - (∇[S] - qa)² = (m_oc)²
This is the Relativistic Hamilton-Jacobi Equation including the effects of a 4-VectorPotential.

We can also define:
Relativistic Hamiltonian H = γ(P_T·U)
Relativistic Lagrangian L = -(P_T·U)/γ
with H + L = p_T·u
This comes from the relativistic identity:
γ -1/γ = γβ²
Just multiply all the terms by the Lorentz Scalar (P_T·U)
γ(P_T·U) + -(P_T·U)/γ = γ(P_T·U)β²

Hamiltonian	Lagrangian	Combo
H	L	H + L = p_T·u
γ(P_T·U)	-(P_T·U)/γ	γ(P_T·U)β²
γH_o	L_o/γ	γH_o + L_o/γ

Rest Hamiltonian	Rest Lagrangian	Rest Combo = 0
H_o	L_o	H_o + L_o = 0 = p_T·0
(P_T·U)	-(P_T·U)	(1)(P_T·U)(0)² = 0
H/γ	γL	0

The Relativistic Lorentz Invariant Action
S = -∫(P_T·dR) = -∫(P_T·U)dτ = -∫(P_T·U/γ)dt = ∫L dt
see Action(physics)

Example of a free relativistic point particle:
P_T → P = (E/c,p) = (mc,p): For a free particle the 4-TotalMomentum is just the 4-Momentum of the particle
P_T·U → P·U = (mc,p)·γ(c,u) = γ(mc² - p·u) = m_oc²
L = - (P_T·U)/γ → - (m_oc²)/γ
S = -∫(P_T·dR) = -∫(P_T·U)dτ = -∫(P_T·U/γ) dt = ∫L dt → - (m_oc²)∫(1/γ)dt = - (m_oc²)∫dτ
H = γ(P_T·U) → γ(m_oc²) = (mc²) = E
T = (γ-1)(P_T·U) → (γ-1)(m_oc²) = (mc²) - (m_oc²) = E - E_o : The Relativistic Kinetic Energy

Example of a relativistic point particle minimally coupled to an EM field:
P_T → P + Q = P + qA = (E/c + qφ/c,p + qa):
P_T·U → (P + qA)·U = (P·U + qA·U ) = (mc,p)·γ(c,u) + q(φ/c,a)·γ(c,u) = γ(mc² - p·u) + γq(φ - a·u) = m_oc² + qφ_o
L = - (P_T·U)/γ → - (m_oc² + qφ_o)/γ = - (m_oc² + γq(φ - a·u))/γ = - (m_oc²)/γ - q(φ - a·u)
S = -∫(P_T·dR) = -∫(P_T·U)dτ = -∫(P_T·U/γ) dt = ∫L dt → - (m_oc² + qφ_o)∫(1/γ)dt = - (m_oc² + qφ_o)∫dτ
H = γ(P_T·U) → γ(m_oc² + qφ_o) = (mc² + qφ) = E_T
T = ?? : The Relativistic Kinetic Energy - Not sure if only to subtract the rest mass of just the particle or also the rest scalar field

*Note*
The Action S, the Rest Energy E_o: are Lorentz Invariant Scalars (as they can be written as the scalar product of 4-Vectors).
The Hamiltonian H, the Lagrangian L, the Kinetic Energy T: are NOT Lorentz Invariant Scalars (they have factors of γ in them).
However, H_o = (H/γ) = (P_T·U) and L_o = (γL) = -(P_T·U) are Lorentz Invariant, with H_o = -L_o
=============================

L_den = -n_o(P_T·U) = (n_o)(-P_T·U) = (n/γ)(γL) = nL = n_oL_o
L_den = -n_o(P_T·U) = -(n_o)(E_To) = -u_eTo
The Lagrangian Density is a Lorentz Scalar Invariant.
The regular Lagrangian L = -(P_T·U)/γ
However, try (nL), where n = Relativistic NumberDensity, with n = γn_o
Then (nL) = -n(P_T·U)/γ = -(γn_o)(P_T·U)/γ = -(n_o)(P_T·U)
L_den = -n_o(P_T·U)
= -n_o((P + qA)·U)
= -n_o((P + qA)·U)
= -n_o(P·U + qA·U)
= -(n_oP·U + n_oqA·U)
= -(n_oP·U + ρ_oA·U)
= -(G·U + A·J), where G is a 4-MomentumDensity
= -(E_deno + A·J)
= -(u_eo + A·J),
Have to stop here: Can't be used for EM since there is no rest-frame for photonic

(1/4μ_o)F^μνF_μν = (1/4μ_o)(2{ b·b - e·e/c²})= -(1/2){ε_oe·e - b·b/μ_o} = u_eo = the "rest" EM energy density
(-1/4μ_o)F^μνF_μν = (-1/4μ_o)(2{ b·b - e·e/c²})= (1/2){ε_oe·e - b·b/μ_o}
(1/2){ε_oe·e + b·b/μ_o} = u_eo = the "rest" EM energy density
They differ by a sign

L_den(field) + L_{den(interaction)} = L_den for EM field
see Covariant formulation of classical EM

<< need to move this section >>
Try with the Dirac Equation...
iћΨ̅ (Γ^μ∂_μ)Ψ = Ψ̅(m_oc)Ψ
Ψ̅ iћ(Γ^μ∂_μ) - (m_oc)Ψ = 0
Ψ̅ iћc(Γ^μ∂_μ) - (m_oc²)Ψ = 0 to get all terms in units of [Energy]

Let the 4-TotalMomentum = 4-Zero, then the TotalRestEnergyDensity = 0 {Just a convenient reference point}
L_den = -n_o(P_T·U)
L_den = Ψ̅ iћc(Γ^μ∂_μ) - (m_oc²)Ψ = Ψ̅ iћc(Γ^μ∂_μ)Ψ - (m_oc²)Ψ̅ Ψ = The Dirac Lagrangian
where the number density is carried by the Ψ̅ Ψ

For an electron in an EM field, the 4-TotalMomentum would include the term for the EM field
L_den = -n_o(P_T·U)
L_den = Ψ̅ iћc(Γ^μ∂_μ) - (m_oc²) Ψ - (1/4μ_o)F^μνF_μν = Ψ̅ iћc(Γ^μ∂_μ)Ψ - (m_oc²)Ψ̅ Ψ - (1/4μ_o)F^μνF_μν = The QED Lagrangian
see Lagrangian (Field Theory)
=============================

d⁴X = -(V_o)dT·dX = cdt d³x = cdt dx dy dz
The 4D Position coords that are integrated to give a 4D volume: SI Units [m⁴]
4-Differential dX = (cdt,dx); dR = (cdt,dr);
4-UnitTemporal T = γ(1,β) = (γ,γβ)
4-UnitTemporalDifferential dT = d[(γ,γβ)] = (d[γ],d[γβ])

V = ∫dV = ∫dx ∫dy ∫dz = ∫∫∫dx dy dz = ∫d³x
V = V_o/γ = 3D Spatial Volume: SI units [m³]
dV = ∫d³x = 3D Spatial Volume Element
γ = V_o/V
dγ = -(V_o/V²)dV

-(V_o)dT·dX = Invariant, because (Rest Scalar * Lorentz Scalar Product) = Invariant
= -(V_o)(d[γ],d[γβ])·(cdt,dx)
= -(V_o)(d[γ]cdt - d[γβ]·dx)
= -(V_o)(-(V_o/V²)dVcdt - d[γβ]·dx)
= -(V_o)(-(V_o/V_o²)dVcdt - d[(1)(0)]·dx) by taking the usual rest-case
= -(V_o)(-(V_o/V_o²)dVcdt)
= -(V_o)(-(1/V_o)dVcdt)
= dVcdt
= cdt dV
= cdt dx dy dz
= cdt d³x
= d⁴X = Invariant
And, this makes sense.
T is a temporal 4-Vector with fixed magnitude: T·T = 1
Therefore, dT must be a spatial 4-Vector
If dX is also spatial, then the Lorentz scalar product { (dT·dX) = -magnitude } will be negative with this choice of Minkoski Metric.
Thus, multiplying by -(V_o) gives a positive volume element{ cdt dx dy dz = d⁴X}
It is sort of quirky though, that the temporal (cdt) comes from the dR part, and the spatial (d³x) comes from the dT part.
=============================

d⁴P = (V_Po)dT·dP = (dE/c) d³p = (dE/c) dp^xdp^ydp^z
d⁴K = (V_Ko)dT·dK = (dω/c) d³k = (dω/c) dk^xdk^ydk^z
The 4D Momentum coords that are integrated to give a 4D Momentum Volume: SI Units [(kg·m/s)⁴]
The 4D WaveVector coords that are integrated to give a 4D WaveVector Volume: SI Units [(1/m)⁴]
4-DifferentialMomentum dP = (dE/c,dp)
4-DifferentialWaveVector dK = (dω/c,dk)
4-UnitTemporal T = γ(1,β) = (γ,γβ)
4-UnitTemporalDifferential dT = d(γ,γβ) = (d[γ],d[γβ])

V_P = ∫dV_p = ∫dp^x∫dp^y∫dp^z = ∫∫∫dp^x dp^y dp^z = ∫d³p
V_P = γV_Po = 3D Volume in Momentum Space: SI Units [(kg·m/s)³]
dV_P = dγV_Po = 3D Volume Element in Momentum Space
γ = V_P/VPo
dγ = dV_P/V_Po

(V_Po)dT·dP = Invariant, because (Rest Scalar * Lorentz Scalar Product) = Invariant
= (V_Po)(d[γ],d[γβ])·(dE/c,dp)
= (V_Po)(d[γ]dE/c - d[γβ]·dp)
= (V_Po)((dV_P/V_Po)dE/c - d[γβ]·dp)
= (V_Po)((dV_P/V_Po)dE/c - d[(1)(0)]·dp) by taking the usual rest-case
= (V_Po)((dV_P/V_Po)dE/c)
= (dV_P) (dE/c)
= d³p(dE/c)
= (dE/c) d³p
= (dE/c) dp_xdp_ydp_z
= d⁴P = Invariant
=============================

d³p d³x = (V_Po)dT·(-V_o)dT = (-V_oV_Po)dT·dT
d³k d³x = (V_Ko)dT·(-V_o)dT = (-V_oV_Ko)dT·dT
4-UnitTemporal T = γ(1,β) = (γ,γβ)
4-UnitTemporalDifferential dT = d[(γ,γβ)] = (d[γ],d[γβ])
(V_Po)dT·(-V_o)dT
= (V_Po)(d[γ],d[γ β])·(-V_o)(d[γ],d[γβ])
= (V_Po)(-V_o)(d[γ]d[γ] - d[γβ]·d[γβ])
= (V_Po)(-V_o)(-(V_o/V²)dV(dV_P/V_Po) - d[γβ]·d[γβ])
= (V_Po)(-V_o)(-(V_o/V_o²)dV(dV_P/V_Po) - d[(1)0]·d[(1)0])
= (V_Po)(-V_o)(-(V_o/V_o²)dV(dV_P/V_Po))
= (V_Po)dV(dV_P/V_Po))
= dV dV_P
= dV_P dV
= d³p d³x = Invariant
=============================

ρ d³x = ρ' d³x' = (V_o/c)dT·J = Lorentz Scalar Invariant
4-CurrentDensity J = (ρc,j)
4-UnitTemporal T = γ(1,β) = (γ,γβ)
4-UnitTemporalDifferential dT = d[(γ,γβ)] = (d[γ],d[γβ])
V = V_o/γ
dγ = -(V_o/V²)dV
(-V_o/c)dT·J = Invariant, because (Rest Scalar * Lorentz Scalar Product) = Invariant
= (-V_o/c)(d[γ],d[γβ])·(ρc,j)
= (-V_o/c)(d[γ]ρc - d[γβ]·j)
= (-V_o/c)(-(V_o/V²)(dV)(ρc) - d[γβ]·j)
= (-V_o/c)(-(V_o/V_o²)(dV)(ρc) - d[(1)0]·j)
= (-V_o/c)(-(V_o/V_o²)(dV)(ρc))
= (dV/c)(ρc)
= (ρc)(dV/c)
= (ρ)(dV)
= ρ d³x
And since, q = ∫ρ d³x
The Total Charge (q) is likewise a Lorentz Scalar Invariant
=============================

∫_Ω d⁴X (∂·V) = ∮_∂Ω dS (V·N)
The 4D Gauss' Theorem /Stokes' Theorem /Divergence Theorem
Gauss' Theorem in SR is
∫_Ωd⁴X ∂_μV^μ = ∮_∂ΩdS V^μN_μ
∫_Ωd⁴X (∂·V) = ∮_∂ΩdS (V·N)
where:
Ω is a 4D simply-connected region of Minkowski SpaceTime
∂Ω = S is its 3D boundary with its own 3D Volume element dS and outward-pointing 4-UnitHyperSurfaceNormal N.
d⁴X is a 4D Infintesimal Volume Element
V is a an arbitrary 4-Vector
=============================

φ[X] = 1/(2π)⁴∫d⁴K φ̃[K] e^-i(K·X)
The Covariant 4D version of the Fourier Transform.
φ[X] = 1/(2π)⁴∫d⁴K φ̃[K] e^-i(K·X) = ∫d⁴K /(2π)⁴φ̃[K] e^-i(K·X) = ∫dω/[c(2π)] ∫d³k /(2π)³φ̃[ω/c,k] e^{-i(k·x - ωt)}The Inverse Fourier Transform would be:
φ̃[K] = ∫d⁴X φ[X] e^+i(K·X) = ∫d⁴X φ[X] e^+i(K·X) = ∫cdt ∫d³x φ[ct,x]e^{+i(k·x - ωt)}

There is a more symmetrical version available as well, where the normalization factors are set to match each other.
φ[X] = (2π)^-2∫d⁴K φ̃[K] e^-i(K·X) = ∫d⁴K (2π)^-2φ̃[K] e^-i(K·X) = ∫(dω/c)(2π)^-1/2∫d³k (2π)^-3/2φ̃[ω/c,k] e^{-i(k·x - ωt)}The Inverse Fourier Transform would be:
φ̃[K] = (2π)^-2∫d⁴X φ[X] e^+i(K·X) = ∫d⁴X (2π)^-2φ[X] e^+i(K·X) = ∫(cdt)(2π)^-1/2∫d³x (2π)^-3/2φ[ct,x] e^{+i(k·x - ωt)}
=============================

δ⁽⁴⁾[X - X'] = 1/(2π)⁴∫d⁴K e^{-i(K·(X-X'))} = δ[ct-ct']δ⁽³⁾[x - x'] = δ[ct-ct']δ[x-x']δ[y-y']δ[z-z']
δ⁽⁴⁾[X] = 1/(2π)⁴∫d⁴K e^-i(K·X) = δ[ct]δ⁽³⁾[x] = δ[ct]δ[x]δ[y]δ[z]
The Covariant 4D version of the Dirac Delta Function.
The 4D Delta function is defined as:
δ⁽⁴⁾[X - X'] = 1/(2π)⁴∫d⁴K e^{-i(K·(X-X'))} = δ[ct-ct']δ⁽³⁾[x - x'] = δ[ct-ct']δ[x-x']δ[y-y']δ[z-z'] {SI Units of [1/m⁴] for this case}

φ[X] = 1/(2π)⁴∫d⁴K φ̃[K] e^-i(K·X) = δ⁽⁴⁾[X] φ̃[K]

Some interesting mathematical results:
K·K = (k⁰,k)·(k⁰,k) = (k⁰k⁰-k·k) = (k⁰)²-|k|² = (k⁰+|k|)(k⁰-|k|)

δ[g[X]] = Σ_j(δ[X - X_j]/|g'[X_j]|) where all the roots of g[X] are assumed to be simple.

δ[(x²-α²)] = (2|α|)^-1( δ[x+a] + δ[x-a] )

δ[K·K] = δ[(k⁰)²-|k|²] = (2|k|)^-1( δ[(k⁰+|k|)] + δ[(k⁰-|k|)] )
=============================

(∂·∂)G[X - X'] = δ⁽⁴⁾[X-X']
δ⁽⁴⁾[X - X'] = 1/(2π)⁴∫d⁴Ke^{-i(K·(X-X'))} = δ[ct-ct']δ⁽³⁾[x - x'] = δ[ct-ct']δ[x-x']δ[y-y']δ[z-z']
∫_{[Some 4D Volume]}δ⁽⁴⁾[X - X']d⁴X = {1 if X'in the 4D Volume, 0 otherwise}
The Covariant 4D versions of the Green's Function and the Dirac Delta Function.
Given a linear ordinary differential equation (ODE), L(solution) = source, one can first solve

L (green) = δ s

, for each

s

,
and realizing that, since the source is a sum of delta functions, the solution is a sum of Green's functions as well, by linearity of

L

.
(∂·∂) has SI units of [1/m²]
G[X] has SI units of [1/m²]
G̃[K] has SI units of [m²]
δ⁽⁴⁾[X] has SI units of [1/m⁴], because we use (ct), not just (t)
d⁴X has SI units of [m⁴], because we use (ct), not just (t)

The Delta functions are defined as:
δ⁽¹⁾[x - x'] = 1/(2π) ∫dk e^-i(k(x-x'))
δ⁽³⁾[x - x'] = 1/(2π)³∫d³k e^{-i(k·(x-x'))}
δ⁽⁴⁾[X - X'] = 1/(2π)⁴∫d⁴K e^{-i(K·(X-X'))}

Temporarily, we will let (X' = 0) to simplify the math...

Green's function is defined as a point source for the 4D Laplacian, the D'alembertian.
(∂·∂)G[X] = δ⁽⁴⁾[X]

The 4D Delta function is defined as:
δ⁽⁴⁾[X] = 1/(2π)⁴∫d⁴K e^-i(K·X)

The 4D Fourier Transform of the Green's Function is defined as:
G[X] = 1/(2π)⁴∫d⁴K G̃[K] e^-i(K·X)

So:
G[X] = δ⁽⁴⁾[X] G̃[K]

(∂·∂)(1/(2π)⁴)∫d⁴K G̃[K] e^-i(K·X) = 1/(2π)⁴∫d⁴K e^-i(K·X)
(∂·∂)∫d⁴K G̃[K] e^-i(K·X) = ∫d⁴K e^-i(K·X)
∫d⁴K G̃[K](∂·∂) e^-i(K·X) = ∫d⁴K e^-i(K·X)
∫d⁴K G̃[K](-i)²(K·K) e^-i(K·X) = ∫d⁴K e^-i(K·X)
∫d⁴K G̃[K](-K·K) e^-i(K·X) = ∫d⁴K e^-i(K·X)

By taking the (∂·∂) inside the integral and equating factors:
G̃[K] = -1/(K·K)

Thus:
G[X] = -1/(2π)⁴∫d⁴K e^-i(K·X)/(K·K) = -δ⁽⁴⁾[X]/(K·K)

Alternately:
(∂·∂)G[X] = δ⁽⁴⁾[X] = 1/(2π)⁴∫d⁴K e^-i(K·X)
If we choose { ∂ = ±i K, the condition for 4D plane waves}
(±i K·±i K)G[X] = δ⁽⁴⁾[X] = 1/(2π)⁴∫d⁴K e^-i(K·X)
(±i)²(K·K)G[X] = δ⁽⁴⁾[X] = 1/(2π)⁴∫d⁴K e^-i(K·X)
(-1)(K·K)G[X] = δ⁽⁴⁾[X] = 1/(2π)⁴∫d⁴K e^-i(K·X)
So:
G[X] = -δ⁽⁴⁾[X]/(K·K) = -1/(2π)⁴∫d⁴K e^-i(K·X)/(K·K)

If the Differential Operator L = (∂·∂), the 4D Laplacian
Then Green's Function G = δ[t - r/c]/(4πr) = δ[t -|x - x'|/c]/(4πr)

If the Differental Operator L = ∇·∇, the 3D Laplacian
Then Green's Function G = -1/(4πr) = -1/(4π|x - x'|)

Eventually working into a Propagator Formalism:
G[X] = -1/(2π)⁴∫d⁴K e^-i(K·X)/(K·K) = - δ⁽⁴⁾[X]/(K·K)
G[X - X'] = -1/(2π)⁴∫d⁴K e^{-i(K·(X - X'))}/(K·K) = - δ⁽⁴⁾[X - X']/(K·K)

<< need to move this section >>
G[X - X'] = -(1/ћ²)/(2π)⁴∫d⁴P e^{-(i/ћ)(P·(X - X'))}/(P·P) = - (1/ћ)²δ⁽⁴⁾[X - X']/(P·P) = - (1/ћ)²δ⁽⁴⁾[X - X']/(E²/c² - p²)

G[X - X'] = (1/ћ²)/(2π)⁴∫d⁴P e^{-(i/ћ)(P·(X - X'))}(p² - E²/c²)

If Analytic Continuation is required, then
G[X - X'] = (1/ћ²)/(2π)⁴∫d⁴P e^{-(i/ћ)(P·(X - X'))}(p² - E²/c² ± iε)

see https://www.phy.duke.edu/~rgb/Class/Electrodynamics/Electrodynamics/node148.html
=============================

Sign[V] = TemporalDirection[V] = (V·T)/√[V·V] = v_o⁰/|v_o⁰| = { ( + 1) for future-pointing V, (-1) for past-pointing V}
The sign of the temporal component of a 4-Vector V is a Lorentz Scalar Invariant.
(V·T)/√[V·V] =
= (v⁰,v)·γ(1,β)/√[V·V]
= γ(v⁰ - v·β)/√[V·V]
= 1(v_o⁰ - v·0)/√[V_o·V_o]
= (v_o⁰)/√(v_o⁰)²
= (v_o⁰)/|(v_o⁰)|
=============================

SR Stress-Energy Tensor T_perfectfluid^μν = (ρ_eo + p_o)U^μU^ν/c² - p_oη^μν = (ρ_eo)V^μν - (p_o)H^μν
SpaceTime Projection Tensor (Minkowski Metric) η^μν = V^μν + H^μν
Temporal Projection Tensor V^μν = T^μ⊗T^ν = T^μT^ν = U^μU^ν/c²: Also known as the (V)ertical or tangential projection tensor
Spatial Projection Tensor H^μν = S^μ⊗S^ν = η^μν - V^μν = η^μν - T^μT^ν = η^μν - U^μU^ν/c²: Also known as the (H)orizontal or normal or orthogonal projection tensor
diagonal Projection Tensor D₁^μν = T^μ⊗S^ν = T^μS^ν: The 1st (D)iagnol projection tensor?
diagonal Projection Tensor D₂^μν = S^μ⊗T^ν = S^μT^ν: The 2nd (D)iagnol projection tensor?
Null (Unit) Projection Tensor N^μν = N^μ⊗N^ν = N^μN^ν = V^μν - (1/3)H^μν

Projection Tensor	Alt Name/Mnemonic	Definition / Representation	4-Divergence	Trace
SpaceTime η^μν	"(n)ow,here" Worldline Event	η^μν = ∂^μ[X^ν] = V^μν + H^μν → Diag[1,-1,-1,-1]	∂_μη^μν = 0^ν	Tr[η^μν] = 4
Temporal V^μν	"(V)ertical" Worldline Tangent	V^μν = T^μT^ν → Diag[1,0,0,0]	∂_νV^μν = = ∂_νT^μT^ν = T^ν∂_ν[T^μ] + T^μ∂_ν[T^ν] = (d/cdτ)[T^μ] + T^μ(∂·T) = A^μ/c² + T^μ(∂·T)	Tr[V^μν] = 1
Spatial H^μν	"(H)orizontal" Worldline Normal Hyperplanes orthogonal to Worldline	H^μν = η^μν - T^μT^ν → Diag[0,-1,-1,-1]	∂_μH^μν = -∂_μV^μν	Tr[H^μν] = 3
Null N^μν	"(N)ull" LightPath	N^μν = N^μN^ν = V^μν - (1/3)H^μν → Diag[1,1/3,1/3,1/3]	∂_μN^μν = = ∂_μ(V^μν - (1/3)H^μν) = ∂_μ(V^μν + (1/3)V^μν) = (4/3)∂_μV^μν	Tr[N^μν] = 0
Projection N̂^μν	(P)rojection to Hyperplanes orthogonal to N̂	N̂^μν = η^μν - N̂^μN̂^ν → ??

The SpaceTime Projection Tensor ( η^μν ) is the sum of the Temporal ( V^μν ) and Spatial ( H^μν ) Projection Tensors.
The Null Projection Tensor ( N^μν ) is a proportional sum which gives a trace of zero.
The Trace of each of these is a dimensional number.
see also: Newton-CartanTheory,

The 4-Divergence of the Temporal Projection Tensor gives:
∂_ν[V^μν] = T^ν∂_ν[T^μ] + T^μ∂_ν[T^ν] = (d/cdτ)[T^μ] + T^μ(∂·T) = (d/dτ)[U^μ]/c² + T^μ(∂·T) = A^μ/c² + T^μ(∂·T)

T_μ∂_ν[V^μν] = (∂·T) because T_μ(d/cdτ)[T^μ] = (1/2)(d/cdτ)[T_μT^μ] = (1/2)(d/cdτ)[1] = 0
This also means that T_μA^μ = (T·A) = 0, so basically T is temporal and A is spatial.

V^σ_μ∂_ν[V^μν] = V^σ_μ(A^μ/c² + T^μ(∂·T)) = (0^σ) + T_∥^σ(∂·T) = T_∥^σ(∂·T)
H^σ_μ∂_ν[V^μν] = H^σ_μ(A^μ/c² + T^μ(∂·T)) = A_⊥^σ/c² + (0^σ) = A_⊥^σ/c²
The Temporal and Spatial Projections of the 4-Divergence of the Temporal Projection Tensor.
We will use these to get Equations-of-Motion for the Stress-Energy Tensor.

The SpaceTime Projection Tensor ( η^μν ) is the sum of the Temporal ( V^μν ) and Spatial ( H^μν ) Projection Tensors.
The spatial projection tensor projects a 4-Vector onto the hyperplane orthogonal to the worldline.
Derivation:
Generic 4-Vector: V^μ
4-UnitTemporal: T = T^μ = γ(1,β)
Magnitude of V along T: V^μT_μ/(T^αT_α)
4-Vector Projection of V along T: V_∥^ν = (V^μT_μ)T^ν/(T^αT_α)
General Rule of Vectors: (V = V_∥ + V_⟂) or (V_⟂ = V - V_∥), Any vector is the sum of it's parallel and perpendicular parts.
4-Vector Projection of V orthogonal to T: V_⟂^ν = V^ν - V_∥^ν = V^ν - (V^μT_μ)T^ν/(T^αT_α)
V_⟂^ν = V^ν - (V^μT_μ)T^ν/(T^αT_α)
V_⟂^ν = V^μδ_μ^ν - (V^μT_μ)T^ν/(T^αT_α)
V_⟂^ν = V^μ(δ_μ^ν - T_μT^ν/(T^αT_α))
V_⟂^ν = V^μ(H_μ^ν) where H_μ^ν = (δ_μ^ν - T_μT^ν/(T^αT_α))
and finally, rasing the index...
H^μν = η^μβH_β^ν = η^μβ(δ_β^ν - T_βT^ν/(T^αT_α)) = (η^μβδ_β^ν - η^μβT_βT^ν/(T^αT_α)) = (η^μν - T^μT^ν/(T^αT_α))
H^μν = (η^μν - T^μT^ν/(T^αT_α)) is an orthogonal projection operator, which projects a given 4-Vector into the spatial hyper-plane orthogonal to the time direction.
Now, to simplify a bit...
(T^νT_ν) = 1 for the time-positive metric η^μν = ( + ,---), and (T^νT_ν) = -1 for the space-positive metric η^μν = (-, + + + )
H^μν = (η^μν - T^μT^ν) in the time-positive metric η^μν = ( + ,---) used throughout this article
H^μν = η^μν - V^μν = η^μν - T^μT^ν = η^μν - U^μU^ν/c²: Spatial (Horizontal) Projection
V^μν = T^μT^ν = U^μU^ν/c²: Temporal (Vertical) Projection
In a rest frame, H_(restframe)^μν = η^μν - T^μT^ν = η^μν - V_(restframe)^μν = Diag[1,-1,-1,-1] - Diag[1,0,0,0] = Diag[0,-1,-1,-1]
Thus,

Stress-Energy Tensor_{(perfect fluid)}T^μν = (ρ_eo + p_o)T^μT^ν - p_oη^μν
= ρ_eoT^μT^ν + p_oT^μT^ν - p_oη^μν
= ρ_eoT^μT^ν + p_o(T^μT^ν - η^μν)
= ρ_eoT^μT^ν - p_o(η^μν - T^μT^ν)
= (ρ_eo)V^μν + (-p_o)H^μν
= Stress-Energy Tensor_(dust) - p_oH^μν
Stress-Energy Tensor_{(perfect fluid_rest frame)} = ρ_eoDiag[1,0,0,0] - p_oDiag[0,-1,-1,-1] = Diag[ρ_eo,p_o,p_o,p_o]
So, if you take dust and add a projected spatial pressure onto it {negative due to (+,-,-,-) }, you get a perfect fluid.

Tr[η^μν] = η_μν[η^μν] = δ_ν^ν = 4
Tr[V^μν] = Tr[T^μT^ν] = η_μν[T^μT^ν] = [T^μη_μνT^ν] = [T_νT^ν] = 1
Tr[H^μν] = Tr[η^μν - T^μT^ν] = η_μν[η^μν - T^μT^ν] = η_μνη^μν -η_μνT^μT^ν = 4 - 1 = 3
Tr[N^μν] = Tr[V^μν - (1/3)H^μν] = η_μν[V^μν - (1/3)H^μν] = (1) - (1/3)(3) = 1 - 1 = 0

These Tensors can project a given 4-Vector onto the worldline ( V^μν ), or onto the 3D spatial hyperplane orthogonal to the worldline ( H^μν ).
This is known as (1 + 3) Splitting.
This is a coordinate-invariant way to separate Minkowski SpaceTime into (1) temporal component and (3) spatial components.
It is a tensorial way of separating a 4-Vector into components parallel and perpendicular to a specified direction.
*Note* One can use the Minkowski Diagram mnemonic that Time is in the "(V)ertical" direction, and Space is in the "(H)orizontal" directions,
used only as a SpaceTime Diagram analogy since we only have 3 pointing directions (and really only 2 on the 2D paper we draw on).
There is also a Null Projection Tensor for Photonic systems( N^μν ), and the fundamental SpaceTime Projection( η^μν ).

SR Light Cone

   | time-like interval(+)( V^μν )

   |    / light-like interval(0 = null)( N^μν )
worldline
.......|....... c       --- space-like interval(-)( H^μν )
\..future./
\....|..../
\..|../
\|/now,here( η^μν )
/|\
/..|..\    elsewhere
/....|....\
/...past...\
.......|...... -c

with:
( V^μν ) as the "Vertical" = Temporal Projection Tensor
( H^μν ) as the "Horizontal" = Spatial Projection Tensor
( N^μν ) as the "Null" = Lightlike Projection Tensor
( η^μν ) as the Minkowski Metric

One of the indices will be lowered in use as a projection operator.
Temporal case: T^μ = the 4-UnitTemporal
V^μσ = T^μT^σ
η_νσV^μσ = η_νσT^μT^σ
V^μ_ν = T^μT_ν

Spatial case: S'^μ = the 4-UnitSpatial {In the following we will take the 4-UnitSpatial S' to be "aligned" with the argument 4-Vector A}
H^μσ = η^μσ - T^μT^νσ
η_νσH^μσ = η_νση^μσ - η_νσT^μT^σ
H^μ_ν = η^μ_ν - T^μT_ν = η^μ_ν - V^μ_ν
H^μ_ν = δ^μ_ν - T^μT_ν = δ^μ_ν - V^μ_ν
H^μ_ν = S'^μS'ν

A^μ = A_parallel^μ + A_{perpendicular}^μ
A^μ = A_temporal^μ + A_spatial^μ
A^μ = A_∥^μ + A_⟂^μ

A_parallel^μ = A_temporal^μ = A_∥^μ = V^μ_νA^ν = T^μT_νA^ν = T^μ(T·A): Notice how this makes use of the Invariant Temporal Component Rule
A_{perpendicular}^μ = A_spatial^μ = A_⟂^μ = H^μ_νA^ν = (δ^μ_ν - V^μ_ν)A^ν = A^μ - A_∥^μ

Note, this is just basic Vector Addition and Vector Projection : A vector is the sum of its parallel and perpendicular components.
A = A_∥ + A_⟂
A^μ = A_∥^μ + A_⟂^μ
δ^μ_νA^ν = V^μ_νA^ν + H^μ_νA^ν
(δ^μ_ν = V^μ_ν + H^μ_ν)A^ν
δ^μ_ν = V^μ_ν + H^μ_ν
η^μ_ν = V^μ_ν + H^μ_ν
η^μν = V^μν + H^μν
So, our SpaceTime Minkowski Metric can be composed of the Temporal and Spatial Projection Operators.

V^μ_νA_∥^ν = T^μT_νA_∥^ν = T^μT_νT^ν(T·A) = T^μ(T_νT^ν) (T·A) = T^μ(1) (T·A) = T^μ(T·A) = A_∥^μ
The Temporal Projection Tensor acts like the Kronecker Delta Tensor on the Parallel Component 4-Vector.

H^μ_νA_⟂^ν = (δ^μ_ν - T^μT_ν)A_⟂^ν = (δ^μ_ν - T^μT_ν)(A^ν - A_∥^ν) = (δ^μ_νA^ν - δ^μ_νA_∥^ν - T^μT_νA^ν + T^μT_νA_∥^ν) = (A^μ - A_∥^μ - A_∥^μ + A_∥^μ) = (A^μ - A_∥^μ) = A_⟂^μ
The Spatial Projection Tensor acts like the Kronecker Delta Tensor on the Perpendicular Component 4-Vector.

V^μ_νA_⟂^ν = T^μT_νA_⟂^ν = T^μT_ν(A^ν - A_∥^ν) = T^μT_νA^ν - T^μT_νA_∥^ν = T^μT_νA_∥^ν - T^μT_νA_∥^ν = 0^μ
The Temporal Projection Tensor projects the Perpendicular Component 4-Vector into the 4-Zero.

H^μ_νA_∥^ν = (δ^μ_ν - T^μT_ν) A_∥^ν = (δ^μ_νA_∥^ν - T^μT_νA_∥^ν) = (A_∥^μ - A_∥^μ) = 0^μ
The Spatial Projection Tensor projects the Parallel Component 4-Vector into the 4-Zero.
η^μ_ν = V^μ_ν + H^μν
η^μ_νA^ν = V^μ_νA^ν + H^μ_νA^ν
η^μ_νA^ν = T^μT_νA^ν + S'^μS'_νA^ν
A^μ = T^μ(T·A) + S'^μ(S'·A)
A^μ = T^μ(a⁰) + S'^μ(|a_s|)
A = T(a⁰) + S'(|a_s|)

A·A =
= [T(a⁰) + S'(|a_s|)]·[T(a⁰) + S'(|a_s|)]
= [T(a⁰)·T(a⁰) + T(a⁰)·S'(|a_s|) + S'(|a_s|)·T(a⁰) + S'(|a_s|)·S'(|a_s|)]
= (a⁰)² T·T + 2(a⁰)(|a_s|)T·S' + (|a_s|)² S'·S'
= (a⁰)²(1) + 2(a⁰)(a)(0) + (|a_s|)²(-1)
= (a⁰)² - (|a_s|)²
The expected Lorentz Scalar

Continuing this same line of reasoning, and Rank-2 tensor can be separated into its component parts as well.
Let T^μν be a generic Rank-2 tensor.
Tensor T^μν

T⁰⁰	T⁰¹	T⁰²	T⁰³
T¹⁰	T¹¹	T¹²	T¹³
T²⁰	T²¹	T²²	T²³
T³⁰	T³¹	T³²	T³³

{The temporal region in blue, the spatial region in red, the mixed time-space regions in purple}
V_μνT^μν = (T_o)_μ(T_o)_νT^μν = (1,- 0)⊗(1,- 0)T^μν = T⁰⁰ = The Temporal Component
H_μνT^μν = (η_μν - V_μν)T^μν = (η_μνT^μν - V_μνT^μν) = Tr[T^μν] - T⁰⁰ = T¹¹ + T²² + T³³ = The Spatial Trace

J^ν = T_μT^μν = (T_o)_μT^μν = (1,- 0)T^μν = T^0ν = (T⁰⁰,T⁰¹,T⁰²,T⁰³) = The Temporal 4-Vector Part, which acts as a current
J^μ = T_νT^μν = (T_o)_νT^μν = (1,- 0)T^μν = T^μ0 = (T⁰⁰,T¹⁰,T²⁰,T³⁰) = The Temporal 4-Vector Part, which acts as a current

η_μνη^μν = Tr[η^μν] = 4
η_μνV^μν = Tr[V^μν] = 1
η_μνH^μν = Tr[H^μν] = 3

V_μνV^μν = T_μT_νT^μT^ν = (T_μT^μ)(T_νT^ν) = (1)(1) = 1
V_μνH^μν = V_μν(η^μν - V^μν) = Tr[V^μν] - V_μνV^μν = (1) - (1) = 0

H_μνV^μν = (η_μν - V_μν)V^μν = Tr[V^μν] - V_μνV^μν = (1) - (1) = 0
H_μνH^μν = (η_μν - V_μν)H^μν = Tr[H^μν] - V_μνH^μν = (3) - (0) = 3

A^μ = A_∥^μ + A_⟂^μ η^μ_ν = V^μ_ν + H^μ_ν η^μ_ν = T^μT_ν + S^μS_ν	SpaceTime 4-Vector A^μ	Temporal 4-Vector A_∥^μ	Spatial 4-Vector A_⟂^μ
SpaceTime Projection η^μ_ν	η^μ_νA^ν = A^μ	η^μ_νA_∥^ν = A_∥^μ	η^μ_νA_⟂^ν = A_⟂^μ
Temporal Projection V^μ_ν	V^μ_νA^ν = A_∥^μ = T^μ(T·A)	V^μ_νA_∥^ν = A_∥^μ	V^μ_νA_⟂^ν = 0^μ
Spatial Projection H^μ_ν	H^μ_νA^ν = A_⟂^μ = S^μ(S·A)	H^μ_νA_∥^ν = 0^μ	H^μ_νA_⟂^ν = A_⟂^μ
Null Projection N^μ_ν	N^μ_νA^ν = A_∠^μ = N^μ(N·A)

η^μν = V^μν + H^μν	SpaceTime Projection "(n)ow" η_μν	Temporal Projection "(V)ertical" V_μν	Spatial Projection "(H)orizontal" H_μν = η_μν - V_μν	Null Projection "(N)ull" N_μν = V_μν - (1/3)H_μν
SpaceTime Tensor η^μν	Tr[η^μν] = η_μνη^μν = 4	V_μνη^μν = 1	H_μνη^μν = 3	N_μνη^μν = 0
Temporal Tensor V^μν	Tr[V^μν] = η_μνV^μν = 1	V_μνV^μν = 1	H_μνV^μν = 0	N_μνV^μν = 1
Spatial Tensor H^μν	Tr[H^μν] = η_μνH^μν = 3	V_μνH^μν = 0	H_μνH^μν = 3	N_μνH^μν = -1
Null Tensor N^μν	Tr[N^μν] = η_μνN^μν = 0	V_μνN^μν = 1	H_μνN^μν = -1	N_μνN^μν = 4/3? Related I believe to the 4/3 problem of Electromagnetic Mass

Tensor Form	A^μη_μνB^ν	A^μV_μνB^ν	A^μH_μνB^ν
4-Vector Form	A·B	(A·B)_∥	(A·B)_⟂
Component Form	a⁰b⁰ - a·b	a⁰b⁰	-a·b

SpaceTime Projection	Tr[η^μ_αη^ν_β] = η^μ_αη_μνη^ν_β = η_αβ
Temporal Projection	Tr[V^μ_αV^ν_β] = V^μ_αη_μνV^ν_β = V_αβ
Spatial Projection	Tr[H^μ_αH^ν_β] = H^μ_αη_μνH^ν_β = H_αβ

Use of the Temporal and Spatial Projection Tensors becomes very apparent in the various forms of the Energy-Stress Tensor.
T_perfectfluid^μν = (ρ_eo)V^μν - (p_o)H^μν
V_μνT_perfectfluid^μν = V_μν[(ρ_eo)V^μν - (p_o)H^μν] = (ρ_eo)(1) - (p_o)(0) = ρ_eo
H_μνT_perfectfluid^μν = H_μν[(ρ_eo)V^μν - (p_o)H^μν] = (ρ_eo)(0) - (p_o)(3) = -3p_o
η_μνT_perfectfluid^μν = η_μν[(ρ_eo)V^μν - (p_o)H^μν] = (ρ_eo)(1) - (p_o)(3) = ρ_eo - 3p_o
ρ_eo = V_μνT_perfectfluid^μν
p_o = (-1/3)H_μνT_perfectfluid^μν
=============================

Stress-Energy Tensors T^μν: Symmetric
T_GRvacuum^μν = 0
T_{relativisticfluid}^μν = (ρ_eo)V^μν - (p_o)H^μν + (T^μQ^ν + Q^μT^ν) + Π^μν
T_perfectfluid^μν = (ρ_eo + p_o)U^μU^ν/c² - (p_o)η^μν = (ρ_eo + p_o)T^μT^ν - (p_o)η^μν = (ρ_eo)T^μT^ν - (p_o)H^μν = (ρ_eo)V^μν - (p_o)H^μν
   T_dust^μν = (ρ_eo)U^μU^ν/c² = (ρ_eo)T^μT^ν = (ρ_eo)V^μν
   T_vacuum^μν = -(p_o)η^μν = (ρ_eo)η^μν
   T_{radiation = nulldust}^μν = p_o(4U^μU^ν/c² - η^μν) = p_o(4T^μT^ν - η^μν) = p_o(4V^μν - η^μν) = (ρ_eo)[V^μν - (1/3)H^μν] = (ρ_eo)N^μν
T_{EM = photongas}^μν = (1/μ_o)(F^μαη_αβF^νβ - η^μνF_δγF^δγ/4) {aka. the Electrovacuum Solution}
Tr[T_perfectfluid^μν] = Tr[(ρ_eo + p_o)U^μU^ν/c² - p_oη^μν] = η_μν[(ρ_eo + p_o)U^μU^ν/c² - p_oη^μν] = [(ρ_eo + p_o)U^μη_μνU^ν/c² - p_oη_μνη^μν] = [(ρ_eo + p_o)c²/c² - p_o4] = [(ρ_eo + p_o) - 4p_o] = [ρ_eo - 3p_o]
Tr[T_dust^μν] = Tr[(ρ_eo)U^μU^ν/c²] = η_μν[(ρ_eo)U^μU^ν/c²] = [(ρ_eo)U^μη_μνU^ν/c²] = [(ρ_eo)c²/c²] = (ρ_eo)
Tr[T_vacuum^μν] = Tr[- p_oη^μν] = η_μν[- p_oη^μν] = [- p_oη_μνη^μν] = [- p_o4] = [- 4p_o] = (4ρ_eo)
Tr[T_radiation^μν] = Tr[p_o(4U^μU^ν/c² - η^μν)] = η_μν[p_o(4U^μU^ν/c² - η^μν)] = [p_o(4U^μη_μνU^ν/c² - η_μνη^μν)] = [p_o(4c²/c² - 4)] = [p_o(4 - 4)] = (0)
Tr[T_EM^μν] = Tr[(1/μ_o)(F^μαη_αβF^νβ - η^μνF_δγF^δγ/4)] = η_μν[(1/μ_o)(F^μαη_αβF^νβ - η^μνF_δγF^δγ/4)] = [(1/μ_o)( η_μνF^μαη_αβF^νβ - η_μνη^μνF_δγF^δγ/4)] = [(1/μ_o)(F_νβF^νβ - 4F_δγF^δγ/4)] = [(1/μ_o)(F_νβF^νβ - F_δγF^δγ)] = (0)
Tr[T_null-dust^μν] = η_μν kN^μN^ν = kN^μ η_μν N^ν = (0)
The energy-momentum of a single particle can be specified by a single 4-Vector.
However, the energy-momentum of a fluid requires a 2-index tensor, as neighbor interactions must be included.
In addition, one uses particle densities instead of discrete particles.
One can define a "Stress-Energy" Tensor T^μνas the flux of 4-Momentum P^μacross a surface of constant X^ν.
There are 4 main types:
T⁰⁰ is the flux of 4-Momentum P⁰ across a surface of constant X⁰, or flux of Energy across time, which is the energy density.
T⁰ⁱ is the flux of 4-Momentum P⁰ across a surface of constant Xⁱ, or flux of Energy across space, which is an energy flux (heat conduction).
Tⁱ⁰ is the flux of 4-Momentum Pⁱ across a surface of constant X⁰, or flux of i-Momentum across time, which is a momentum density (heat conduction).
T^ij is the flux of 4-Momentum Pⁱ across a surface of constant X^j, or flux of i-Momentum across space, which is a momentum flux (stress).
T^ij can be broken into 2 subtypes:
Tⁱⁱ is the flux of 4-Momentum Pⁱ across a surface of constant Xⁱ, or flux of i-Momentum across the {i = j}same direction in space, which is the isotropic pressure p = σⁱⁱ.
T^ij is the flux of 4-Momentum Pⁱ across a surface of constant X^j, or flux of i-Momentum across an {i ≠ j}orthogonal direction in space, which is a shear σ^ij.
T^μν is a symmetric tensor, so T⁰ⁱ = Tⁱ⁰{The energy flux = momentum density}, T^ij = T^ji, and the diagonal terms can be non-zero.
All cases below use : η^μν → Diag[+1,-1,-1,-1]

EnergyStressTensor T^μν Overall Units = [Energy Density]

Energy Density
ρ_mc² = ρ_e
time-time
T⁰⁰

T⁰⁰ρ_e = ρ_mc²

Energy Flux/c
s/c = cg
time-space
T^0j

T⁰¹cg^x

T⁰²cg^y

T⁰³cg^z

Momentum Density*c
cg = s/c
space-time
Tⁱ⁰

T¹⁰
cg^x

T²⁰
cg^y

T³⁰
cg^z

Momentum Flux = Spatial Stress
-σ^ij
space-space
T^ij

T¹¹ Pressure -σ^xx	T¹² Shear -σ^xy	T¹³ Shear -σ^xz
T²¹ Shear -σ^yx	T²² Pressure -σ^yy	T²³ Shear -σ^yz
T³¹ Shear -σ^zx	T³² Shear -σ^zy	T³³ Pressure -σ^zz

[The Stress-Energy Tensor - Generally {including shear stresses}] T^μν = (ρ_eo)V^μν + (-p_o)H^μν + (T^μQ^ν + Q^μT^ν) + Π^μν
T^μν =

ρ_eo	s_x/c	s_y/c	s_z/c
s_x/c	-σ_xx	-σ_xy	-σ_xz
s_y/c	-σ_yx	-σ_yy	-σ_yz
s_z/c	-σ_zx	-σ_zy	-σ_zz

where:
s = s_EM = s_e = (e x b)/μ_o = (e x h) is the Poynting vector.
σ_ij = ε_o[eⁱe^j + c²bⁱb^j - (1/2)δ^ij(e² + c²b²)] = ε_oeⁱe^j + (1/μ_o)bⁱb^j - (1/2)δ^ij(ε_oe² + (1/μ_o)b²)] is the Maxwell stress tensor.

================================================================
Tr[T_perfectfluid^μν] = Tr[(ρ_eo + p_o)U^μU^ν/c² - p_oη^μν] = η_μν[(ρ_eo + p_o)U^μU^ν/c² - p_oη^μν] = [(ρ_eo + p_o)U^μη_μνU^ν/c² - p_oη_μνη^μν] = [(ρ_eo + p_o)c²/c² - p_o4] = [(ρ_eo + p_o) - 4p_o] = [ρ_eo - 3p_o]

[For a Perfect Fluid {no spatial heat conduction, no viscosity}] where ρ_eo = rest energy density and p = p_o = rest pressure, (both of these are Lorentz Scalars)
T_perfectfluid^μν = (ρ_eo + p_o)U^μU^ν/c² - p_oη^μν = (ρ_eo + p_o)T^μT^ν - p_oη^μν = (ρ_eo)T^μT^ν - (p_o)H^μν = (ρ_eo)V^μν - (p_o)H^μν
T_perfectfluid^μν = (ρ_eo + p_o)U^μU^ν/c² - p_oη^μν = (h_o)U^μU^ν/c² - p_oη^μν : where Enthalpy Density (h_o) = (ρ_eo + p_o)
T_perfectfluid^μν = (ρ_mo + p_o/c²)U^μU^ν - p_oη^μν
T_perfectfluid^μν =

γ²(ρ_eo + p_o) - p_o	γ²(ρ_eo + p_o)u_x/c	γ²(ρ_eo + p_o)u_y/c	γ²(ρ_eo + p_o)u_z/c
γ²(ρ_eo + p_o)u_x/c	γ²(ρ_eo + p_o)u_xu_x/c² + p_o	γ²(ρ_eo + p_o)u_xu_y/c²	γ²(ρ_eo + p_o)u_xu_z/c²
γ²(ρ_eo + p_o)u_y/c	γ²(ρ_eo + p_o)u_xu_y/c²	γ²(ρ_eo + p_o)u_yu_y/c² + p_o	γ²(ρ_eo + p_o)u_yu_z/c²
γ²(ρ_eo + p_o)u_z/c	γ²(ρ_eo + p_o)u_xu_z/c²	γ²(ρ_eo + p_o)u_yu_z/c²	γ²(ρ_eo + p_o)u_zu_z/c² + p_o

T_o^μν{restframe} =

ρ_eo
	p_o
		p_o
			p_o

T_o^μν{restframe} =

T⁰⁰ = ρ_eo	T^0j = 0
Tⁱ⁰ = 0	T^ij = p_oδ^ij

T_o^μν{restframe} = Diag[ρ_eo,p_o,p_o,p_o] = Diag[u_eo,p_o,p_o,p_o]

The Lorentz Invariant Condition for a perfect fluid:
Tr[T_perfectfluid^μν] = T_ν^ν = η_μνT^μν = (T⁰⁰) - (T¹¹) - (T²²) - (T³³) = (ρ_eo) - (p_o) - (p_o) - (p_o) = ρ_eo - 3p_o
Tr[T_perfectfluid^μν] = Tr[(ρ_eo)V^μν - (p_o)H^μν] = [(ρ_eo)(1) - (p_o)(3)] = ρ_eo - 3po
This is essentially the scalar magnitude of the Tensor.
Notice the similarity with 4-Vectors:
Scalar Magnitude squared of Tensor T^μν: η_μνT^μν = T_ν^ν
Scalar Magnitude squared of 4-Vector A^μ: η_μνA^μA^ν = A_νA^ν
Generally for Perfect Fluid: T_perfectfluid^μν = (ρ_eo + p_o)U^μU^ν/c² - p_oη^μν = (ρ_eo + p_o)T^μT^ν - p_oη^μν = (ρ_eo)V^μν - (p_o)H^μν
Also: η_μνη^μν = η_ν^ν = δ_ν^ν = 4

There are several interesting Invariant scenarios ( Cosmological Equations of State ):
In increasing magnitudes of the Trace of the Energy-Stress Tensor, which I think is a more natural scale than how it is usually presented...
Tr[T^μν] = ρ_eo - 3p_o = 0 { p_o = ρ_eo/3, T^μν = (4ρ_eo/3)U^μU^ν/c² - (ρ_eo/3)η^μν = p(4U^μU^ν/c² - η^μν) = p(4U^μ/c² - ∂^μ)U^ν = (ρ_eo)N^μν }, represents light-like/null/photonic particles → Radiation Solution (also approx. Ultra-Relativistic Matter).
Tr[T^μν] = ρ_eo - 3p_o = ρ_eo - ε = ρ_eo - 3ρ_moRT = ρ_eo - 3ρ_moC² = ρ_moc² - 3ρ_moC² = { p_o = ρ_moRT = ρ_moC² = ρ_eo(C/c)², C<<c, C = √[RT] is characteristic thermal speed of molecules}, → Perfect Gas Solution.
Tr[T^μν] = ρ_eo - 3p_o = ρ_eo{ p_o = 0, T^μν = (ρ_eo)U^μU^ν/c² = (ρ_eo)V^μν}, then all magnitude comes from the energy/mass density of matter particles → Dust Solution.
Tr[T^μν] = ρ_eo - 3p_o = 2ρ_eo { p_o = -ρ_eo/3}, → Curvature Solution, which gives an Einstein Static Universe, but which we now know is not the case.
Tr[T^μν] = ρ_eo - 3p_o = 4ρ_eo{ p_o = -ρ_eo, T^μν = - pη^μν = + ρ_eoη^μν}, then all magnitude comes from the energy density*the Minkowski Metric → (Quantum) Vacuum /Dark Energy Solution.
see Stress-Energy Tensor,...
see Exact Solutions in GR, Fluid Solutions, Perfect Fluid, Dust Solution, Photon Gas (EM Radiation), Vacuum Solution, Electrovacuum Solution, ...
see Null Dust Solution, Scalar Field Solutions,...
see Friedmann–Lemaître–Robertson–Walker (FLRW) Metric

These are also often written in the Friedmann Equation form of {p_o = wρ_eo = wρ_moc²; n = 3(w + 1)}
where:
The line element is: ds² = g_μνdx^μdx^ν = (cdt)² - a²[t] dx²; a[t] is a "scale factor"
Hubble Parameter H = (ȧ/a)
ρ̇_m = -3(ȧ/a)(ρ_m + p/c²) = -3H(ρ_e + p/c²)
ä/a = -(4πG/3)(ρ_m + 3p/c²) + Λc²/3
Energy Density ρ_e ∝ a^{-3(w + 1)}
Volume V ∝ a³
For a spatially flat case (κ = 0): a[t] = a₀t^2/n
One can have a linear combination of terms: ρ_e ∝ Aa^-3 + Ba^-4 + Ca⁰
(c_s)² = (speed of sound)² = ∂p/∂ρ_m = w, for w = constant for a single form of perfect fluid
c_s = (speed of sound) = c * Sqrt[w]?

Perfect Fluid Stress-Energy Tensor T^μν = (ρ_eo)V^μν - (p_o)H^μν	Invariant Tr[T^μν] = (ρ_eo - 3p_o)	Pressure p_o = wρ_eo = wρ_moc²	Eqn. of State (EoS )Parm w = (p_o/ρ_eo) = (n/3)-1	n = 3(w + 1)	Energy Density ρ_eo falls off as a^-n = a^{-3(w + 1)}	a[t] = a₀t^2/n	Cosmological Solution eg. Matter Dominated, Radiation Dominated, etc.	Gravitational Pressure	Speed of Sound c_s = (speed of sound) = c * Sqrt[w]?	Dimensional Type
	< -2ρeo	> ρ_eo	>1	>6					Speed of Sound>Speed of Light = Unphysical
(ρ_eo)V^μν - (3ρ_eo/3)H^μν	-2ρ_eo	ρ_eo	1	6	ρ_eo ∝ a^-6		~Stiff Equation of State (Neutron Stars) ??
(ρ_eo)V^μν - (2ρ_eo/3)H^μν	-1ρ_eo	2ρ_eo/3	2/3	5	ρ_eo ∝ a^-5		???
	< 0ρeo	> ρ_eo/3	> 1/3	>4			"Ultralight", meaning ultra-photonic...			Unknown
(ρ_eo)V^μν - (1ρ_eo/3)H^μν = Null-Dust = (ρ_eo)N^μν = (p_o)(4V^μν - η^μν)	0ρ_eo	ρ_eo/3	1/3	4	ρ_R = ρ_eo ∝ a^-4	a[t] ∝ t^1/2	Radiation/~Ultra-Relativistic Matter/Soft Equation of State Null-Dust/Photon Gas/Hot Dust/Relativistic Neutrinos T^μν = (ρ_eo)N^μν			Relativistic Point
(ρ_eo)V^μν - ((v/c)²ρ_eo/3)H^μν	[1-(v/c)²]ρ_eo = (γ^-2)ρ_eo	(v/c)²ρ_eo/3 = v²ρ_mo/3 = ρ_moRT	{0..1/3}	{3..4}			Perfect Gas (\|v\|<<c) = Warm Dust v = v_th = √[3RT] = √[3K_BT/m] = {0..c} = characteristic rms 3D thermal speed of molecules essentially this smoothly varies from Matter-Dust (v~0) to Null-Dust (v~c)
(ρ_eo)V^μν - (0ρ_eo/3)H^μν = Matter-Dust = (ρ_eo)V^μν	1ρ_eo	0	0	3	ρ_M = ρ_eo ∝ a^-3	a[t] ∝ t^2/3	(Cold) Dust = (Incoherent) Matter/CDM/Baryons Normal Matter Einstein-de Sitter (EdS) solution T^μν = (ρ_eo)V^μν			Point
(ρ_eo)V^μν - (-1ρ_eo/3)H^μν	2ρ_eo	-ρ_eo/3	-1/3	2	ρ_eo ∝ a^-2	a[t] ∝ t	Curvature = Einstein Static Universe/?Cosmic Strings?	Replusive?	Imaginary, Instabilities	Line
	> 2ρ_eo	< -ρ_eo/3	< -1/3	< 2			Everything Below has Accelerating Expansion of Universe	Repulsive	Imaginary, Instabilities
(ρ_eo)V^μν - (-2ρ_eo/3)H^μν	3ρ_eo	-2ρ_eo/3	-2/3	1	ρ_eo ∝ a^-1	a[t] ∝ t²	??? ?Domain Walls?	Replusive	Imaginary, Instabilities	Sheet
(ρ_eo)V^μν - (-3ρ_eo/3)H^μν = Vacuum Energy = (ρ_eo)η^μν = -(p_o)η^μν	4ρ_eo	-ρ_eo	-1	0	ρ_Λ = ρ_eo ∝ a⁰ = constant	a[t] ∝ e^Ht _{with H = Hubble Const}	(Quantum) Vacuum Energy/Dark Energy /Cosmological Constant Λ/de Sitter/(Inflation~ -1) T^μν = (ρ_eo)η^μν	Replusive	Imaginary, Instabilities	Volume
	> 4ρ_eo	< -ρ_eo	< -1	< 0			Big Rip = Phantom Energy	Replusive	Imaginary, Instabilities Speed of Sound>Speed of Light = Unphysical	Unknown

A scalar field (φ) can be viewed as a sort of perfect fluid Equation-of-State (EoS) with w = [φ̇²/2 - V(φ)] / [φ̇²/2 + V(φ)] = {-1, ... , 1}
with ( φ̇ ) is the time derivative of (φ) and V(φ) is the potential energy.

A free scalar field (V=0) has w = 1,
and one with vanishing kinetic energy ( φ̇ →0) has w = -1, which is equivalent to a cosmological constant.
Any EoS in-between is achieveable, which makes scalar fields useful models of cosmological phenomena.

================================
[For Dust {no particle interaction}]
T_dust^μν = P^μN^ν = m_oU^μn_oU^ν = m_on_oU^μU^ν = ρ_moU^μU^ν = ρ_eoU^μU^ν/c² = ρ_eoT^μT^ν = (ρ_eo)V^μν
T_dust^μν = (ρ_eo)U^μU^ν/c² = (ρ_mo)U^μU^ν = n_om_oU^μU^ν = n_oU^μm_oU^ν = N^μP^ν
T_odust^μν{restframe} =

ρ_eo
	p = 0
		p = 0
			p = 0

{p = p_o = 0} for dust {matter particles do not interact, no pressure terms}
This is just a perfect fluid with the Lorentz Invariant Condition:
Tr[T^μν] = T_ν^ν = η_μνT^μν = ρ_eo = (T⁰⁰) - (T¹¹) - (T²²) - (T³³) = (ρ_eo) - (p) - (p) - (p) = ρ_eo - 3p = ρ_eo
Thus {p = 0}
*Note* We have simply gone from momentum of discrete particles P^ν = m_oU^ν to momentum density of a fluid T^μν = N^μ(m_oU^ν)
by using the 4-NumberDensity 4-Vector N^μ, where typically ∂_μN^μ = 0, The Particle # is conserved.

========================================
[For Vacuum {no particle interaction? = no (virtual?) particles?}]
T^μν = (ρ_eo)V^μν - (p_o = -ρ_eo)H^μν
T^μν = - p_oη^μν
T^μν = + ρ_eoη^μν = (ρ_eo)V^μν + (ρ_eo)H^μν
T_o^μν{restframe??} =

ρ_eo
	p = -ρ_eo
		p = -ρ_eo
			p = -ρ_eo

{p = -ρ_eo} for vacuum
This is just a perfect fluid with the Lorentz Invariant Condition:
Tr[T^μν] = T_ν^ν = η_μνT^μν = 4ρ_eo = (T⁰⁰) - (T¹¹) - (T²²) - (T³³) = (ρ_eo) - (p) - (p) - (p) = ρ_eo - 3p = 4ρ_eo
Thus {p = -ρ_eo}

===================================================================
[For Random Isotropic Radiation/Photons {no particle interaction??}]
T^μν = (ρ_eo)V^μν - (ρ_eo/3)H^μν = (ρ_eo)[V^μν - (1/3)H^μν] = (ρ_eo)[N^μν]
T^μν = (4ρ_eo/3)U^μU^ν/c² - (ρ_eo/3)η^μν
T^μν = p_o(4U^μU^ν/c² - η^μν)
T_o^μν{restframe??, where it is ?random?} =

ρ_eo
	p = ρ_eo/3
		p = ρ_eo/3
			p = ρ_eo/3

{p = (ρ_eo/3) = (ρ_moc²/3)} for isotropic radiation {particles do not interact} see Photon Gas
This is just a perfect fluid with the Lorentz Invariant Condition:
Tr[T^μν] = T_ν^ν = η_μνT^μν = 0 = (T⁰⁰) - (T¹¹) - (T²²) - (T³³) = (ρ_eo) - (p) - (p) - (p) = ρ_eo - 3p = 0
Thus {p = (ρ_eo/3) = (1/3) E_o/V_o = (1/3)n_oE_o}

===================================================================
[For ElectroMagnetic Field]

The Electromagnetic Stress-Energy Tensor
T^μν{no restframe /null} = (1/μ_o)[F^μαF^ν_α - (1/4)η^μνF_αβF^αβ] = (1/μ_o)[η_αβF^μαF^νβ - (1/4)η^μνF_αβF^αβ]

c²ρ_mo = ρ_eo = = (1/2)ε_o(e² + c²b²) = (1/2)(ε_oe² + b²/μ_o)	c g = s^j/c = cε_o(e x b) = (e x b)/(cμ_o)
c g = sⁱ/c = cε_o(e x b) = (e x b)/(cμ_o)	-σ^ij = -ε_o[eⁱe^j + c²bⁱb^j - (1/2)δ^ij(e² + c²b²)] = -[ε_oeⁱe^j + bⁱb^j/μ_o - (1/2)δ^ij(ε_oe² + c²b²/μ_o)] = The Maxwell Stress Tensor

This has the Lorentz Invariant Condition:
Tr[T^μν] = T_ν^ν = η_μνT^μν = + (T⁰⁰) - (T¹¹) - (T²²) - (T³³) = 0
= + ((1/2)ε_o(e² + c²b²)) - (-ε_o[e^xe^x + c²b^xb^x -(1/2)δ^xx(e² + c²b²)]) - (-ε_o[e^ye^y + c²b^yb^y -(1/2)δ^yy(e² + c²b²)]) - (-ε_o[e^ze^z + c²b^zb^z -(1/2)δ^zz(e² + c²b²)])
= (1/2)ε_o(e² + c²b²) + (ε_o[e^xe^x + c²b^xb^x + e^ye^y + c²b^yb^y + e^ze^z + c²b^zb^z]-3(1/2)ε_o(e² + c²b²)
= -(2/2)ε_o(e² + c²b²) + (ε_o[e^xe^x + e^ye^y + e^ze^z + c²b^xb^x + c²b^yb^y + c²b^zb^z]
= -ε_o(e² + c²b²) + ε_o(e² + c²b²)
= 0
Tr[T^μν] = 0, as expected for a null EM field
Alternately,
Tr[T^μν] = Tr[(1/μ_o)[F^μαF^ν_α - (1/4)η^μνF_αβF^αβ]]
= (1/μ_o)Tr[F^μαF^ν_α - (1/4)η^μνF_αβF^αβ]
= (1/μ_o)η_μν[F^μαF^ν_α - (1/4)η^μνF_αβF^αβ]
= (1/μ_o)[η_μνF^μαF^ν_α - (1/4)η_μνη^μνF_αβF^αβ]
= (1/μ_o)[F^μαη_μνF^ν_α - (1/4)(4)F_αβF^αβ]
= (1/μ_o)[F^μαF_μα - F_αβF^αβ]
= (1/μ_o)[F_μαF^μα - F_αβF^αβ]
= 0

F_den^μ = -∂_νT^μν = J_νF^μν
F_EMden = ( (j·e)/c, ρ(e) + (j⨯b) )
∂_ν = (∂_t/c,∇)

T^μν =

c²ρ_mo = ρ_eo	c g = s^j/c
c g = sⁱ/c	-σ^ij = -ε_o[eⁱe^j + c²bⁱb^j - (1/2)δ^ij(e² + c²b²)]

F_EMden⁰ = (j·e)/c = -∂_νT^0ν = -[(∂_t/c)(ρ_eo) + ∇·s/c]
(j·e) = -[(∂_t)(ρ_eo) + ∇·s]
∂_t[ρ_eo] + ∇·s + j·e = 0

F_EMdenⁱ = ρ(e) + (j⨯b) = -∂_νT^iν = -[(∂_t/c)(c g) - ∇·σ^ik]
ρ(e) + (j⨯b) = -[∂_t[g] - ∇·σ^ik]
∂_t[g] - ∇·σ^ik + ρ(e) + (j⨯b) = 0
∂_t[p_den] - ∇·σ^ik + ρ(e) + (j⨯b) = 0

Temporal Conservation Law:∂_t[ρ_eo] + ∇·s + j·e = 0
Spatial Conservation Law:∂_t[p_den] - ∇·σ^ik + ρ(e) + (j⨯b) = 0

==============================
For a fully-relativistic fluid
T_{relativisticfluid}^μν = (ρ_eo)V^μν - (p_o)H^μν + (T^μH^ν_σQ^σ + Q^σH^μ_σT^ν)/c + Π^μν
where:
(ρ_eo) = rest energy density (1 independent component)
(p_o) = (p) = invariant pressure (1 independent component)
T^μ = U^μ/c = UnitTemporal Worldline
V^μν = Temporal "(V)ertical" Projection Tensor
H^μν = Spatial "(H)orizontal" Projection Tensor
Q^μ = Heat Flux 4-Vector (with T_μQ^μ = 0, Heat Flux 4-Vector orthogonal to Worldline, 3 independent components)
Π^μν = Viscous Shear Tensor (Symmetric and Traceless, with T_μΠ^μν = 0, Viscous Shear Tensor orthogonal to Worldline, 5 independent components)

which gives a total of 10 independent components = max number of independent components of a rank 2 symmetric tensor like T_{relativisticfluid}^μν
see Fluid Solution,...

==========================
Perfect Fluid Stress-Energy Tensor
T^μν = (ρ_eo)V^μν - (p_o)H^μν
∂_νT^μν = ∂_ν[ρ_eo]V^μν + (ρ_eo)∂_ν[V^μν] - ∂_ν[p_o]H^μν - (p_o)∂_ν[H^μν]
∂_νT^μν = ∂_ν[ρ_eo]V^μν + (ρ_eo)∂_ν[V^μν] - ∂_ν[p_o]H^μν + (p_o)∂_ν[V^μν]
∂_νT^μν = ∂_ν[ρ_eo]V^μν + (ρ_eo + p_o)∂_ν[V^μν] - ∂_ν[p_o]H^μν

∂_ν[V^μν] = T^ν∂_ν[T^μ] + T^μ∂_ν[T^ν] = (d/cdτ)[T^μ] + T^μ(∂·T) = (d/dτ)[U^μ]/c² + T^μ(∂·T) = A^μ/c² + T^μ(∂·T)

T_μ∂_ν[V^μν] = (∂·T) because T_μ(d/cdτ)[T^μ] = (1/2)(d/cdτ)[T_μT^μ] = (1/2)(d/cdτ)[1] = 0
This also means that T_μA^μ = (T·A) = 0, so basically T is temporal and A is spatial.

V^σ_μ∂_ν[V^μν] = V^σ_μ(A^μ/c² + T^μ(∂·T)) = (0^σ) + T_∥^σ(∂·T) = T_∥^σ(∂·T)
H^σ_μ∂_ν[V^μν] = H^σ_μ(A^μ/c² + T^μ(∂·T)) = A_⊥^σ/c² + (0^σ) = A_⊥^σ/c²

Temporal Projection	Spatial Projection
V^σ_μ∂_νT^μν = V^σ_μ( ∂_ν[ρ_eo]V^μν + (ρ_eo + p_o)∂_ν[V^μν] - ∂_ν[p_o]H^μν ) ∂_ν[ρ_eo]V^σ_μV^μν + (ρ_eo + p_o)V^σ_μ∂_ν[V^μν] - ∂_ν[p_o]V^σ_μH^μν ∂_ν[ρ_eo]V^σ^ν + (ρ_eo + p_o)T_∥^σ(∂·T) - ∂_ν[p_o](0) T_∥^σT^ν∂_ν[ρ_eo] + (ρ_eo + p_o)T_∥^σ(∂·T) T_∥^σ[(d/cdτ)[ρ_eo] + (ρ_eo + p_o)(∂·T)] T_∥^σ[∂·[ρ_eoT] + (p_o)(∂·T)] T_∥^σ[∂·[ρ_eoU] + (p_o)(∂·U)]/c γ[∂_ν[ρ_eoU^ν] + (p_o)(∂_νU^ν)]/c	H^σ_μ∂_νT^μν = H^σ_μ( ∂_ν[ρ_eo]V^μν + (ρ_eo + p_o)∂_ν[V^μν] - ∂_ν[p_o]H^μν ) ∂_ν[ρ_eo]H^σ_μV^μν + (ρ_eo + p_o)H^σ_μ∂_ν[V^μν] - ∂_ν[p_o]H^σ_μH^μν ∂_ν[ρ_eo](0) + (ρ_eo + p_o)(A_⊥^σ/c²) - ∂_ν[p_o]H^σ^ν (ρ_eo + p_o)(A_⊥^σ/c²) - ∂_⊥^σ[p_o] ((ρ_eo + p_o)/c²)γ(cγ̇,γ̇u + γu̇)_⊥ - (∂_t/c, -∇)_⊥[p_o] ((ρ_eo + p_o)/c²)γ(γ̇u + γu̇) - (-∇)[p_o] γ((ρ_eo + p_o)/c²)(γ̇u + γu̇) + ∇[p_o]
Cool-Warm Dust Condition (p_o) << (ρ_eo) U_μ∂_νT^μν = Temporal Component ∂·(ρ_eoU) (∂_t[γρ_eo] + ∇·[γρ_eou]) (∂_t[ρ_e] + ∇·[ρ_eu]) = 0 if conserved	Cool-Warm Dust Condition (p_o) << (ρ_eo) H^σ_μ∂_νT^μν = Spatial Components γ((ρ_eo)/c²)(γ̇u + γu̇) + ∇[p_o] (ρ_m)(γ̇u + γu̇) + ∇[p_o] = 0 if conserved
Newtonian Limit: \|u\| << c (∂_t[ρ_e] - ∇·[ρ_eu]) Same as Warm Dust = 0 if conserved	Newtonian Limit: \|u\| << c, γ→1, γ̇→0 (ρ_m)(u̇) + ∇[p_o] (ρ_m)(a) + ∇[p_o] = = 0 if conserved

Euler Equations for Fluid Dynamics
Relativistic Euler equations
=============================

∂_νT^μν = Z^μ = Z = (0,0) = (0,0,0,0) {if conservative system}
∂_ν(X^αT^μν - X^μT^αν) = Z^αμ = [[0]]

∂_νT^μν = -F_den^μ = T^μν_,ν { = non-zero if non-conservative system, eg. it interacts with some other system; = 0 if conservative}
F_den^μ = -∂_νT^μν
∂_νT_EM^μν + F^μνJ_ν = 0 {The EM Stress-Energy Tensor relation with a 4-CurrentDensity}
In all cases above, if the Stress-Energy Tensor is conservative, we have the usual 4-Divergence[Stress-Energy Tensor] = 4-Zero.
This is actually 4 equations; Conservation of Energy + Conservation of Momentum for each spatial direction.
As in 3D, Force is the negative Gradient of a Potential
In addition, there is Conservation of Angular Momentum
=============================

Waves in SR - *Note* Modifications required for full GR
see Lanczos Tensor, The Physical Interpretation of the Lanczos Tensor, The Lanczos potential for the Weyl curvature tensor: existence, wave equation and algorithms,
see Gravitational Waves Demystified,

An interesting thing is that is takes 3 separate tensors to describe an SR wave.
Consider, a wave needs 4 parameters to be completely described.
The direction, frequency, amplitude and phase.
The direction and frequency are handled by the 4-WaveVector K = K^μ = (ω/c,k) = (ω/c,n̂ω/v_phase) = (ω/c,ωu/c²) = (ω/c)(1,β) = (1/cT,n̂/λ)
The phase is given by the interaction of the 4-WaveVector K with the 4-Position X = X^μ = (ct,x)
with the phase given by Φ = -(K·X)
However, the amplitude needs yet another tensor to describe it, and it can theoretically be any type of tensor: a scalar (C), a 4-Vector (C^μ), a (2,0)-Tensor (C^μν), etc.
ψ = (C)e^(iK·X) or (C^μ)e^(iK·X) or (C^μν)e^(iK·X)
The propagation is always handled by the e^(iK·X) = e^(-iΦ) term.

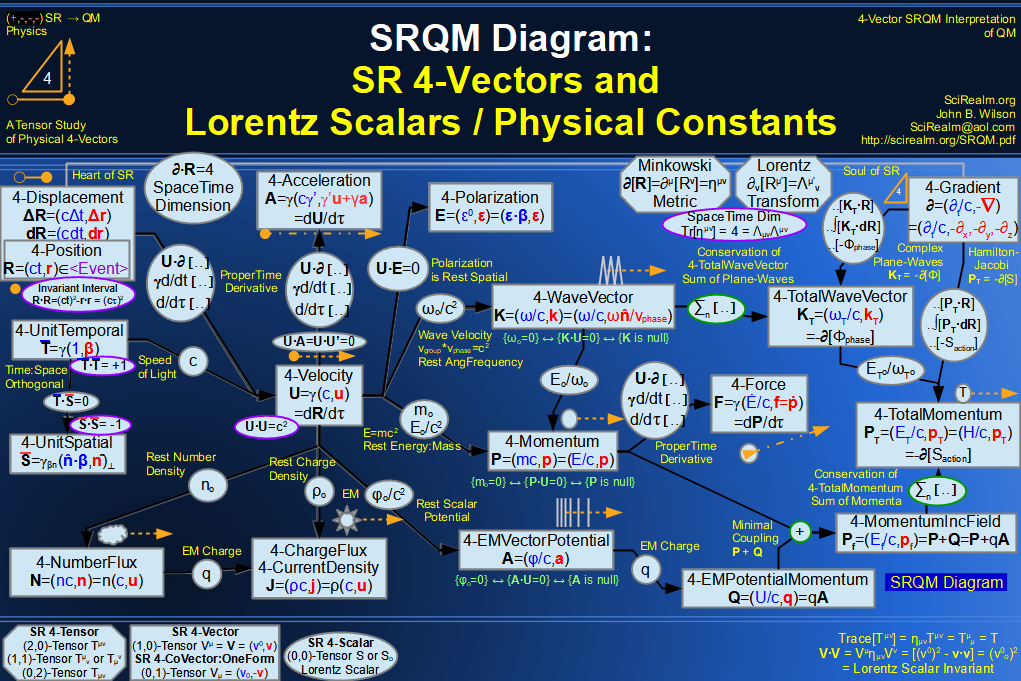
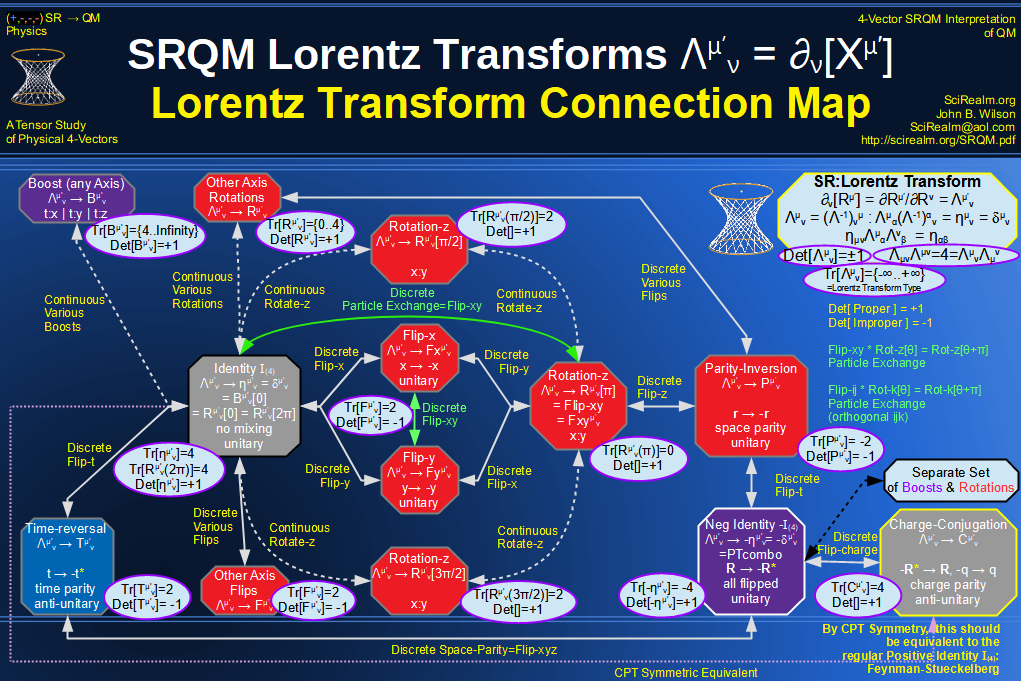
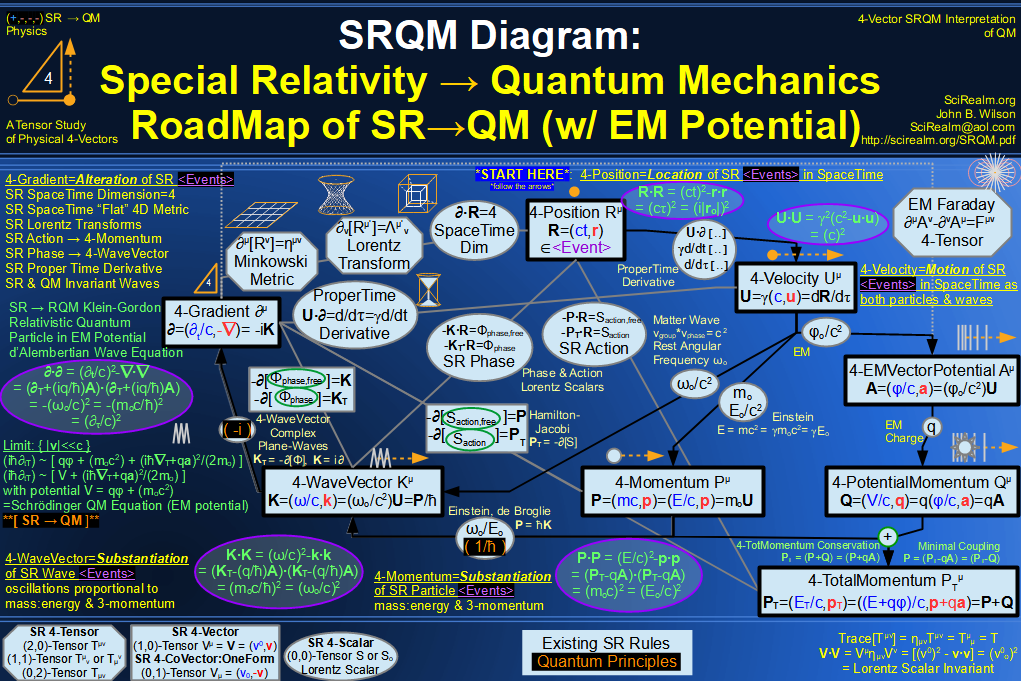
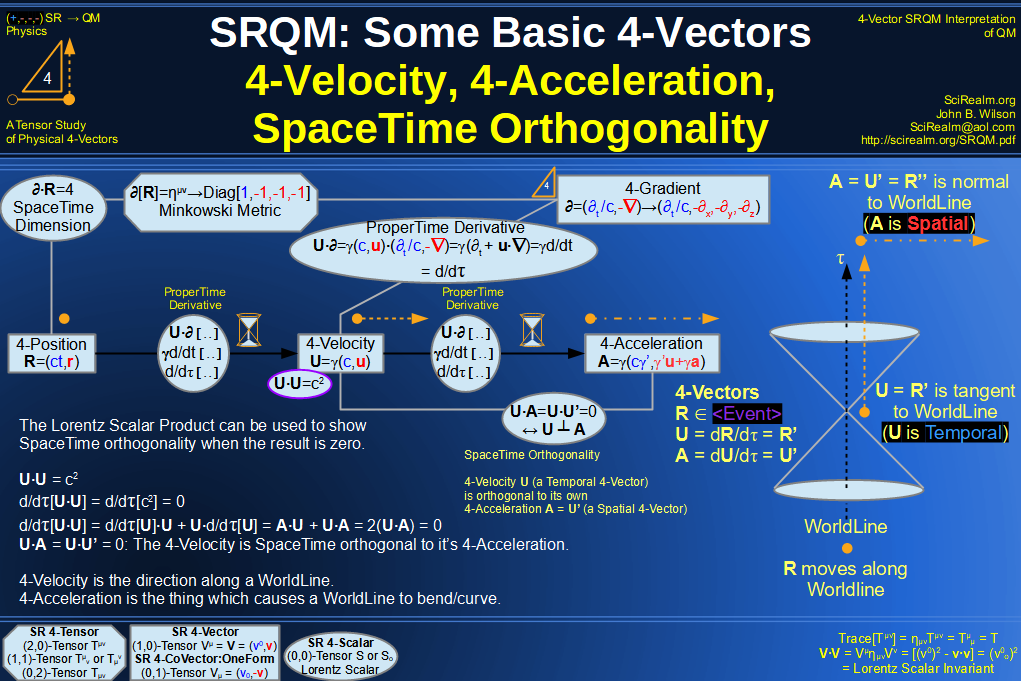
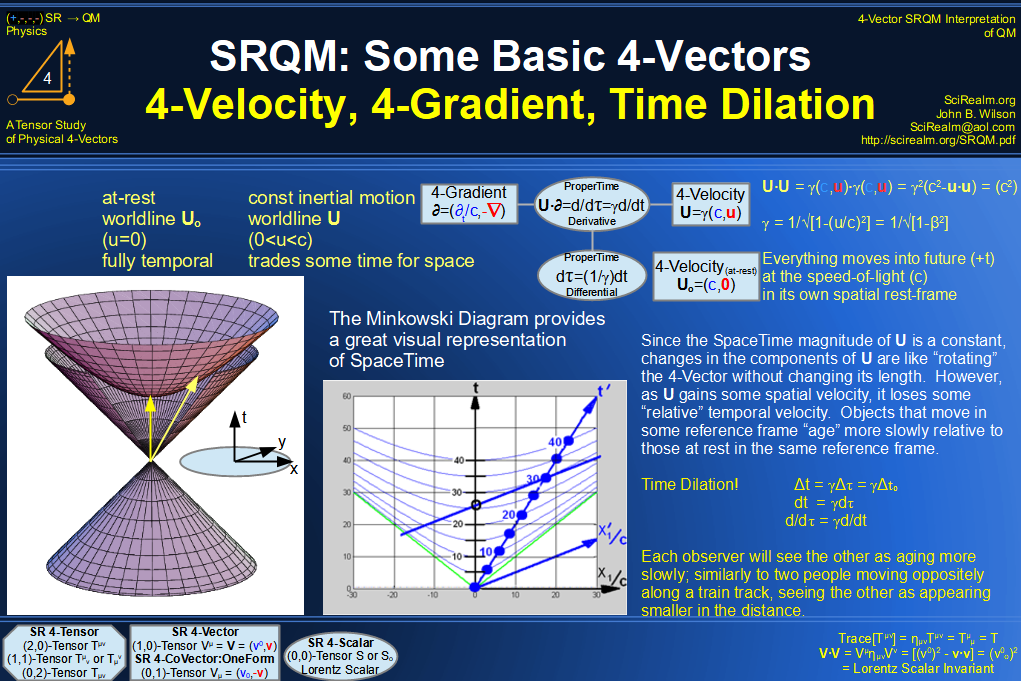
Wave Type:

Scalar Waves

Photonic/EM Waves (4-Vectors)

Gravitational Waves (2,0)-Tensors

Lanczos Potential Tensor
Gravitational Waves

Special Background Conditions:

None

Linearized Gravity = Weak Field limit
g^μν = η^μν + h^μν
where |h^μν| << 1
Minkowski SpaceTime limit
h^μν acts like Tensor Field propagating
in "flat" Minkowski SR

Field Type:

(0,0)-Tensor
= Scalar

(1,0)-Tensor
= 4-Vector

(2,0)-Tensor

(3,0)-Tensor

Field Identifier:

A = A^μ

h_TT^μν

H^μνρ or L^μνρ

Special Tensor Conditions:

None, 4 possible independent components.
Lorentz Invariant Conditions
will reduce # of independent component.

(h_TT^μν) = (h_TT^νμ)
h_TT^μν = h_TT^(μν)
Symmetric 2-Tensor
----
Reduces independent components
from 16 down to 10

Other Lorentz Invariant Conditions
will reduce it further

L^μνρ + L^νμρ = 0
L^μνρ = L^[μν]ρ
AntiSymmetric on first 2 indices

L^μνρ + L^ρμν + L^νρμ = 0
L^[μνρ] = 0
Jacobi/Bianchi Identity
----
Reduces independent components
from 64 down to 20

Other Lorentz Invariant Conditions
will reduce it further

Conservative Field Condition:
4-Divergence = 0
4-Divergenceless = Lorenz Gauge

Carroll also uses Lorenz Gauge for gravitational wave
in Intro to GR: SpaceTime and Geometry, pg. 301
Other names include:
Harmonic Gauge
Einstein Gauge
Hilbert Gauge
de Donder Gauge
Fock Gauge

N/A

(∂·A) = (∂_μA^μ) = 0

A is conserved

(∂·h_TT^μν)
= (∂_νh_TT^μν)
= (h_TT^μν_,ν)
= 0^μ

h_TT^μν is conserved

Lanczos differential gauge SR
(∂·L^μνρ)
= (∂_ρL^μνρ)
= L^μνρ_,ρ
= 0^μν

Purely Spatial Wave Condition:
Orthogonal to 4-Velocity U

(U·A) = (U_νA^ν) = 0 for a photonic wave

Generally
A_EM·U = (φ/c,a)·γ(c,u) = γ(φ - a·u) = φ_o
As we will see, this is a photonic wave and the
rest potential φ_o will be zero in the same way that
the rest mass m_o of a photon is zero
In other words:
There is no "at-rest" frame for light-like

(U·A) = 0 = γ(c,u)·(φ/c,a) = γ[φ - u·a] = 0
Therefore, φ = u·a
Therefore A = (u·a/c,a)
To an at-rest observer (u=0), A appears spatial A → (0,a)
To an â-null observer (u=câ), A appears null A → (|a|,a)
A 3rd situation is that u·a=0 via 3D orthogonality,
in which case A appears spatial A → (0,a)

(U·h_TT^μν) = (U_νh_TT^μν) = 0^μ

Traceless Condition:
Equivalent to Null = Photonic Condition:

Generally
A·A = (A^μη_μνA^ν) = (φ/c,a)·(φ/c,a) = (φ/c)² - a·a

From above, A = (u·a/c,a)
A·A = (u·a/c,a)·(u·a/c,a) = [(u·a/c)² - a·a)]
To an at-rest observer (u=0), A·A = (- a·a) appears spatial
To an â-null observer (u=câ), A·A = (0) appears null
A 3rd situation is that u·a=0 via 3D orthogonality,
in which case A appears spatial A → (0,a)
and A·A = (- a·a) appears spatial

Tr[ h_TT^μν ] = (η_μνh_TT^μν) = h_TTν^ν = 0

Lanczos algebraic gauge SR
Tr[ L_μν^ρ ]
= (η^ν_ρL_μν^ρ)
= ( L_μρ^ρ)
= 0_μ

Transverse Condition:
Occurs due to the combination of:
Solution is Free Plane Wave: gives K·K = 0, K is null
The Conservative Field Condition: gives K·C = 0
The Purely Spatial Condition: gives U_o·C = 0

The combination leads to the spatial k·c = 0
The wave is transverse

The Transverse-Traceless Gauge (TT)
aka. the Radiation Gauge

Wave Equation with Source:

(∂·∂)A^ν = μ_o J^ν

(∂·∂)h_TT^μν = -2 G^μν
(∂·∂)h_TT^μν = -16πG T^μν
I'm not sure about the signs
Also, this is linerized approx to GR

complicated

Wave Equation without Source:
ie. Freely-propagating

(∂·∂)Φ = 0

(∂·∂)A^ν = 0^ν

(∂·∂)h_TT^μν = 0^μν

(∂·∂)L^μνρ = 0^μνρ

Free Wave Solution:

Plane Wave with C or C^ν or C^μν or C^μνρ
as respective wave amplitudes

Φ = C e^(iK·X)

A^μ = C^μ e^(iK·X)

h_TT^μν = C^μν e^(iK·X)

L^μνρ = C^μνρ e^(iK·X)

Solution Check:
assumes that the wave amplitude C^... is a constant

(∂·∂)Φ
= η_ρσ ∂^ρ∂^σ C e^(iK·X)
= i η_ρσ ∂^ρK^σ C e^(iK·X)
= i² η_ρσ K^ρK^σ C e^(iK·X)
= - K_σK^σ Φ
= 0

(∂·∂)A^μ
= η_ρσ ∂^ρ∂^σ C^μ e^(iK·X)
= i η_ρσ ∂^ρK^σ C^μ e^(iK·X)
= i² η_ρσ K^ρK^σ C^μ e^(iK·X)
= - K_σK^σ A^μ
= 0^ν

(∂·∂)h_TT^μν
= η_ρσ ∂^ρ∂^σ C^μν e^(iK·X)
= i η_ρσ ∂^ρK^σ C^μν e^(iK·X)
= i² η_ρσ K^ρK^σ C^μν e^(iK·X)
= - K_σK^σ h_TT^μν
= 0^μν

(∂·∂)L^μνρ
= η_ρσ ∂^ρ∂^σ C^μνρ e^(iK·X)
= i η_ρσ ∂^ρK^σ C^μνρ e^(iK·X)
= i² η_ρσ K^ρK^σ C^μνρ e^(iK·X)
= - K_σK^σ L^μνρ
= 0^μνρ

Trivial Solution = No Wave = (Field = 0)

Φ = 0

A^μ = 0^μ

h_TT^μν = 0^μν

L^μνρ = 0^μνρ

Interesting Solution = Wave
4-WaveVector K is Null
Massless = LightLike = Photonic

K_σK^σ = 0

4-Divergenceless Check

4-WaveVector K orthogonal to 4-WaveAmplitude C^...
4-WaveVector K orthogonal to 4-Polarization E
4-WaveVector K orthogonal to Polarization Tensor

(∂·A) = (∂_μA^μ) = 0
∂_μC^μ e^(iK·X) = 0
iK_μC^μ e^(iK·X) = 0
K_μC^μ = 0

(∂·h_TT^μν) = (∂_νh_TT^μν) = 0^μ
∂_νC^μν e^(iK·X) = 0^μ
iK_νC^μν e^(iK·X) = 0^μ
K_νC^μν = 0^μ

(∂·L^μνρ) = (∂_ρL^μνρ) = 0^μν
∂_ρC^μνρ e^(iK·X) = 0^μν
iK_ρC^μνρ e^(iK·X) = 0^μν
K_ρC^μνρ = 0^μν

Examine Solutions:
general null K = (ω/c) (1,n̂)
assume null K = (ω/c,0,0,ω/c) in spatial z-direction

C = C^ν =
→ (0,c₁,c₂,0)

C^μν =
→

0	0	0	0
0	c₁₁	c₁₂	0
0	c₁₂	-c₁₁	0
0	0	0	0

0	0	0	0
0	h₊	h_x	0
0	h_x	-h₊	0
0	0	0	0

C^μνρ =
→...

Find Polarizations:

**Note**
The 4-Polarization E = C^ν
The Polarization Tensor C^μν
both can have complex components.

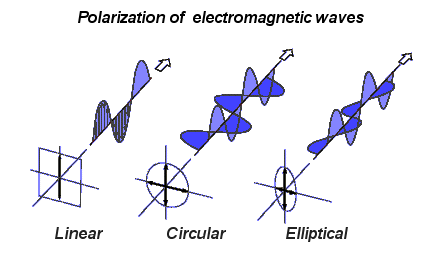
These give circular and elliptical polarizations
Circular/elliptical polarizations should also
carry angular momentum

Non-polarized

→ (0,c₁,c₂,0)
→ (0,c_x,c_y,0)
→ (0,1,0,0) = x-polarized
→ (0,0,1,0) = y-polarized (rotated 90°)

for photon travelling in z-direction
using the Jones Vector formalism n = z / |z|
and to the observer at rest
C = (0,1,0,0) : x-polarized linear
C = (0,0,1,0) : y-polarized linear
C = √[1/2] (0,1,1,0) : 45° from x-polarized linear
C = √[1/2] (0,1,i,0) : right-polarized circular
C = √[1/2] (0,1,-i,0) : left-polarized circular

General-polarized (elliptical) for z-photon
C = (0,Cos[θ]Exp[iα_x],Sin[θ]Exp[iα_y]),0)
C* = (0,Cos[θ]Exp[-iα_x],Sin[θ]Exp[-iα_y]),0)

h₊ = plus pattern
h_x = cross pattern (rotated 45°)
h_R = (1/√2)(h₊ + ih_x) = Right Circular
h_L = (1/√2)(h₊ - ih_x) = Left Circular

etc.
Presumably there could be
Elliptical polarizations for grav-waves
also

Test Particle Masses:
Plus (+) Polarization

Cross (x) Polarization

...

Based on this chart, we can create the freely-propagating Transverse-Traceless gravitational wave (far from source) a different way.
h_TT^μν = kA^μA^ν
In other words, in the same way that you can make a Null-Dust 2-Tensor, you can create a Gravitational Wave Potential from a tensor product of 2 photonic 4-VectorPotentials A^μ and A^ν.
Let the (k) factor in front be a dimensional Lorentz Scalar constant.
Then, all the extra Lorentz Invariant conditions that are chosen for the h_TT^μνtensor are the standard ones used for the 4-VectorPotential.
Just remember, this is only in the linearized gravity approximation, freely-propagating far from source.

A = A^μ	h_TT^μν = kA^μA^ν = kA^μ⊗A^ν
(∂·A) = (∂_μA^μ) = 0	(∂·h_TT^μν) = (∂_νh_TT^μν) = (∂_νkA^μA^ν) = k(∂_νA^ν)A^μ = k(0)A^μ = 0^μ
(U·A) = (U_νA^ν) = 0 for a photonic wave Generally A_EM·U = (φ/c,a)·γ(c,u) = γ(φ - a·u) = φ_o As we will see, this is a photonic wave and the rest potential φ_o will be zero in the same way that the rest mass m_o of a photon is zero In other words: There is no "at-rest" frame for light-like (U·A) = 0 = γ(c,u)·(φ/c,a) = γ[φ - u·a] = 0 Therefore, φ = u·a Therefore A = (u·a/c,a) To an at-rest observer (u=0), A appears spatial A → (0,a) To an â-null observer (u=câ), A appears null A → (\|a\|,a) A 3rd situation is that u·a=0 via 3D orthogonality, in which case A appears spatial A → (0,a)	(U·h_TT^μν) = (U_νh_TT^μν) = (U_νkA^μA^ν) = k(U_νA^ν)A^μ = k(0)A^μ = 0^μ
Generally A·A = (A^μη_μνA^ν) = (φ/c,a)·(φ/c,a) = (φ/c)² - a·a From above, A = (u·a/c,a) A·A = (u·a/c,a)·(u·a/c,a) = [(u·a/c)² - a·a] To an at-rest observer (u=0), A·A = (- a·a) appears spatial To an â-null observer (u=câ), A·A = (0) appears null A 3rd situation is that u·a=0 via 3D orthogonality, in which case A appears spatial A → (0,a) and A·A = (- a·a) appears spatial	Tr[ h_TT^μν ] = (η_μνh_TT^μν) = k(η_μνA^μA^ν) = k(A^μη_μνA^ν) = k[(u·a/c)² - a·a] If indeed (h_TT^μν = kA^μA^ν = kA^μ⊗A^ν) decomposes this way, we should get Tr[ h_TT^μν ] = 0^μ for the â-null observer Let me think on this a bit...

=============================

d/dτ[S] = (-A·S/c²)U
Fermi-Walker Transport and Thomas Precession of the 4-UnitSpatial.
The 4-UnitSpatial in its rest frame can be written as S_o = (0,s)
Let's look at the Lorentz transform for a boost in a general direction.
(a)' = (- γβa⁰ + (γ-1)(β·a)β/|β|² + a)
(a)' = (- γβa⁰ + (γ-1)(v·a)v/|v|² + a)
So, we can write for the 4-UnitSpatial
(s)' = (γ-1)(v·s)v/|v|² + s
Now, using { γ = 1/√[1 - (v/c)²] }
(γ-1)/|v|² = γ²/[c²(γ+1)]
So,
(s)' = (γ²/[c²(γ+1)])(v·s)v + s

Now, a mathematical trick:
Let's add a zero, but a special kind of zero, to the 4-Vector formula...
d/dτ[S] = (-A·S/c²)U + (U·S/c²)A
The (U·S) = 0 since the 4-Velocity is orthogonal to the 4-UnitSpatial
Why is this interesting?
Because...
d/dτ[s] = ω_T x s = k[ (a x u) x s ] = k[ (a·s)u - (u·s)a ] ;by the triple vector product rule
where k is a factor to be determined

(s)' = (γ²/[c²(γ+1)])(v·s)v + s
(s)'·u = (γ²/[c²(γ+1)])(u·s)u·u + s·u
(s)'·u = (1/[c²(γ+1)])(u·s)γ²u·u + s·u
(s)'·u = (1/[c²(γ+1)])(u·s)(γ²-1)c² + s·u
(s)'·u = (1/[c²(γ+1)])(u·s)(γ+1)(γ-1)c² + s·u
(s)'·u = (u·s)(γ-1) + s·u
(s)'·u = γ(u·s)
(s)' = γ(s)

d/dτ[s] ~ (a·s)u - (u·s)a = (a x u) x s
d/dτ[S] = (-A·S/c²)U + (U·S/c²)A
d/dτ[S] = (a_o·s/c²)U + (0)A
d/dτ[S] = (a_o·s/c²)U

Taking the spatial component:
d/dτ[s]? = (a_o·s/c²)γu

Ughhh - Thomas Precession is hard... I am all around it though
Need to get: ω_T = (γ²/[c²(γ+1)])(a x u)
Currently have: (s)' = (γ²/[c²(γ+1)])(u·s)u + s

=====================================================================
*********************************************************************
=====================================================================

Ok, now let's recap a bit...
We have looked at the SR formulas individually,
but let's examine them all together to notice similarities and differences.
Note also that all of these formula are Tensor equations, and therefore manifestly covariant,
meaning that they are all valid for all inertial observers, no matter what coordinates they may be using.

=====================================================================
*********************************************************************
=====================================================================

dR·dR = (cdτ)² or (0) or -(dr_o²), depending on the actual event interval
ΔR·ΔR = (cΔτ)² or (0) or -(Δr_o²), depending on the actual event interval
R·R = (cτ)² or (0) or -(r_o²), depending on the actual event interval
U·U = (c)²
A·A = -(a_o²)
P·P = (m_oc)² = (E_o/c)²
F·F = γ²[(Ė/c)² - f·f]
F_p·F_p = -(f_o²)
F_h·F_h = (γĖ_o/c)²
N·N = (n_oc)²
J·J = (ρ_oc)²
S·S = (s_oc)²
A·A = (φ_o/c)²
Q·Q = (U_o/c)²
P_T·P_T = (H_o/c)²
K·K = (ω_o/c)² = (1/cT_o)²
∂·∂ = (∂_τ/c)²

T·T = (1) Unit Temporal
T·S = (0) = N·N → They are orthogonal
S·S = (-1) Unit Spatial

Tr[η^μν] = 4
Tr[V^μν] = 1
Tr[H^μν] = 3
Tr[N^μν] = 0
Tr[T_perfectfluid^μν] = (ρ_eo - 3p_o)
Every Physical SR 4-Vector has Invariant Lorentz Scalar Products, typically giving an invariant "rest" value.
When the invariant "rest" value is 0, the 4-Vector is a Null Light-like Object.
Each 4-Vector Scalar Product with itself gives an Lorentz Invariant Magnitude squared.
The Trace Operator Tr[] gives the equivalent of the Lorentz Invariant Magnitude for a Rank-2 Tensor.
V·V = V^μ·V^ν = V^μ η_μν V^ν for 4-Vectors
Tr[T^μν] = η_μν T^μν for 4-Tensors
The Minkowski Metric η_μν is the defining operation in both cases.
=============================

η^μν = ∂^μ[X^ν] = Diag[[+1,-1,-1,-1]] {Cartesian form}
η_μν = Diag[[+1,-1,-1,-1]] {Cartesian form} = Scalar Product ( ^μ)·( ^ν) = Trace[^μν] = Tr[^μν]; [η^μν] = 1/[η_μν] for {μ = ν}; 0 for {μ ≠ ν}
The Minkowski metric is at the heart of SR, and essentially ties everything together.
It is how invariant scalar products are generated A·B = A^μη_μνB^ν
The Trace operator (η_μν) is the basically the scalar product rule for rank-2 tensors: Tr[C^μν] = η_μνC^μν = η_μνA^μB^ν = A^μη_μνB^ν = A·B = Lorentz Scalar
=============================

∂[X] = η^μν = ( )·( ) = The Scalar Product Dot and SpaceTime Projection Tensor
Tr[∂[X]] = Tr[η^μν] = η_μνη^μν = 4
∂·X = 4
∂·∂[X·X] = ∂·∂[(cτ)²] = 8
∂·∂[X] = ∂_μη^μν = 0^ν = (0,0) = Z
∂[X·X] = ∂[(cτ)²] = 2X
∂[∂[X]] = ∂[η^μν] = 0^ωμν
The 4-Gradient can be applied to the 4-Position in a number of different ways, eaching giving basic information about SR Minkowski SpaceTime.
=============================

P = (E/c)N = (|p|)N {massless = photonic case, |p| is a "momentum intensity", N is a "unit" 4-Null}
A = (φ/c)N = (|a|)N {massless = photonic case, |a| is a "vectorpotential intensity", N is a "unit" 4-Null}
K = (ω/c)N = (|k|)N {massless = photonic case, |k| is a "wavevector intensity", N is a "unit" 4-Null}
There are photonic (massless,null) versions of several of the 4-Vectors.
*Note*
P = m_oU = (mc)N = (γm_oc)N
m = (γm_o), where in the massless case {γ→∞ and m_o→0 in such a way that (m) is finite and non-zero}
Due to this, (|p|), (|a|), (|k|) are not Lorentz scalars, they are relativistic component quantities.
=============================

d/dτ[S] = (-A·S/c²)U
Fermi-Walker Transport and Thomas Precession of a 4-UnitSpatial (which could be a 4-Spin or 4-Polarization).
=============================

U·∂ = d/dτ = γ(d/dt)
---
U = dR/dτ = (U·∂)[R]
A = dU/dτ = (U·∂)[U]
U·dU/dτ = U·A = 0
F = dP/dτ = (U·∂)[P]
F_EMden^μ = dP_EMden^μ/dτ = J_νF^μν
G^μν = (X^μF^ν - X^νF^μ) = d/dτ[M^μν]
U·∂[Φ] = d/dτ[Φ] = -U·K = - ω_o : Phase rate of change is the negative angular frequency
U·∂[S] = d/dτ[S] = -U·P_T = - H_o : Action rate of change is the negative Hamiltonian { H = γH_o = γ(U·P_T) = -γd/dτ[S] }
One of the main Lorentz Scalar Invariants (U·∂) =(d/dτ) = the derivative wrt. Proper Time
It is used to generate 4-Vectors from 4-Vectors and Lorentz Scalars from Lorentz Scalars
P_T = (H/c,p_T) = - ∂[S] = (-∂_t[S]/c,∇[S])
=============================

Σ*[P_(n)] = 0, {where the Σ* counts pre-collision terms positively and post-collision terms negatively}
P_T_particle = P + qA, {the sum of inherent particle momentum and charged interaction potential momentum}
P_T_sys = Σ_n[P_Tparticle(n)], {the sum of all particle momenta in the system}
M_Tsys^μν = Σ_n[M_particle(n)^μν], {meaning the Total AngularMomentum is the sum of all individual AngularMomenta in the system}
P₁ + P₂ = P₁' + P₂' : Conservation of 4-Momentum
P₁·P₂ = P₁'·P₂' : The Elastic Collision Lemma
Conservation of 4-TotalMomentum and 4-TotalAngularMomentum plays a key role in all of physics.
=============================

U_μη^μν = U^ν
U_μV^μν = U^ν
U_μH^μν = 0^νU_μN^μν = U^ν
U·U = (c)²
U·∂ = d/dτ = γ(d/dt)
U·ΔX = c²Δτ
U·dU/dτ = U·A = 0
U·F = γ_fĖ_o = γ_fṁ_oc²
U·F_EM = 0 {because F_EM is a pure (space-like) force}
U·P = E_o
U·P_T = H_o
U·A_EM = φ_o
U·J = ρ_oc²
U·K = ω_o
U·Ε = 0 {photon polarization, the polarization is orthogonal to direction of motion}
U·h_TT^μν = 0 {gravitational wave polarization, the polarization is orthogonal to direction of motion}
U·T_EM^μν = c²G
U·F^μν = F_EM/q
U·F^μν = H_ν^μJ^ν/σ
Many of the relations are just the "Invariant Rest Value of the Temporal Component Rule", where you take a scalar product with a 4-Velocity U.
Similarly, a contraction of the 4-Velocity with a (2,0)-Tensor, gives a 4-Vector, which is itself a (1,0)-Tensor.
Anytime the result is zero, then the two 4-Vectors are orthogonal. The other 4-Vector is thus space-like.
=============================

U = dR/dτ = (U·∂)[R]
---
A = dU/dτ = (U·∂)[U]
P = m_oU = (E_o/c²)U Einstein's famous (E = mc²)
N = n_oU
J = ρ_oU = qn_oU = qN
K = (ω_o/c²)U
A_EM = (φ_o/c²)U
A_EM = (q/4πε_oc[R·U]_ret)U {for a point charge}
Many of the relations are just a Lorentz Scalar (1 independent component) times the 4-Velocity U (3 independent components),
giving a resultant 4-Vector which has (4 independent components).
=============================

J = (ρ_o/n_o)N = (q)N
J = (ρ_o/m_o)P or P = (m_o/ρ_o)J
K = (ω_o/E_o)P or P = (E_o/ω_o)K or hint hint...
Since many of the 4-Vectors are Lorentz Scalar proportional to 4-Velocity U, they will be proportional to one another via Lorentz Scalars.
=============================

<chargedensity>U = <charge>n_oU = <charge>N = <Charge>Flux = <Current>Density
G = μ_moU = m_on_oU = m_oN = Mass Flux = MomentumDensity
S = s_oU = S_entn_oU = S_entN = Entropy Flux
J = ρ_oU = qn_oU = qN = Charge Flux = CurrentDensity
Likewise, several 4-Vectors are *charge* proportional to the 4-NumberFlux N, and *charge_density* proportional to the 4-Velocity U.
=============================

∂·X = 4
∂_μη^μν = 0^ν
∂_μV^μν =A^μ/c² + T^μ(∂·T)
∂_μH^μν = -∂_μV^μν
∂_μN^μν = (4/3)∂_μV^μν ∂·K = 0 {if conservative}
∂·J = (∂_t/c,-∇)·(ρc,j) = (∂_tρ + ∇·j) = ? = 0 {if conservative}
∂·U = (∂_t/c,-∇)·γ(c,u) = ( ∂_tγ + ∇·[γu] ) = ( ∂_tγ + γ(∇·u) + (u·∇[γ] ) ) = ? = 0 {if conservative}
∂·A_EM = (∂_t/c,-∇)·(φ/c,a) = (∂_tφ/c² + ∇·a) = 0 {In the Lorenz Gauge, which is the case for an EM potential}
∂_νh_TT^μν = 0^μ {if conservative} (Lorenz Gauge for a free Gravitational Wave)
∂·J_EM = 0 {if conservative, which is the case for an standard EM current}
∂·N = 0 {if conservative, which is the case for the particle count of a Perfect Fluid}
∂·S = 0 {if conservative, which is the case for the entropy of a Perfect Fluid}
∂·F^αν = μ_oJ
∂_αF^αν = μ_oJ^νand ∂^αF^μν + ∂^νF^αμ + ∂^μF^να = 0
∂_νT^μν = 0^μ = Z = (0,0) {if conservative} (Conservation of Energy and Linear Momentum in the Stress-Energy Tensor)
∂_νT^μν = -F_den^μ = T^μν_,ν { = non-zero if non-conservative system, eg. it interacts with some other system}
∂_ν(X^αT^μν - X^μT^αν) = Z^αμ = [[0]], {if conservative} (Conservation of Angular Momentum in the Stress-Energy Tensor)
∂_νM^μν = 0^ν = Z = (0,0) {if conservative} (Conservation of Centroid and Angular Momentum)
The 4-Divergence ∂ is used quite often, and anytime the result is zero indicates a conservative system (no sinks or sources).
=============================

	Lorentz Scalar <Potential>	4-Vector = -Gradient[<Potential>]	Rest value Temporal Component
SR Phase (Φ)	Φ = -(K·R)	4-WaveVector K = -∂[Φ]	U·K = -U·∂[Φ] = -d/dτ[Φ] = ω_o
SR TotalPhase (Φ_T)	Φ_T = -(K_T·R)	4-TotalWaveVector K_T = -∂[Φ_T]	U·K_T = -U·∂[Φ_T] = -d/dτ[Φ_T] = ω_To
SR Action (S_act)	S_act = -(P_T·R)	4-TotalMomentum P_T = -∂[S_act]	U·P_T = -U·∂[S_act] = -d/dτ[S_act] = H_o
			U·P_Tden = -L_deno = n_o(P_T·U) = H_deno
SR Stress-Energy (T^μν)	eg. T_perfectfluid^μν = (ρ_eo)V^μν - (p_o)H^μν	4-ForceDensity F_den^μ = -∂_ν[T^μν]	U_μF_den^μ = -U_μ∂_ν[T^μν] = γ_fĖ_o = γ_fṁ_oc²
The magic behind the EM curtain...		∂^ν[P_T^μ] = q∂^μ[A_EM^ν]

Some very important and analytical 4-Vector relations can be defined via 4-Gradient function.
=============================

S_act = -(P_T·R) or S = -(P_T·X) and ∂[S] = -P_T.
S_act = -∫(P_T·dR) = -∫(P_T·dR/dτ)dτ = -∫(P_T·U)dτ = -∫(P_T·U/γ) dt = ∫L dt
( γ - 1/γ ) = (γβ²) : Relativistic Identity
γ(P_T·U) + -(P_T·U)/γ = (γβ²)(P_T·U)
H + L = p_T·u
H = γ(P_T·U)
L = -(P_T·U)/γ
H/γ = γ(P_T·U)/γ = (P_T·U) = H_o :The Rest Hamiltonian
γL = -γ(P_T·U)/γ = -(P_T·U) = L_o :The Rest Lagrangian
H_o + L_o = 0
L_deno = -n_o(P_T·U) = (n_o)(-P_T·U) = (n/γ)(γL) = nL = n_oL_o
Advanced Mechanics Concepts (Action S, Lagrangian L, Hamiltonian H) can be put into Lorentz Invariant form (S, γL = L_o, H/γ = H_o).
(H + L = p_T·u), so (H_o + L_o = 0)
=============================

Ε*·Ε = -1
Ε·K = 0
alternately Ε·U = 0
Polarization States (unit spatial vectors orthogonal to direction of motion) can be understood as simple Lorentz Invariant conditions,
upon which all observers must agree. The 4-Polarization must be a spatial 4-Vector.
M^μνP_ν = 0 {Fokker-Synge Equation}
alternately M^μνU_ν = 0
The same thing applies for internal Ang.Momentum (2,0)-Tensor M^μν.
Essentially, in both the 4-Vector and (2,0)-Tensor case, we want a space-like geometric object which remains orthogonal to the time-like U or P or K for all observers.
=============================

∂·A = (∂_t/c,-∇)·(φ/c,a) = (∂_tφ/c² + ∇·a) = 0 : The Lorenz Gauge for Classical EM - Yes, Lorenz, not Lorentz.
X·A = (ct,x)·(φ/c,a) = (tφ - x·a) = 0 : The Fock-Schwinger Gauge (Relativistic Poincaré Gauge).
A·A = (φ/c,a)·(φ/c,a) = (φ/c)² - a·a = (φ_o/c)² = constant : The Dirac Gauge
gives the analogous Potential-Vector Potential equation.
There exist Lorentz Invariant/Covariant Gauge Conditions.
*Note* There also exist non-covariant/incomplete gauges
(φ) = 0 : The Weyl Gauge (Hamiltonian Gauge/Temporal Gauge)
(∇·a) = 0 : The Coulomb Gauge (Transverse Gauge)
These are just the temporal and spatial components of the Lorenz Gauge set to zero individually.
(r·a) = 0 : The Multipolar Gauge (Line Gauge/Point Gauge/Poincaré Gauge)
see Gauge Fixing,
=============================

Symmetric SR (2,0)-Tensors:
Minkowski Metric Tensor η^μν = ∂^μ[X^ν] = Diag[[+1,-1,-1,-1]]; η_μν = Diag[[+1,-1,-1,-1]] = Scalar Product ( )·( ) = Trace[] = Tr[]; [η^μν] = 1/[η_μν] for {μ = ν}; 0 for {μ ≠ ν}
Temporal Projection Tensor = V^μν = T^μT^ν = U^μU^ν/c²
Spatial Projection Tensor H^μν = η^μν - V^μν = η^μν - T^μT^ν = η^μν - U^μU^ν/c²
SpaceTime Projection Tensor η^μν = V^μν + H^μν
Null Projection Tensor N^μν = V^μν - (1/3)H^μνStress-Energy Tensor_{(perfect fluid)}T_perfectfluid^μν = (ρ_eo + p_o)U^μU^ν/c² - p_oη^μν = (ρ_eo + p_o)T^μT^ν - p_oη^μν = (ρ_eo)T^μT^ν - (p_o)H^μν = (ρ_eo)V^μν - (p_o)H^μν
Stress-Energy Tensor_(dust)T_dust^μν = ρ_eoU^μU^ν/c² = ρ_eoT^μT^ν = (ρ_eo)V^μν
Stress-Energy Tensor_(vacuum)T_vacuum^μν = - p_oη^μν = + (ρ_eo)η^μν
Stress-Energy Tensor_{(radiation = null dust)}T_radiation^μν = p_o(4U^μU^ν/c² - η^μν) = p_o(4T^μT^ν - η^μν) = p_o(4V^μν - η^μν) = (ρ_eo)N^μν = (ρ_eo)[V^μν - (1/3)H^μν]
Stress-Energy Tensor_{(EM = photon gas)}T_EM^μν = (1/μ_o)(F^μαη_αβF^νβ - η^μνF_δγF^δγ/4)
The Kronecker Delta 4-Tensor = δ^μ_ν = η^μ_ν = η^μαη_αν : (1 if μ = ν; 0 if μ ≠ ν; μ,ν = [0..3]) {also the LorentzTransform*InverseLorentzTransform (Λ^ρ_ν'Λ^ν'_β) = δ^ρ_β }
The Kronecker Delta 3-tensor = δ^j_k : (1 if j = k; 0 if j ≠ k; i,j = [1..3])
Gravitational Wave Tensor h^μν
Technically this is a "perturbation" on the Minkowski Metric, where the "flat SpaceTime limiting case" of gravitational waves act like plane waves in the SpaceTime manifold.
g^μν = η^μν + h^μν where |h^μν| << 1

Anti-Symmetric SR (2,0)-Tensors:
Faraday EM Tensor F^μν = (∂^μA_EM^ν - ∂^νA_EM^μ)
Relativistic Angular Momentum Tensor M^μν = (X^μP^ν - X^νP^μ)
Relativistic Torque (4-Couple) Tensor G^μν = (X^μF^ν - X^νF^μ) = d/dτ[M^μν]
The Levi-Civita (Cyclic Permutation) 4-Tensor = ε_μνρσ, (1 if even permutation; -1 if odd permutation; 0 if no permutation; totally anti-symmetric; [0..3])
The Levi-Civita (Cyclic Permutation) 3-tensor = ε_jkl, (1 if even permutation, -1 if odd permutation, 0 if no permutation; totally anti-symmetric; [1..3])
Important SR (2,0)-Tensors can be constructed from the SR 4-Vectors, which are themselves (1,0)-Tensors.
Interestingly, they appear to be grouped into Symmetric and Anti-Symmetric Types.

We can always break a rank-2 tensor into a sum of a symmetric and anti-symmetric tensor.
T^μν = (T^μν + T^νμ)/2 {symmetric} + (T^μν -T^νμ)/2 {anti-symmetric}
For the 4x4 = 16 case, this breaks down into symmetric (at most 10 independent components) + anti-symmetric (at most 6 independent components).
Importantly, A symmetric tensor contracted with an anti-symmetric one gives zero.
=============================

Stress-Energy Tensor_(dust) T_dust^μν = (ρ_eo)V^μν
Stress-Energy Tensor_(vacuum) T_vacuum^μν = (ρ_eo)η^μν
Stress-Energy Tensor_{(radiation = null dust)} T_radiation^μν = (ρ_eo)N^μν
Three special cases of the Perfect Fluid Stress-Energy Tensor can be simplified greatly using Projection Tensors
Stress-Energy Tensor_{(AllPressure)} T_AllPress^μν = (-p_o)H^μν
An interesting case with zero energy density = All pressure *Maybe a Dark Energy thing???*
=============================

F_EM^μ = dP^μ/dτ = qU_ν(∂^μA_EM^ν - ∂^νA_EM^μ) = qU_νF^μν
H_ν^μJ^ν = σU_νF^μν
P_den^μ = G ^μ = n_oP ^μ = n_om_oU ^μ = (n_oE_o/c²)U ^μ = ρ_moU ^μ = U_νT^μν/c²
D^αβ = (1/μ_o)F^αβ - M^αβ
Some 4-Vectors are made via more complicated expressions involving (2,0)-Tensors, which are themselves constructed from (1,0)-Tensors
=============================

T_perfectfluid^μν = (ρ_eo + p_o)U^μU^ν/c² - p_oη^μν = (ρ_eo + p_o)T^μT^ν - p_oη^μν = (ρ_eo)T^μT^ν - (p_o)H^μν = (ρ_eo)V^μν - (p_o)H^μν
T_dust^μν = ρ_eoU^μU^ν/c² = ρ_eoT^μT^ν = (ρ_eo)V^μν, because Tr[T_dust^μν] = (ρ_eo), which gives {p_o = 0}
T_vacuum^μν = - p_oη^μν, because Tr[T_vacuum^μν] = (4ρ_eo), which gives {p_o = -ρ_eo}
T_radiation^μν = p_o(4U^μU^ν/c² - η^μν), because Tr[T_radiation^μν] = (0), which gives {p_o = ρ_eo/3}
T_EM^μν = (1/μ_o)(F^μαη_αβF^νβ - η^μνF_δγF^δγ/4)
T_null-dust^μν = kN^μN^ν{where N is the 4-Null and k is an intensity factor}
Tr[T_perfectfluid^μν] = (ρ_eo - 3p_o)
Tr[T_dust^μν] = (ρ_eo): ie. {p_o = 0}
Tr[T_vacuum^μν] = (4ρ_eo): ie. {p_o = -ρ_eo}
Tr[T_radiation^μν] = (0): ie. {p_o = ρ_eo/3}
Tr[T_EM^μν] = (0)
Tr[T_null-dust^μν] = (0)
Special subcases of the Stress-Energy Tensor can be understood as simple Lorentz Invariant conditions upon which all observers must agree.
They are based on the Trace operator Tr[] = η_μν, which is just the Minkowski Metric
=============================

∂[X] = η^μν
∂·X = 4 = Divergence of SpaceTime
∂·∂[X·X] = ∂·∂[(cτ)²] = 8
U·U = (c)²
P·P = (m_oc)²
∂·F^αν = (μ_o)J
U·F^αν = (1/q)F
J = (q)N
Q = (q)A_EM
J = (ρ_o/m_o)P = (qn_o/m_o)P
P = (E_o/ω_o)K
Tr[ ^μν] = η_μν
Tr[V^μν] = 1 = Tr[Temporal Projection]
Tr[H^μν] = 3 = Tr[Spatial Projection]
Tr[η^μν] = 4 = Tr[SpaceTime Projection]
Tr[N^μν] = 0 = Tr[Null Projection]
Tr[T_perfectfluid^μν] = η_μνT_perfectfluid^μν = ( ρ_eo - 3p_o )
V_μν[T_perfectfluid^μν] = ( ρ_eo )
H_μν[T_perfectfluid^μν] = ( - 3p_o )
Tr[F^μν] = η_μνF^μν = 0
F^μνF_μν = F^μνη_μαη_νβF^αβ = 2(b·b - e·e/c²)
Det[F^μν] = Pf[F^μν]² = {(e·b)/c}²
Tr[M^μν] = η_μνM^μν = 0
δ⁽⁴⁾[X] = 1/(2π)⁴∫d⁴K e^-i(K·X)
Important Physical/Mathematical constants can be found in the 4-Vector Relations.
Universally Constant for All: ( π, η_μν, c, μ_o, ε_o, k_B,"one more really simple important one hint hint", etc.)
Constant which depends on particle-type/setup: ( q, E_o, m_o, ω_o, ρ_eo, p_o, (b·b - e·e/c²), {(e·b)/c}²), S_ent, ...).
In other words, m_o → m_oe, for electron; m_o → m_om for muon; q → q_e for electron; q → q_u = 2/3q_e for up-quark; q → q_d = -1/3q_e for down-quark;

Interestingly,
U·U = c²
E_o/m_o = E/m = c²
(1/ε_oμ_o) = c²
|u * v_phase| = |v_group* v_phase| = c²
The fundamental constant (c) appears in temporal speed, connection of Energy to Mass, the EM field, and particle-wave duality.
=============================

d⁴X = -(V_o)dT·dX = cdt d³x = cdt dx dy dz
d⁴P = (V_Po)dT·dP = (dE/c) d³p = (dE/c) dp_xdp_ydp_z
d⁴K = (V_Ko)dT·dK = (dω/c) d³k = (dω/c) dk_xdk_ydk_z
d³p d³x = (V_Po)dT·(-V_o)dT = ( -V_o V_Po)dT·dT
d³k d³x = (V_Ko)dT·(-V_o)dT = ( -V_o V_Ko)dT·dT
δ⁽⁴⁾[X - X'] = 1/(2π)⁴∫d⁴Ke^{-i(K·(X-X'))} = δ[ct-ct']δ⁽³⁾[x - x'] = δ[ct-ct']δ[x-x']δ[y-y']δ[z-z']
∫_{[Some 4D Volume]}δ⁽⁴⁾[X - X']d⁴X = {1 if X'in the 4D Volume, 0 otherwise}
(∂·∂)G[X - X'] = δ⁽⁴⁾[X-X']
Several calculus results can be extended in 4D, and are shown to be Lorentz Scalar Invariants
=============================

=====================================================================
*********************************************************************
=====================================================================

Ok, up to this point, all of the relations are pretty much straight-forward, no doubts, pure SR.
Each of the 4-Vectors has been used in a classical SR (non-quantum) way.
The versatility of the SR Lorentz Scalar Product, and of the SR 4-Gradient are very apparent.
The use of the 4-Gradient as a 4-Divergence is powerful.
The connection to Classical EM Theory is apparent.
The main point: All of the 4-Vectors come purely from SR theory - No Quantum Assumptions.

The next couple of relations (just two in fact) will be somewhat controversial if one is stuck in the old paradigm of QM as a separate system from SR.
However, I will present evidence that these relations are also purely from SR, and supported by empirical observation.
A few of the empirical effects are:
Planck's Law of Black-Body Radiation
PhotoElectric Effect,
Matter-Wave Effect,
Compton Effect,
Aharonov-Bohm Effect,
Josephson Effect.

=====================================================================
*********************************************************************
=====================================================================

P = ћK
This is the SR 4-Vector version of the Planck-Einstein relation and de Broglie Matter-Wave relation.
One could argue that this is a quantum axiom. However, in this case, it is not.
It is derivable from the SR relations P = m_oU = (E_o/c²)U and K = (ω_o/c²)U
4-Momentum P = (E/c,p) = (mc,p)
4-WaveVector K = (ω/c,k)
4-Velocity U = U^μ = (U⁰,Uⁱ) = γ(c,u)
Since both P and K are Lorentz Scalar proportional to U, then by the mathematics of tensors P must be Lorentz Scalar proportional to K.
(i.e. Tensors obey mathematical transitivity, or in this case they are also Right Euclidean {if a~c and b~c, then a~b} )
P = m_oU = (E_o/c²)U = (E_o/c²)/(ω_o/c²)K = (E_o/ω_o)K = (γE_o/γω_o)K = (E/ω)K = (ћ)K
This is the relation that I have been hinting at in all of the above...
Now, technically, all SR tells us is that there is a invariant Lorentz Scalar with dimensional unit of [action] between these 4-Vectors.
It does not give a value. That comes from experiment.
It is an empirical observation that (E_o/ω_o) = (E/ω) = (ћ) for all known particle types and situations.
However, that is also the case with the Lorentz Scalar speed-of-light (c). SR says there is a invariant Lorentz Scalar with dimensional unit of [velocity], but the value must be empirically measured.
Now then, if one is worried that for photons (E_o/ω_o) = (0/0) = undefined... use the 4-Null N instead.
P = (E/c,p) = (|p|)N = (|p|)(1,n̂) and K = (ω/c,k) = (|k|)N = (|k|)(1,n̂)
where the "intensity" constants are both non-zero for photonic particles.
Thus, P = ((E/c)/(ω/c))K = (E/ω)K = (|p|/|k|)K and again by empirical observation, P = (ћ)K
The constant with dimensional unit [action] turns out to be (ћ = h/2π), with (h) as Planck's constant, can be empirically measured via classical (non-QM) physics knowledge.
This relation is fundamentally no different from the SR P = (m_o/ρ_o)J relation or the SR J = (ρ_o/n_o)N_f = (q)N_f (4-NumberFlux N_f, not 4-Null N) relation which we derived earlier; the method is the same.
Experiments to measure (ћ) include:
Threshold Voltages of LED's, ring radii of Electron Crystal Diffraction, the energy/momentum of Photo-Electrons, the Watt Balance, the Duane-Hunt Law, etc.

For the LED experiment, one uses several different LED's, each with its own characteristic wavelength.
One then makes a chart of wavelength (λ) vs. threshold voltage (V) needed to make each LED emit,
noting that they are proportional via an unknown constant.
One finds that { λ = h*c/(eV) }, with e = ElectronCharge and c = LightSpeed.
h is found by measuring the slope. Consider this as a blackbox for which no assumption about QM is made.
However, we know that E = eV, and λf = c for photons.
The data force one to conclude that E = hf = ћω.
Applying our 4-Vector knowledge, this means that P = (E/c,p) = ћK = ћ(ω/c,k),
because the temporal equation forces the spatial equation to be true as well due to SR mathematics. Thus P = ћK

For the Crystal Diffraction experiment, one measures the diffraction ring radii at various accelerating voltages of the electron beam and for different substances.
One can plot the momentum of the electron beam vs. inverse crystal Bragg wavelength or vice-versa.
One finds that { λ = h/p }.
The momentum (p) of the electron beam is given by { p = √[2m_oeV] }, where (m_o) is the electron mass, (e) is the electron charge, (V) is the Voltage potential.
The crystal Bragg wavelength is given by { λ = 2d sin[θ]/n }, where (d) is a crystal structure constant, (θ) is the angle to the ring, (n) is an integer denoting which ring maximum.
The data force one to conclude that p = h/λ = hk/2π = ћk. In 3D, this is p = ћk.
Applying our 4-Vector knowledge, this means that P = (E/c,p) = ћK = ћ(ω/c,k),
because the spatial equation forces the temporal equation to be true as well due to SR mathematics. Thus P = ћK

For the PhotoElectric experiment, one measures the stopping voltages required for light of various frequencies on different substances.
A photoelectric cell is a device where light shines upon a metallic surface (cathode) and excites the electrons that will be collected by a another metallic surface (anode),
If you connect the cathode and anode through an external circuit, you can measure the current created.
In a more generic sense, the maximum kinetic energy of the electron current is determined by applying a stopping potential between the cathode and the anode to prevent electrons from reaching the anode.
This way, when current no longer flows, we will know the value of the current.
We begin by applying a voltage to the cell.
With the cell in series with the capacitor, the latter will charge as electrons are generated in the cell.
This creates an electric current through the cell.
As the capacitor charges, the voltage between its terminals increases, reducing the voltage between the terminals of the cell (because Vbat=Vcap+Vcell=constant).
When the cell voltage reaches a certain value, the stopping voltage, current no longer flows and the capacitor maintains a constant voltage.
These results are plotted on a graph producing a line. One uses a linear regression on the line to get a slope and y-intercept.
One finds that the slope is equal to some constant / e, and the y-intercept gives a constant which depends on the substance.
Writing this out one has voltage V = (slope constant / e)*light frequency - the substance constant.
The slope constant is h. The substance constant is a work function W_o.
Multiplying everything by e one gets maxKE = eV = hf - eW_o.
One finds that the Energy of the incoming light E = hf = ћω
etc. etc.

For the Watt Balance experiment, one eventually gets { h = 4/(K_J²R_K) } where:
The Josephson Constant { K_J = 2e/h = 1/(MagneticFluxQuantum) }, measured via the Josephson Effect { U_J[n] = nf/K_J}
The von Klitzing Constant { R_K = h/e²}, measured via the Quantum-Hall Effect {R_H[i] = R_K/i}

Historically:
Planck discovered (h) based on statistical-mechanics/thermodynamic considerations of the black-body problem in 1900.
Einstein applied Planck's idea to photons in the Photoelectric Effect to give ( E = ћω ) in 1905.
de Broglie realized that every particle, massive or massless, has 3-vector momentum ( p = ћk ) in 1924.
Putting it all together naturally produces the SR 4-Vector relation P = ћK.
P = (E/c,p) = ћK = ћ(ω/c,k)
Thus the Matter-Wave Effect was established.

This also gives Action S_act = ћΦ_T with:
S_act = -(P_T·R) = - ћ(K_T·R)
S_act = -∫(P_T·dR) = -∫(P_T·dR/dτ)dτ = -∫(P_T·U)dτ = -∫(P_T·U/γ) dt = ∫L dt
S_act = -∫(P_T·dR) = - ћ∫(K_T·dR)
where the subscript (_T) indicates that is it referring to the "Total" or "Canonical" values.
=============================

∂ = -iK {for f = ae^-i(K·X)}
The SR Plane-Wave Equation... among other things...
Up to this point, we have noticed that the various SR 4-Vectors have been related to one another by simple Lorentz Scalar constants.
Now, let's do a mathematical experiment, let's see if the 4-Gradient can be related to the other SR 4-Vectors with a simple Lorentz Scalar.
Which 4-Vector might it be related to? Well, both ∂ and K have dimensional units of [length^-1].
Also, we showed earlier that { K = -∂[Φ] }, i.e. the 4-WaveVector is defined by the negative 4-Gradient of the SR Phase.
Let's take this a bit further.
Let { f = f [Φ] } be some arbitrary function (f [ ]) of the SR Phase Φ.
Then ∂[f] = f ' ∂[Φ] = f ' (-K) = (-K) f '
Is there a general function ( f ) that solves this?
Try { f(Φ) = ae^i(Φ) }, a plane wave equation which gives { f ' = i f }
∂[f] = (i)ae^i(Φ)∂[Φ] = (i)ae^i(Φ)(-K) = (-iK)ae^i(Φ) = (-iK)f
∂[f] = (-iK)f
∂ = -iK {for f = ae^i(Φ), and this is manifestly Lorentz Invariant}

Now, showing the same argument slightly differently...
K·X = (ω/c,k)·(ct,x) = (ωt - k·x) = -Φ
Construct {f = ae^b(K·X) = ae^b(-Φ)}, which is just a simple exponential function of 4-Vectors, specifically the SR Phase Φ in this case...
Then ∂[f] = ∂[ae^b(K·X)] = (bK)ae^b(K·X) = (b K)f
And ∂·∂[f] = b²(K·K)f = (bω_o/c)²f
Note that { b = ±i } is an interesting choice → it leads to SR Plane Waves, which we observe empirically, eg. EM Plane Waves = Photons...
Also, since K is the 4-WaveVector, this is a totally reasonable choice.
Typically, { b = -i } is chosen.
This gives:
∂[f] = (-iK)ae^-i(K·X)
∂[f] = (-iK)f
∂ = -iK{for f = ae^-i(K·X), and this is manifestly Lorentz Invariant}
This is nice because the (-i) ends up being a Lorentz Scalar invariant between the two 4-Vectors, ∂ and K.
This is the same thing that was used in the relativistic description of the 4-WaveVector
The relativistic condition { K = -∂[Φ]} is that which chooses { ∂ = -iK for f = ae^i(Φ)}

Now, observing a little more closely:
∂·∂[f] = b²(K·K)f = (bω_o/c)²f
{ b = ±i } either choice gives plane waves
∂[f] = (±iK)ae^±i(K·X) = ±iKf
∂ = ±iK
∂_X = ±iK
There are actually two possible choices...

*Further note*
The character of the constant (a) is not specified.
(a) could be a Lorentz Scalar, a 4-Vector, a higher-order tensor, etc.
We saw this in the SR wave chart, where you could have scalar waves (Lorentz Scalar a), Photonic waves (4-Vector a), Graviatational waves (Rank-2 Tensor a).

==============================

Now, let us see what takes the purely SR 4-Vectors into the quantum arena...

The "Quantum Stuff" is marked in Orange/Black - "Spooky action at a distance", lol ;)

=====================================================================
*********************************************************************
=====================================================================

That's it, just those few incredibly simple SR relations, putting new constants on physical objects already connected in standard SR,
and the recognition that:
the 4-ProbabilityCurrentDensity is formally equivalent to the 4-NumberFlux we met when dealing with SR Fluids and SR Dust...
the 4-Spin of QM particles is just like the 4-Polarization that occurs in purely SR electromagnetic waves.
See the Jones Vector and classical EM photon polarization.

What are the consequences of ∂ = -iK {for f = ae^-i(K·X)}?

Answer: We just derived Quantum Mechanics (QM) from Special Relativity (SR) + a few empirical observations.
This is the SRQM Interpretation, or alternately, the [SR→QM] Interpretation.
We did NOT assume any Quantum Axioms. Essentially, we are simply allowing complex numbers...
See below...

Why was this simple connection not noticed before?
Why were 4-Vectors not used previously to see this connection?
There were some famously brilliant physicists and mathematicians looking at this, how did they miss it?

Answer: The pioneers of SR and QM did not have the power of the 4-Vector formalism at the start.
Einstein's PhotoElectric Effect, giving ( E = ћω ) was explained in 1905.
Using SR 4-Vector formalism, this immediately gives ( P = ћK ) as a 4-Vector relation. That's the way SpaceTime works.
However, the spatial component of this equation was not noticed/understood until de Broglie gave his "Matter Wave Hypotreatise" and ( p = ћk ) in 1924,
almost a full 20 years later! And even then, he referred to it as "a hypotreatise".

Schrödinger gave his QM relations even later, formulated late in 1925 and published in 1926.
In standard QM, we jump directly to ( E = iћ∂_t ), which is given the status of a quantum postulate,
again not emphasizing that this is just the temporal component of P = (E/c,p) = iћ∂ = iћ(∂_t/c,-∇),
and not giving much heed that this is actually made of two separate assumptions: ( P = ћK ) and ( K = i∂ )
Minkowski had noticed the connection between Einstein's SR and his own 4D Minkowski SpaceTime in 1907.
However, it still took decades before the formalism of Physical SR 4-Vectors caught on.

Another point that obscured things, was notational.
In GR, the 4-Gradient (∂) is quite often written in "comma form" as ( , ).
For example, the Faraday Tensor ( F_μν = ∂_μA_ν - ∂_νA_μ ) is often written as ( F_μν = A_ν,μ - A_μ,ν ).
This notation, while succinct, obscures all the power of the 4-Gradient that we just discovered in all the relations above on the webpage.
Who has ever seen or written the Schrödinger relations as (P_μ = iћ_,μ )? I don't think I ever saw it as such elsewhere.
The comma notation, while great for GR stuff, obscures it's relation to QM stuff.

Another point is the prevailing paradigm that SR and QM are "separate" things.
Once I had researched 4-Vectors for awhile, I showed it to my old GA Tech Physics Professor and thesis advisor, David Finkelstein.
Even when I showed him that the 4-Vector formalism shows a non-zero commutation relation in SR, he refused to accept it.
I showed him the math, and asked him to point out the error. He could never show the math wrong, but he still refused to accept it.
He stuck adamantly to rote that: "Position and momentum do not have a non-zero commutation relation in SR".
David for years was searching of the "most basic and fundamental" forms of QM, from which he could build SpaceTime.
Every week at his lectures he would have new "fundamental" object, but none could ever seem to "Quantize SpaceTime" the way he wanted.
I don't think he ever considered approaching the problem from the SR side.
When I showed him the 4-Velocity, and the 4-UnitTemporal, he dismissed them out of hand,
again by rote arguing that SR objects could not lead to QM.

However, one thing David always said was to be bold in searching for the answers in Physics,
Well, see below...

=====================================================================
*********************************************************************
=====================================================================

SRQM 4-Vector : Four-Vector SR Quantum RoadMap

SRQM 4-Vector : Four-Vector SR Quantum RoadMap

Quantum Mechanics from SR 4-Vector Relations

What are usually known as QM Axioms are instead SR derived Principles of QM...
Ok, so for all the relations above, everything was found via pure mathematics or via empirical experimentation.
They are all manifestly covariant, not to mention extremely simple - Many of the 4-Vectors are simple Lorentz scalar proportional to one another.
In no case is knowledge of QM or QM axioms required, the values of the Lorentz scalars are determined empirically.
Form a chain of properties, where each new 4-Vector is related to the last one:
R = (ct,r)
U = (d/dτ)R
P = (m_o)U
K = (1/ћ)P
∂ = (-i)K

The Relativistic Klein-Gordon Quantum Wave Equation, and other RWE's :
Form a chain of Lorentz Scalar Equations...
U·U = (c)²
P·P = (m_oc)²
K·K = (m_oc/ћ)² = (ω_o/c)²
∂·∂ = (-im_oc/ћ)² = -(m_oc/ћ)² = -(ω_o/c)²
The last is a fundamental quantum relation.
When applied to a Lorentz Scalar, it gives the free particle Klein-Gordon Equation (the Relativistic Quantum Wave Equation for Spin-0 Particles).
[ (∂·∂) + (m_oc/ћ)² ]ψ(X^μ) = 0
When applied to a 4-Vector, it gives the free particle Proca equation (massive case m_o > 0), and the free Maxwell equation (massless case m_o = 0)
The Schrödinger Equation, and hence Quantum Mechanics, is just the low-velocity (|v| << c) limiting-case of the KGE.
This is (RQM) = Relativistic Quantum Mechanics, derived from only:
It is interesting to note that one can do the KG Equation with just a rest frequency (ω_o) and the speed of light (c).
Planck's constant (h) is not actually required, even though it is an empirical fact.
The more commonly seen Schrödinger Quantum Wave Equation is just the low velocity limit { |v| << c } of the Klein-Gordon Equation,
in exactly the same way the Classical Dynamics is the low velocity limit { |v| << c } of SR Dynamics.
=============================

Operator Formalism : [∂] = -iK
Unitary Evolution : ∂ = [-i]K
Wave Structure : ∂ = -i[K]
These three are straight from the basic mathematical equation for plane waves.
1st, the 4-Gradient is already an operator in SR. We showed many, many ways that it is used in SR. We don't need an extra QM axiom for it.
2nd, the wave here evolves unitarily - it's a plane wave. We observe plane waves empirically in photon phenomena. ∂ = -iK {for f = ae^-i(K·X)}
3rd, it's a particle, but it's also a wave. The 4-WaveVector is a standard SR 4-Vector, as the SR Doppler Effect indicates.

I want to comment a little here.
One of the main differences between classical and quantum variables is that the quantum variables are "operators".
However, it can be clearly demonstrated that pretty much all "operator" variables can be related back to the SR 4-Gradient,
which was an operator/function before ever mentioning anything quantum.
Even the position can be related back to an SR 4-WaveGradient, which is already an operator/function.
Operators are not from QM axioms, they come from simple SR 4-Vector Gradient functions.

From Wikipedia Photon Polarization: "Much of the mathematical machinery of quantum mechanics, such as state vectors, probability amplitudes, unitary operators, and Hermitian operators, emerge naturally from the classical Maxwell's equations in the description. The quantum polarization state vector for the photon, for instance, is identical with the Jones vector, usually used to des cribe the polarization of a classical wave. Unitary operators emerge from the classical requirement of the conservation of energy of a classical wave propagating through lossless media that alter the polarization state of the wave. Hermitian operators then follow for infinitesimal transformations of a classical polarization state. Many of the implications of the mathematical machinery are easily verified experimentally. In fact, many of the experiments can be performed with two pairs (or one broken pair) of polaroid sunglasses"

Scalar Wave functions are Lorentz Scalar Invariant, which can have complex values.
ψ'[X^μ'] = ψ'[Λ^μ'_νX^ν] = ψ[X^μ]
Function values of the wave function in the new frame are identical to the function values of the wave function in the old frame {taken at the same SpaceTime point}.

∂ = -iK is a Correspondence Principle which allows classical obsevables to be represented by quantum operators.
=============================

The Schrödinger QM Relations :
P = ћK
K = i∂
combined give
P = iћ∂
Thus P = (E/c,p) = iћ∂ = iћ(∂_t/c,-∇).
The temporal eqn. is { E = iћ∂_t}, the Schrödinger QM Energy Relation.
The spatial eqn. is { p = -iћ∇}, the Schrödinger QM 3-momentum Relations.
These were generated by the SR Lorentz scalar product relations between the physical SR 4-Vectors {P,K,∂}
P = ћK is required to exist since both P and K are Lorentz scalar proportional to U,
and is the 4D encapsulation of the Planck-Einstein photon relation and de Broglie Matter-Wave relation.
K = i∂ is just the noticing of particle plane waves, for both photons and massive particles.
This is really nice because when I first saw { E = iћ∂_t} and { p = -iћ∇} as an undergrad physics major,
I thought the equations very mysterious, like where the heck does that come from?
They were simply presented as a postulate of QM. You had to just accept it.
Now, by breaking it into separate steps using SR, it makes sooooo much more sense...

Now, there are some details that math purists would want to address, such as for strict equality the 4-Momemtum P should be "promoted" to a 4-MomentumOperator P̂.
Once you get into Hilbert space descriptions, you get at least 3 (slightly?/greatly?) different aspects of the same thing.
P̂| P ⟩ = P| P ⟩.
The 4-MomentumOperator P̂ acts on the 4-MomentumState | P ⟩ to give a numerical value 4-Momentum P.
However, if we treat this in an abstract symbolic way, the math all works out the same.
P̂ = ћK̂
P = ћK
| P ⟩ = ћ| K ⟩
Whatever the differences are, they all symbolically follow the same relativistic laws.
=============================

SRQM 4-Vector : Four-Vector Quantum Canonical Commutation Relation

SRQM 4-Vector Quantum Canonical Commutation Relation

Non-zero Commutation Relation between position and momentum :
4-Position X = (ct,x)
4-Gradient ∂ = (∂_t/c,-∇)
4-Momentum P = (E/c,p)
Let { f } be an arbitrary SR function.
X[f] = Xf
∂[f] = ∂[f]
X[∂[f]] = X∂[f]
∂[X[f]] = ∂[Xf] = ∂[X]f + X∂[f]
∂[Xf] - X∂[f] = ∂[X]f
∂[X[f]] - X[∂[f]] = ∂[X]f

Now with commutator notation...
[∂,X]f = ∂[X]f

And since f was an arbitrary SR function, we can remove it, which leaves...
[∂,X] = ∂[X] = (∂_t/c,-∇)[(ct,r)] = (∂_t/c,-∂_x,-∂_y,-∂_z)[(ct,x,y,z)] = Diag[+1,-1,-1,-1] = η^μν = Minkowski Metric
[∂^μ,X^ν] = ∂^μ[X^ν] = η^μν = Minkowski Metric

hence
[∂,X] = [∂^μ,X^ν] = η^μν = Minkowski Metric, and thus inherently a non-zero commutation relation
====
At this point, we have established purely mathematically, that there is a non-zero commutation relation between the SR 4-Gradient and SR 4-Position
Note also that { X[f] = Xf } doesn't actually say that X is an operator.
It just says that {an X next to an f} = {X next to f}.
It could be an operator or just a number.
We know for a fact that ∂ is an operator, because it is already an operator in pure SR.

Now, using { ∂ = -iK and P = ћK }, which we derived from above...
[∂,X] = [∂^μ,X^ν] = η^μν
[K,X] = [K^μ,X^ν] = iη^μν
[P,X] = [P^μ,X^ν] = iћη^μν

[X^μ,P^ν] = - iћη^μν and, looking at just the spatial part...

[x^j,p^k] = iћδ^jk

see Canonical Commutation Relation, Commutator, Poisson Bracket, Stone-von Neumann Theorem,
***************************************************************************

Hence, we have derived the standard QM commutator rather than assume it as an axiom...
This makes way more sense than the standard argument, which reverses the logical derivation.
In other words, [x^j, p^k] = iћδ^jk is pretty much assumed as an axiom of quantum theory,
then it is used to justify p = -iћ∇
I was never convinced by this standard argument when I was in grad school back in the day.
It felt too much like creating something from thin air.

***************************************************************************

The non-zero commutation is *NOT* about the size of (ћ) or the imaginary (i).
The source is the Minkowski Metric η^μν, which gives non-zero commutation relations between the SR 4-Gradient and SR 4-Position.
The closest classical form of this is the Poisson Bracket.

Note that we also have:
[X⁰,P⁰] = - iћη⁰⁰
[ct,E/c] = [t,E] = -iћ
[E,t] = iћ
Thus the much debated time-energy uncertainty relation is very simple from the SR point of view.
see Heisenberg uncertainly relation,
====

Going back to the original argument, this time using a function of 4-Position
Let f be an arbitrary SR function, and let g = SR function of 4-Position = g(X).
g(X)[f] = g(X)f
∂[f] = ∂[f]
g(X)[∂[f]] = g(X)∂[f]
∂[g(X)[f]] = ∂[g(X)f] = ∂[g(X)]f + g(X)∂[f]
∂[g(X)f] - g(X)∂[f] = ∂[g(X)]f

Now with commutator notation...
[∂,g(X)]f = ∂[g(X)]f

And since f was an arbitrary SR function...
[∂,g(X)] = ∂[g(X)] = g'(X)∂[X] = g'(X)η^uv
The usual commutation results using a function of position...

[∂,g(X)] = ∂[g(X)] = g'(X)∂[X] = g'(X)η^uv
Now, let's look at just the temporal part of the 4-Gradient:
[∂⁰,g⁰(X)] = [∂_t/c,g_t(X)] = (1/c)g_t'(X)(η⁰⁰) = (1/c)g_t'(X)(1) = (1/c)g_t'(X)
[∂_t/c,g_t(X)] = (1/c)g_t'(X)
[∂_t,g_t(X)] = g_t'(X)
(iћ/iћ)[∂_t,g_t(X)] = g_t'(X)
(1/iћ)[iћ∂_t,g_t(X)] = g_t'(X)
(1/iћ)[E,g_t(X)] = g_t'(X)
(1/iћ)[H,g_t(X)] = g_t'(X)
(-i/ћ)[H,g_t(X)] = g_t'(X)
(-i/ћ)[H,g_t(X)] = g_t'(X)
(i/ћ)[g_t(X),H] = g_t'(X)
(i/ћ)[Q,H] = Q̇ : missing a minus sign and not valid for Heisenberg operators
Heisenberg Picture,

====
We can also try [P^μ, P^ν], where P_T^μ = P^μ + A^μ and [P_T^μ, P_T^ν] = 0 (ie. the Canonical or Total 4-Momentum commutes)
*** I might have this backwards, and the dynamical 4-Momentum commutes; need to double-check ***

[P^μ, P^ν] =
= [P_T^μ - qA^μ, P_T^ν - qA^ν]
= [P_T^μ, P_T^ν] + [P_T^μ, -qA^ν] + [-qA^μ, P_T^ν] + [-qA^μ, -qA^ν]
= 0 + q[P_T^μ, -A^ν] + q[-A^μ, P_T^ν] + 0
= q[P_T^μ, -A^ν] + q[-A^μ, P_T^ν]
= -q([P_T^μ, A^ν] + [A^μ, P_T^ν])
= -q([P^μ + A^μ, A^ν] + [A^μ, P^ν + A^ν])
= -q([P^μ, A^ν] + [A^μ, A^ν] + [A^μ, P^ν] + [A^μ,A^ν])
= -q([P^μ, A^ν] + (0) + [A^μ, P^ν] + (0))
= -q([P^μ, A^ν] + [A^μ, P^ν])
= -iћq([∂^μ, A^ν] + [A^μ, ∂^ν])
= -iћq(∂^μA^ν - ∂^νA^μ)
= -iћq(F^μν)

[P_T^μ, P_T^ν] = 0 and [P^μ, P^ν] = -iћq(F^μν)

[p^j, p^k] = -iћq(F^jk) = -iћq(-ε_jklb^l) = iћq(ε_jklb^l) = orthogonal momenta affected by right-hand-rule magnetic field (b^l)

see Canonical Commutation Relation in EM potential, Landau Quantization, Zeeman Effect, QED Vacuum, Quantization of the EM Field,
This would also give...
[p⁰, p^k] = -iћq(F^0k) = -iћq(-e^k/c) = iћq(e^k/c)
[E/c, p^k] = iћq(e^k/c)
[E, p^k] = iћq(e^k) = Energy|momentum affected by electric field (e^k)

using
F^μν = (∂^μA_EM^ν - ∂^νA_EM^μ)
=

0	-e^x/c	-e^y/c	-e^z/c
e^x/c	0	-b^z	b^y
e^y/c	b^z	0	-b^x
e^z/c	-b^y	b^x	0

0	-eⁱ/c
+e^j/c	-ε_ijkb^k

[P^μ, P^ν] = -iћq(F^μν) = [m_oU^μ, m_oU^ν]
[m_oU^μ, m_oU^ν] = -iћq(F^μν)
m_o²[U^μ, U^ν] = -iћq(F^μν)
[U^μ, U^ν] = (-iћq/m_o²)(F^μν)

[γ_ju^j, γ_ku^k] = (-iћq/m_o²)(F^jk)
γ_jγ_k[u^j, u^k] = (-iћq/m_o²)(F^jk)
[u^j, u^k] = (-iћq/γ_jγ_km_o²)(F^jk)
[u^j, u^k] = (-iћq/γ_jγ_km_o²)(-ε_jklb^l)
[u^j, u^k] = (iћq/γ_jγ_km_o²)(ε_jklb^l)
====

We can actually continue this using the Wave-space or Momentum-space representation

4-WaveVector K = (ω/c,k)
4-Gradient ∂ = ∂_X = (∂_t/c,-∇_x)
4-WaveGradient ∂_K = (c∂_ω,-∇_k)
4-MomentumGradient ∂_P = (c∂_E,-∇_p)
Let f be an arbitrary SR function.
K[f] = Kf
∂_K[f] = ∂_K[f]
K[∂_K[f]] = K∂_K[f]
∂_K[K[f]] = ∂_K[Kf] = ∂_K[K]f + K∂_K[f]
∂_K[Kf] - K∂_K[f] = ∂_K[K]f

Now with commutator notation...
[∂_K,K]f = ∂_K[K]f

And since f was an arbitrary SR function...
[∂_K,K] = ∂_K[K] = (c∂_ω,-∇_k)[(ω/c,k)] = (c∂_ω,-∂_kx,-∂_ky,-∂_kz)[(ω/c,k_x,k_y,k_z)] = Diag[+1,-1,-1,-1] = η^μν = Minkowski Metric

hence
[∂_K,K] = [∂_K^μ,K^ν] = η^μν = Minkowski Metric
Once again, the non-zero commutation is due to the Minkowski Metric, not Planck's constant (ћ), not the imaginary unit (i)
====
Now then, we arbitrary chose (-i) from the SR phase definition of plane waves: ∂ = -iK
or, to be careful here, distinguishing the 4-PositionGradient ∂_Xvs. the 4-WaveVectorGradient ∂_K, ∂_X = -iK

But, the equation needs to work for both the (+) and (-) definition:

∂_X = ±iK

[∂_X,X] = η^μν = [∂_K,K]
[∂_X,X] = [∂_K,K]
[∂_X,X] = -[K,∂_K]
[±iK,X] = -[K,∂_K]
±i[K,X] = -[K,∂_K]
±i²[K,X] = -i[K,∂_K]
±(-1)[K,X] = -i[K,∂_K]
±[K,X] = i[K,∂_K]
[K,X] = ±i[K,∂_K]
[K,X] = [K,±i∂_K]

X = ±i∂_K
∂_K = ∓iX

We see that the Fourier Transform correctly pops out automatically, creating automatic duality.
∂_X = (±i)K
∂_K = (∓i)X

We again temporarily chose the standard convention (K = i∂)
And continuing to momentum-space (P = ћK,∂_K = ћ∂_P)
X = -i∂_K = -iћ∂_P

P = (E/c,p) = iћ∂_X = iћ(∂_t/c,-∇_x) = iћ(∂_t/c,-∇_x) giving ( E = iћ∂_t and p = -iћ∇_x ) in the Position-Space Representation
X = (ct,x) = -iћ∂_P = -iћ( c∂_E,-∇_p) = iћ(-c∂_E,∇_k) giving ( t = -iћ∂_E and x = iћ∇_p ) in the Momentum-Space Representation

Note: Given that we started with the SR SpaceTime formulation, there is no valid reason to discount the ( t = -iћ∂_E ) formula.
Space and time are on an equal footing in SR. It is just as valid as the other 3 formulas.

Those derivations that do discount (t = -iћ∂_E) as a valid statement started with classical assumptions, not relativistic, which is incorrect thinking:
(i.e. Relativistic is *NOT* the generalization of Classical/Newtonian,
Classical/Newtonian is the limiting-case approximation of Relativistic for |v| << c )

So, the Lorentz Scalar (i) is the physical "thing" connecting particles to waves, since it is this relation that gives the Fourier Transforms and wave relations.
(ћ) is more a connection between the light-cone boundary (massless photonic behavior) and the light-cone interior (massive particle behavior).

Again
[∂,X] = η^μν = Minkowski Metric
[P,X] = iћη^μν
We will find later that the Dirac Gamma's have an anti-commutation relation
{Γ^μ,Γ^ν} = 2 η^μν I₄;Note this is also related to SpaceTime Algebra
where I₄ is the 4x4 Identity Matrix, Γ^μ = (γ⁰,γ) and Γ_μ = η_μνΓ^ν = (γ⁰,-γ)
The Dirac RQM Equation
iћ(Γ^μ∂_μ)Ψ = (m_oc)Ψ

We also get commutation relations for the Relativistic Angular momentum:
Relativistic Angular Momentum (Pseudo-)Tensor M^μν = (X^μP^ν - X^νP^μ) = 2(X^[μP^ν]) = {sometimes written as L^μν}
M^μν = (X^μP^ν - X^νP^μ) = iћ(X^μ∂^ν - X^ν∂^μ)
[M^μν, M^ρσ] = iћ(η^νρM^μσ + η^μσM^νρ + η^σνM^ρμ + η^ρμM^σν)
[M^μν, P^ρ] = iћ(η^ρνP^μ - η^ρμP^ν)

Once more, note that the "operator" part of the this is actually coming from the 4-Gradient.
=============================

Heisenberg Uncertainty :
The core of the Heisenberg Uncertainty Equation comes from the non-zero commutator, which was proved above.
The Generalized Uncertainty Relation: σ_f²σ_g² = (ΔF) * (ΔG) >= (1/2)|⟨ i[F,G] ⟩|
The uncertainty relation is a very general mathematical property, which applies to both classical or quantum systems.
From Wikipedia: Photon Polarization:
"This is a purely mathematical result. No reference to a physical quantity or principle is required."

The Cauchy–Schwarz inequality asserts that (for all vectors f and g of an inner product space, with either real or complex numbers):
σ_f²σ_g² = [⟨ f | f ⟩·⟨ g | g ⟩] >= |⟨ f | g ⟩|²

But first, let's back up a bit; Using standard complex number math, we have:
z = a + ib
z* = a - ib
Re(z) = a = (z + z*)/(2)
Im(z) = b = (z - z*)/(2i)
z*z = |z|² = a² + b² = [Re(z)]² + [Im(z)]² = [(z + z*)/(2)]² + [(z - z*)/(2i)]²
or
|z|² = [(z + z*)/(2)]² + [(z - z*)/(2i)]²

Now, generically, based on the rules of a complex inner product space we can arbitrarily assign:
z = ⟨ f | g ⟩, z* = ⟨ g | f ⟩ Which allows us to write:
|⟨ f | g ⟩|² = [(⟨ f | g ⟩ + ⟨ g | f ⟩)/(2)]² + [(⟨ f | g ⟩ - ⟨ g | f ⟩)/(2i)]²
*Note* This is not a QM axiom - This is just pure math. At this stage we already see the hints of commutation and anti-commutation.
It is true generally, whether applying to a physical or purely mathematical situation.

We can also note that:
| f ⟩ = F| Ψ ⟩ and | g ⟩ = G| Ψ ⟩

Thus,
|⟨ f | g ⟩|² = [(⟨ Ψ |F* G| Ψ ⟩ + ⟨ Ψ |G* F| Ψ ⟩)/(2)]² + [(⟨ Ψ |F* G| Ψ ⟩ - ⟨ Ψ |G* F| Ψ ⟩)/(2i)]²

For Hermetian Operators...
F* = +F, G* = +G

For Anti-Hermetian (Skew-Hermetian) Operators...
F* = -F, G* = -G

Assuming that F and G are either both Hermetian, or both anti-Hermetian...

|⟨ f | g ⟩|² = [(⟨ Ψ |(±)FG| Ψ ⟩ + ⟨ Ψ |(±)GF| Ψ ⟩)/(2)]² + [(⟨ Ψ |(±)FG| Ψ ⟩ - ⟨ Ψ |(±)GF| Ψ ⟩)/(2i)]²

|⟨ f | g ⟩|² = [(±)(⟨ Ψ |FG| Ψ ⟩ + ⟨ Ψ |GF| Ψ ⟩)/(2)]² + [(±)(⟨ Ψ |FG| Ψ> - ⟨ Ψ |GF| Ψ ⟩)/(2i)]²

We can write this in commutator and anti-commutator notation...

|⟨ f | g ⟩|² = [(±)(⟨ Ψ |{F,G}| Ψ ⟩)/(2)]² + [(±)(⟨ Ψ |[F,G]| Ψ ⟩)/(2i)]²

Due to the squares, the (±)'s go away, and we can also multiply the commutator by an ( i² )

|⟨ f | g ⟩|² = [(⟨ Ψ |{F,G}| Ψ ⟩)/2]² + [(⟨ Ψ |i[F,G]| Ψ ⟩)/2]²

|⟨ f | g ⟩|² = [(⟨ {F,G} ⟩)/2]² + [(⟨ i[F,G] ⟩)/2]²

The Cauchy–Schwarz inequality again...
σ_f²σ_g² = [⟨ f | f ⟩·⟨ g | g ⟩] >= |⟨ f | g ⟩|² = [(⟨ {F,G} ⟩)/2]² + [(⟨ i[F,G] ⟩)/2]²

Taking the root:
σ_fσ_g >= (1/2)|⟨ i[F,G] ⟩|
Which is what we had for the generalized Uncertainty Relation.

Now for a few comments:
The Uncertainty Principle *IS NOT* about properties, it *IS* about measurements.
The commutator, and hence the Heisenberg Uncertainty Equation, is specifically about "sequential" measurements,
not "simultaneous" measurements and not "simultaneous" properties.
This commutator has to do with the order of the operations acting on an event's worldline, which indicates timelike intervals, not spacelike intervals.
Thus, it makes no statement about whether a given event's "properties" can be simultaneous or not.
It also makes no statement about "simultaneous measurements", other than that certain types of measurements cannot be simultaneous.
It does make a statement about the effects of "sequential measurements" along the timelike intervals of individual worldlines.
The SRQM interpretation is that non-commuting measurements cannot be simultaneous, which makes way more sense than non-commuting properties not being able to be simultaneous.

In other words (and to remove all the hype about properties not existing till measured, etc.):
A particle always has its full set of properties.
A measurement is an arrangement of matter/photons/whatever that interacts with a particle in such a way that information about a particular particle property may be obtained by an observer.
**It is not possible to arrange a configuration of matter that will give simultaneous information about a pair of particle's properties if the measurement arrangement for each are non-commuting.**

Note that the Uncertainty Principle is not a uniquely quantum phenomenon, one can find classical analogs...
Example:
-----------
Consider a coin, a pencil with eraser, a light. The properties of the coin are as follows: heads up/tails up, visible side marked/unmarked, lighted/un-lighted.
Possible operations are: Flip Coin, Mark/Unmark Coin Face, Light On/Off

Example of commuting operations: [Flip Coin, Light Switch] = 0
Start Heads Up & No Light: Then Flip to Tail followed by Light On = Light On followed by Flip to Tail.

Example of non-commuting operations: [Flip Coin, Mark Coin] = / = 0
Start Heads Up & No Mark: Then Flip to Tail followed by Mark Coin Face = / = Mark Coin Face followed by Flip to Tail.

Note that some of these properties are with respect to the observer, following the whole idea of the Relativistic Derivation.
The coin always has each of these binary properties (1 of 2 sides up, face marked or unmarked, face lighted/un-lighted), it is the measurement process that is possibly non-commuting.

Which operation can be simultaneous? Try Light and Flip... These are independent, they commute.
Which operations cannot be simultaneous? Try Mark and Flip... You can't do both at the same time, they are non-commuting.

So, Non-commutativity and Uncertainty are not fundamentally quantum things...
Also, again note that the non-commutativity comes from the operations, the measurements, not the properties.

Let's try another example:
-------------------------------
Consider public-private key cryptography.
For any given person's public-private key pair the following applies:
A message encrypted with the public key can only be decrypted by the private key.
A message encrypted with the private key can only be decrypted by the public key.
To use the system, each person keeps secret thier own private key, but anyone and everyone can have the public key.

Now, consider the following operations between persons A, B, and C:
A encrypts a message with publicB, then encrypts that with privateA, then sends the message to B.
B first has to decrypt with publicA, proving that the message came from A, because only A could have encrypted it with privateA.
However, since everyone has publicA, anyone who intercepts the message knows that it must have come from A.
The original message might be intercepted by person C, who could then send a unsigned spoof message since he has a publicB key also.
B then has to decrypt the message with privateB, which only B can do.
However, B cannot be sure who the message is actually from, so he can't tell if it is legit or not.

Now, consider the if the order had been reversed:
A encrypts a message with privateA, then encrypts that with publicB, then sends the message to B.
B first has to decrypt with privateB, which only B can do, because only B hase a privateB key.
B then has to decrypt with publicA, proving that the message came from A, because only A could have encrypted it with privateA.
Now, A and B have a secure means of communication, since only B can open the outer part, and only A could have sent it.
C is unable to tell who sent the message, and cannot spoof an A message to B since C can't encrypt with privateA.

The message, ie. the particle properties or information, was always there.
The order of the operations, the measurements, made a difference in the final information delivered, whether it was private, whether it was legit.
The main point of this example is that it shows non-commutativity for information.
The message doesn't even have to be a physical thing - just a bunch of symbols.
The measurement process is a way of handling information about a system obtainable by observers.

Let's examine the simultaneous vs. sequential aspect of it:

Consider the following:
Operator A acts on System | Ψ ⟩ at SR Event A: A| Ψ ⟩ →| Ψ' ⟩
Operator B acts on System | Ψ' ⟩ at SR Event B: B| Ψ' ⟩ →| Ψ'' ⟩
or BA| Ψ ⟩ = B| Ψ' ⟩ = | Ψ'' ⟩

If measurement Events A & B are space-like separated, then there are different observers who can see
{A before B, A simultaneous with B, A after B},
which of course does not match the quantum description of how Operators act on Kets

If Events A & B are time-like separated, then all observers will always see A before B. This does match how the
operators act on Kets, and also matches how | Ψ ⟩ would be evolving along its worldline, starting out as| Ψ ⟩,
getting hit with operator A at Event A to become | Ψ' ⟩, then getting hit with operator B at Event B to become| Ψ'' ⟩.

The Uncertainty Relation here does NOT refer to simultaneous (space-like separated) measurements nor simultaneous properties,
it refers to sequential (time-like separated) measurements along individual worldlines.
This removes the need for ideas about the particles not having simultaneous properties.
There are simply no “simultaneous non-commuting measurements” on an individual system, on a single worldline.
They are sequential, and the first measurement places the system in such a state that the outcome of
the second measurement will be altered wrt. if the order of the operations had been reversed.
=============================

Photon Polarization :
Much of the mathematical apparatus of quantum mechanics appears in the classical description of a polarized sinusoidal electromagnetic wave. The Jones vector for a classical wave, for instance, is identical with the quantum polarization state vector for a photon. The right and left circular components of the Jones vector can be interpreted as probability amplitudes of spin states of the photon. Energy conservation requires that the states be transformed with a unitary operation. This implies that infinitesimal transformations are transformed with a Hermitian operator. These conclusions are a natural consequence of the structure of Maxwell's equations for classical waves.
From Wikipedia: Photon Polarization:
"Much of the mathematical machinery of quantum mechanics, such as state vectors, probability amplitudes, unitary operators, and Hermitian operators, emerge naturally from the classical Maxwell's equations in the description.
The quantum polarization state vector for the photon, for instance, is identical with the Jones vector, usually used to describe the polarization of a classical wave.
Unitary operators emerge from the classical requirement of the conservation of energy of a classical wave propagating through lossless media that alter the polarization state of the wave.
Hermitian operators then follow for infinitesimal transformations of a classical polarization state."
→ (0,c_x,c_y,0)
→ (0,1,0,0) = x-polarized
→ (0,0,1,0) = y-polarized (rotated 90°)

for photon travelling in z-direction
using the Jones Vector formalism n = z / |z|
E = (0,1,0,0) : x-polarized linear
E = (0,0,1,0) : y-polarized linear
E = √[1/2] (0,1,1,0) : 45° from x-polarized linear
E = √[1/2] (0,1,i,0) : right-polarized circular
E = √[1/2] (0,1,-i,0) : left-polarized circular

General-polarized (elliptical)
E = (0,Cos[θ]Exp[iα_x],Sin[θ]Exp[iα_y]),0)
E* = (0,Cos[θ]Exp[-iα_x],Sin[θ]Exp[-iα_y]),0)

Note that the 4-Polarization has complex values in regular SR, and is the hint that QM is just complex values applied to SR.
=============================

SRQM 4-Vector : Four-Vector Compton Effect Diagram

The Compton Effect :
K·K = (ω_o/c)² = (1/cT_o)² = (m_oc/ћ)² = (1/λ_C)²
Now that there is a further relation between the 4-Momentum and the 4-WaveVector, we can now notice a few more constant relations based on the 4-WaveVector.
*Note* All values with strike-thru̇s are the reduced version of the regular values:
i.e. Reduced Compton Wavelength ( λ_C = λ_C/2π = ћ/m_oc ), Reduced Planck's Constant ( ћ = h/2π ), etc., and, of course, ( ω_o = 2πν_o )
The rest angular frequency ( ω_o ) is related to: the rest reduced period ( T_o ), the rest mass ( m_o ), and the Reduced Compton Wavelength ( λ_C ), which is *not* a rest wavelength.
The rest value of a massive particle would be when |k| = 0, which is the same as when the particle |λ| = Infinity.
The Compton Wavelength ( λ_C = h/m_oc ) is instead defined to be the wavelength of a photon with the equivalent energy of a massive particle of rest mass ( m_o ).
This can be seen in [K = (ω/c,k) = (1/cT,n̂/λ)]. The wavelength is set to the same value as c*period, which would make the 4-WaveVector a null or light-like 4-Vector.
The Compton Scattering Formula is Δλ = λ_C(1-cos[θ]) or Δλ = λ_C(1-cos[θ]) and is typically used to calculate the wavelength shift from the scattering of a photon off of an electron.
The effect was important for proving that light could not have a "wave-only" description, but that light as individual photons with momentum was necessary.
Compton Scattering Derivation
P·P = (m_oc)² generally → 0 for photons
P_phot1·P_phot2 = ћ²K₁·K₂ = (ћ²ω₁ω₂/c²)(1- n̂₁·n̂₂) = (ћ²ω₁ω₂/c²)(1-cos[ø])
P_phot·P_mass = ћK·P = (ћω/c)(1,n̂)·(E/c,p) = (ћω/c)(E/c- n̂·p) = (ћωE_o/c²) = (ћωm_o)
P_phot + P_mass = P'_phot + P'_mass:Conservation of 4-Momentum in Photon·Mass Interaction
===
P_phot + P_mass - P'_phot = P'_mass:rearrange
(P_phot + P_mass - P'_phot)² = (P'_mass)²:square to get scalars
(P_phot·P_phot + 2 P_phot·P_mass - 2 P_phot·P'_phot + P_mass·P_mass - 2 P_mass·P'_phot + P'_phot·P'_phot) = (P'_mass)²
(0 + 2 P_phot·P_mass - 2 P_phot·P'_phot + (m_oc)² - 2 P_mass·P'_phot + 0) = (m_oc)²
P_phot·P_mass - P_mass·P'_phot = P_phot·P'_phot
(ћωm_o)-(ћω'm_o) = (ћ²ωω'/c²)(1-cos[ø])
(ω-ω')/(ωω') = (ћ/m_oc²)(1-cos[ø])
(1/ω'-1/ω) = (ћ/m_oc²)(1-cos[ø])
(λ' - λ) = (ћ/m_oc)(1-cos[ø])
Δλ = λ_C(1-cos[ø]) : The Compton Effect
=============================

Quantum Superpostion :
Superposition is the simple mathematical consequence of the Klein-Gordon Equation being a linear PDE.
Any linear PDE (partial differential equation) will obey the principle of superposition.
This is a mathematical artifact of the KG Equation itself. It is not necessary as an additional axiom.
Klein-Gordon Equation: ∂·∂ = (-im_oc/ћ)² = -(m_oc/ћ)² = -(ω_o/c)²
Straight from standard calculus of PDĖs... find the particular solution and the homogeneous solutions...
K·K = (ω/c)² - k·k = (ω_o/c)²: The particular solution (with rest mass or rest frequency)
K_n·K_n = (ω_n/c)² - k_n·k_n = 0 : The homogeneous solution for a (virtual photon?) microstate (see Infraparticle, Soft Photon,)
Note that K_n·K_n = 0 is a null 4-Vector (photonic).
Let Ψ_p = a_pe^-i(K·X), then ∂·∂[Ψ_p] = (-i)²(K·K)Ψ_p = -(ω_o/c)²Ψ_p
which is the Klein-Gordon Equation particular solution...
Let Ψ_n = a_ne^-i(K_n·X), then ∂·∂[Ψ_n] = (-i)²(K_n·K_n)Ψ_n = (0)Ψ_n
which is the Klein-Gordon Equation homogeneous solution for a microstate (n).
We may now take Ψ = Ψ_p + Σ_nΨ_n
Note that the amplitude a_p and a_n's can be complex valued constants.
∂·∂[Ψ] = (-i)²[(K·K) + Σ_n(K_n·K_n)]Ψ = (-i)²[(K·K) + (0)]Ψ = -(ω_o/c)²Ψ
Thus there are any number of possible microstates (n) which solve the KG Equation.
Also note that since the homogeneous solutions are null, this could explain the apparent "extent" of a wavefunction beyond that of the particle.

The superposition prinicple allows the total phase to be a sum of individual phases.
Φ_Total = Φ_T = Σ_n(Φ_n) = Σ_n(- K_n·X) = -Σ_n(K_n·X)
K = - ∂[Φ] and Φ = - K·X : 4-WaveVector is negative 4-Gradient of SR Phase (Φ)
∂[Φ_T] = ∂[Σ_n(Φ_n)] = ∂[Σ_n(- K_n·X)] = ∂[-Σ_n(K_n·X)]
-∂[Φ_T] = -∂[Σ_n(Φ_n)] = -∂[Σ_n(- K_n·X)] = -∂[-Σ_n(K_n·X)]
-∂[Φ_T] = -∂[Σ_n(Φ_n)] = ∂[Σ_n(K_n·X)] = ∂[Σ_n(K_n·X)]
And that allows the Total 4-WaveVector to be a sum of individual 4-WaveVectors
K_T = -∂[Φ_T] = -∂[Σ_n(Φ_n)] = Σ_n(K_n)
(ћ)K_T = -(ћ)∂[Φ_T] = -(ћ)∂[Σ_n(Φ_n)] = (ћ)Σ_n(K_n) = Σ_n( (ћ)K_n)
(ћ)K_T = Σ_n( (ћ)K_n)
And that allows the Total 4-Momentum to be a sum of individual 4-Momenta
P_T = Σ_n(P_n)

∂[K] = [[0]]
∂[K_T] = ∂[Σ_n(K_n)] = Σn[[0]] = [[0]]
U·∂[K_T] = (d/dτ)[K_T] = U·[[0]] = Z = (0,0,0,0)
Take a guess where this is heading...
(ћ)U·∂[K_T] = (ћ)(d/dτ)[K_T] = (ћ)U·[[0]] = (ћ)Z = (ћ)(0,0,0,0) = (0,0,0,0)
U·∂[(ћ)K_T] = (d/dτ)[(ћ)K_T] = (0,0,0,0)
U·∂[P_T] = (d/dτ)[P_T] = Z = (0,0,0,0)
Conservation of Total 4-Momentum

The fact that Total 4-Momentum is conserved can be directly linked to two ideas:
(1) The fact that the KG equation, derived from SR, is a linear PDE, which has a linear superposition principle, giving sums of individual phases and waves.
(2) The fact that individual waves (4-WaveVectors) are not explicit functions of SpaceTime 4-Position.
In other words, the 4-WaveVectors are "carried" by the particles along their individual worldlines.
We know this is correct from single (photon/electron/atom/molecule) double-slit experiments.
The intensity can be reduced such that only a single photon is in the slit at a given time, yet the wave interference pattern builds up over repeated trials.
Also, the photon impacts are recorded on the screen as whole, individual particles.
Wave-particle duality is responsible for Conservation of Energy and Momentum.
=============================

Quantum Hilbert Space, Unitary Operators, Hermetian Generators, etc. :
Hilbert Space is the simple mathematical consequence of the Klein-Gordon Equation being a linear PDE.
As with superposition, Hilbert spaces occur as a consequence of the equation. They occur in contexts besides those of QM as well.
They are not necessary as an additional axiom.
From Wikipedia:
"Much of the mathematical machinery of quantum mechanics, such as state vectors, probability amplitudes, unitary operators, and Hermitian operators, emerge naturally from the classical Maxwell's equations in the description.
The quantum polarization state vector for the photon, for instance, is identical with the Jones vector, usually used to describe the polarization of a classical wave.
Unitary operators emerge from the classical requirement of the conservation of energy of a classical wave propagating through lossless media that alter the polarization state of the wave.
Hermitian operators then follow for infinitesimal transformations of a classical polarization state."
See:
Photon Polarization
Hilbert Space = Inner Product Space + Complete Metric Space
Koopman-von Neumann Classical Mechanics: using Hilbert Space descriptions for both classical and quantum
Being explicitly based on the Hilbert space language, the KvN classical mechanics adopts many techniques from quantum mechanics.
eg. Perturbation and diagram techniques as well as functional integral methods.
The KvN approach is very general, and it has been extended to dissipative systems, relativistic mechanics, and classical field theories.
The KvN approach is fruitful in studies on the quantum-classical correspondence as it reveals that the Hilbert space formulation is not exclusively quantum mechanical.
Even Dirac spinors are not exceptionally quantum as they are utilized in the relativistic generalization of the KvN mechanics.
Similarly to the more well-known phase space formulation of quantum mechanics,
the KvN approach can be understood as an attempt to bring classical and quantum mechanics into a common mathematical framework.
In fact, the time evolution of the Wigner function approaches, in the classical limit, the time evolution of the KvN wavefunction of a classical particle.
On Koopman-von Neumann Waves, On Koopman-von Neumann Waves II,
Hamilton-Jacobi Equation: motion of classical particles as waves
In physics, the Hamilton-Jacobi equation is an alternative formulation of classical mechanics, equivalent to other formulations such as:
Newton's laws of motion
Lagrangian mechanics
Hamiltonian mechanics.
The HJE is particularly useful in identifying conserved quantities for mechanical systems, which may be possible even when the mechanical problem itself cannot be solved completely.
The HJE is also the only formulation of mechanics in which the motion of a particle can be represented as a wave.
In this sense, the HJE fulfilled a long-held goal of theoretical physics of finding an analogy between the propagation of light and the motion of a particle.
The wave equation followed by mechanical systems is similar to, but not identical with, Schrödinger's equation.
For this reason, the HJE is considered the "closest approach" of classical mechanics to quantum mechanics
Bra-Ket Notation (aka Dirac Notation)
============================

The Schrödinger Quantum Wave Equation :
The Schrödinger QM Equation is simply the low-velocity limit of the KG Equation.
It is formally similar to a diffusion equation.

4-Momentum P = (E/c,p)
4-Gradient ∂ = (∂_t/c,-∇)
P = ħK = iħ∂ : The Schrödinger Relation which we derived from SR above
P = (E/c,p) = ħK = iħ∂ = iћ(∂_t/c,-∇)
or in component form, [E = iħ∂_t] and [p = -iħ∇]

∂·∂ = (∂_t/c)² -∇² = (im_oc/ћ)²: The Klein-Gordon Equation
P·P = (E/c)² - p² = (m_oc)²: Einstein Mass-Energy-Momentum Equivalence

E² = (m_oc²)² + c²p²: Einstein Relativistic Energy Relation
E = √[(m_oc²)² + c²p²]
E = (m_oc²)√[1 + (p²/(m_oc)²)]
E ~ (m_oc²) [1 + (p²/2(m_oc)²)] : Low velocity (|v| << c) Newtonian limiting-case using { √[1 + x] ~ (1 + x/2 + ...O[x²] ) }
E ~ [(m_oc²) + p²/2m_o] : Newtonian approximation gives Total Energy = Rest Energy + Kinetic Energy

(iħ∂_t) ~ [(m_oc²) + (-iħ∇)²/2m_o] : The Free Particle Schrödinger Equation
(iħ∂_t) ~ [(m_oc²) - (ħ∇)²/2m_o] : The Free Particle Schrödinger Equation

	Relativistic P = (E/c,p) = ħK = iħ∂ = iћ(∂_t/c,-∇)	Classical = limiting-case using { √[1 + x] ~ (1 + x/2 + ...O[x²] ) }
4-Momentum	Einstein Energy Relation P·P = (E/c)² - p² = (m_oc)²
solved for temporal component	E = √[(m_oc²)² + c²p²]	Newtonian Energy Relation E ~ [(m_oc²) + p²/2m_o]
4-Gradient	Free Particle Klein-Gordon RQM Equation ∂·∂ = (∂_t/c)² -∇² = (-im_oc/ћ)²iћ∂·iћ∂ = (iћ∂_t/c)² - (-iћ∇)² = (m_oc)²
solved for temporal component	(iћ∂_t) = √[(m_oc²)² + c²(-iћ∇)²] (iћ∂_t) = √[(m_oc²)² - c²(ћ∇)²]	Free Particle Schrödinger QM Equation (iħ∂_t) ~ [(m_oc²) + (-iħ∇)²/2m_o] (iħ∂_t) ~ [(m_oc²) - (ħ∇)²/2m_o]

=============================

The Schrödinger Quantum Wave Equation including the effects of a potential V :
The Schrödinger QM Equation is simply the low-velocity limit of the KG Equation.
It is formally similar to a diffusion equation, with the difference being the factor of i.
Here, I have used the Minimal Coupling relations, themselves based on 4-Vectors

4-Momentum P = (E/c,p)
4-Gradient ∂ = (∂_t/c,-∇)
4-VectorPotential A = (φ/c,a)
4-TotalMomentum P_T = (H/c,p_T) = (E_T/c + qφ/c,p + qa)
*Note*
The SR Phase Φ = -K·X = -(ω/c,k)·(ct,x) = -(ωt - k·x) = (-ωt + k·x)
The Scalar Potential φ is the temporal component of the 4-VectorPotential A = (φ/c,a)
These are not the same thing.

P = ħK = iħ∂ : The Schrödinger Relation which we derived from SR above
P_T = P + qA : The Total 4-Momentum = 4-Momentum of the Particle + 4-Momentum of the Potential
P = P_T - qA : Minimal Coupling Relation, just rearrangement of the 4-TotalMomentum

P = (E/c,p) = P_T - qA = (E_T/c - qφ/c,p_T - qa)
∂ = (∂_t/c,-∇) = ∂_T + (iq/ħ)A = (∂_tT/c + (iq/ħ)φ/c, -∇_T + (iq/ħ)a)

∂·∂ = (∂_t/c)² -∇² = (-im_oc/ћ)²
P·P = (E/c)² - p² = (m_oc)²: Einstein Mass-Energy-Momentum Equivalence

E² = (m_oc²)² + c²p²: Einstein Relativistic Energy Relation
E = √[(m_oc²)² + c²p²]
E = (m_oc²)√[1 + (p²/(m_oc)²)]
E ~ (m_oc²) [1 + (p²/2(m_oc)²)] : Low velocity (|v| << c) Newtonian limiting-case using { √[1 + x] ~ (1 + x/2 + ...O[x²] ) }
E ~ [(m_oc²) + p²/2m_o]

E² = (m_oc²)² + c²p²: Einstein Relativistic Energy Relation
E ~ [(m_oc²) + p²/2m_o]: Newtonian Energy Relation (the low velocity limiting-case)

(E_T -qφ)² = (m_oc²)² + c²(p_T -qa)²: Relativistic w Minimal Coupling
(E_T -qφ) ~ [(m_oc²) + (p_T -qa)²/2m_o] : Low velocity w Minimal Coupling

(iħ∂_tT -qφ)² = (m_oc²)² + c²(-iħ∇_T -qa)²: Relativistic w Minimal Coupling
(iħ∂_tT -qφ) ~ [(m_oc²) + (-iħ∇_T -qa)²/2m_o] : Low velocity w Minimal Coupling

(iħ∂_tT) ~ [qφ + (m_oc²) + (-iħ∇_T -qa)²/2m_o] : Low velocity w Minimal Coupling
(iħ∂_tT) ~ [V + (-iħ∇_T -qa)²/2m_o] : with [V = qφ + (m_oc²)]
(iħ∂_tT) ~ [V - (ħ∇_T)²/2m_o] : Typically the 3-vector-potential a~ 0 in many physical situations, esp. low velocity/low energy situations
(iħ∂_tT)| Ψ> ~ [V - (ħ∇_T)²/2m_o]| Ψ> : The Schrödinger Equation with potential ( = standard non-relativistic QM)

Note that most books don't mention that the 3-vector-potential (a) is actually required by Lorentz Invariance,
since its effects are typically small in the low-energy limit.
(iħ∂_t) ~ [(m_oc²) - (ħ∇)²/2m_o] : The Free Particle Schrödinger Equation

	Relativistic P = (E/c,p) = ħK = iħ∂ = iћ(∂_t/c,-∇) P_T = P + qA	Classical = limiting-case using { √[1 + x] ~ (1 + x/2 + ...O[x²] ) }
4-Momentum	Einstein Energy Relation P·P = (E/c)² - p² = (m_oc)² = (E_T/c - qφ/c)² - (p_T -qa)² = (m_oc)²
solved for temporal component	E = √[(m_oc²)² + c²p²] (E_T -qφ) = √[(m_oc²)² + c²(p_T -qa)²]	Newtonian Energy Relation E ~ [(m_oc²) + p²/2m_o] (E_T -qφ) ~ [(m_oc²) + (p_T -qa)²/2m_o]
4-Gradient	Free Particle Klein-Gordon RQM Equation ∂·∂ = (∂_t/c)² -∇² = (-im_oc/ћ)²iћ∂·iћ∂ = (iћ∂_t/c)² - (-iћ∇)² = (m_oc)² Klein-Gordon RQM Equation w/Potential (iħ∂_tT -qφ)² = (m_oc²)² + c²(-iħ∇_T -qa)²:
solved for temporal component	(iћ∂_t) = √[(m_oc²)² + c²(-iћ∇)²] (iћ∂_t) = √[(m_oc²)² - c²(ћ∇)²] (iħ∂_tT -qφ) = √[(m_oc²)² + c²(-iħ∇_T -qa)²] (iħ∂_tT) = qφ + √[(m_oc²)² + c²(-iħ∇_T -qa)²]	Free Particle Schrödinger QM Equation (iħ∂_t) ~ [(m_oc²) + (-iħ∇)²/2m_o] (iħ∂_t) ~ [(m_oc²) - (ħ∇)²/2m_o] Schrödinger QM Equation w/Potential (iħ∂_tT -qφ) ~ [(m_oc²) + (-iħ∇_T -qa)²/2m_o] (iħ∂_tT) ~ [qφ + (m_oc²) + (-iħ∇_T -qa)²/2m_o] (iħ∂_tT) ~ [V + (-iħ∇_T -qa)²/2m_o] : with [V = qφ + (m_oc²)] (iħ∂_tT) ~ [V - (ħ∇_T)²/2m_o]: with a = 0 the Standard way it is usually seen

=============================

More Relativistic Quantum Wave Equations :
∂·∂ + (m_oc/ћ)² = 0

(∂·∂ + (m_oc/ћ)² )Ψ = 0	Ψ is a scalar, Klein-Gordon eqn for massive spin-0 field, ex. the Higgs Boson
(∂·∂ + (m_oc/ћ)² )A = 0	A is a 4-Vector, Proca eqn for massive spin-1 field, Lorenz Gauge
(∂·∂)Ψ = 0	Ψ is a scalar, Free-wave eqn for massless (m_o = 0) spin-0 field
(∂·∂)A = 0	A is a 4-Vector, Maxwell eqn for massless (m_o = 0) spin-1 field, no current sources, Lorenz Gauge
(∂·∂)A = μ_oJ = ρ_oμ_oU = qn_oμ_oU = qμ_oN	A is a 4-Vector, Maxwell eqn for massless (m_o = 0) spin-1 field, current source J, Lorenz Gauge Classical EM, does not include effects of particle spin in the current source J
(∂·∂)A = μ_oJ = μ_o(qΨ ̅ γΨ) (∂·∂)A^μ = μ_oJ = μ_o(qΨ ̅ γ^μΨ) where Ψ ̅ γ^μΨ has units of flux (#/m²·s)	QED, A is a 4-Vector, Maxwell eqn for massless (m_o = 0) spin-1 field, current source J, Lorenz Gauge Quantum EM, does include effects of particle spin in the current source J = Ψ ̅ γ^μΨ
Just a note: The classical Maxwell EM equations do not have Spin included (∂·∂)A_EM = μ_oJ = μ_oρ_oU = μ_oqn_oU = μ_oqN = μ_o(q/V_o)U = μ_oq(c/V_o)T Once spin is included, the equations for QED emerge: (∂·∂)A_EM = μ_oqψ Γψ not sure if the μ_o factor is included or not

=============================

Conservation of Probability, Conservation of Probability Current, Conservation of Charge Current :
see also Probability Current, 4-CurrentDensity,
Consider the following purely mathematical argument (based on Green's Vector Identity):
∂·( f ∂[g] - ∂[f] g ) = f ∂·∂[g] - ∂·∂[f] g, with f and g as SR Lorentz Scalar functions

∂·( f ∂[g] - ∂[f] g )
= ∂·( f ∂[g] ) - ∂·(∂[f] g )
= (f ∂·∂[g] + ∂[f]·∂[g]) - (∂[f]·∂[g] + ∂·∂[f] g)
= f ∂·∂[g] - ∂·∂[f] g

So, f ∂·∂[g] - ∂·∂[f] g = ∂·( f ∂[g] - ∂[f] g )
I can also multiply this by a Lorentz Invariant Scalar Constant s
s (f ∂·∂[g] - ∂·∂[f] g) = s ∂·( f ∂[g] - ∂[f] g ) = ∂·s( f ∂[g] - ∂[f] g )
Ok, so we have the math that we need...

Now, on to the physics...
∂·∂ = (-im_oc/ћ)² = -(m_oc/ћ)²: The Klein-Gordon Eqn
∂·∂ + (m_oc/ћ)² = 0

Let it act on Lorentz Invariant function g
∂·∂[g] + (m_oc/ћ)²[g] = 0 [g]
Then pre-multiply by f
[f]∂·∂[g] + [f] (m_oc/ћ)²[g] = [f] 0 [g]
Resulting in
[f] ∂·∂[g] + (m_oc/ћ)²[f][g] = 0

Now, do similarly with Lorentz Invariant function f
∂·∂[f] + (m_oc/ћ)²[f] = 0 [f]
Then post-multiply by g
∂·∂[f][g] + (m_oc/ћ)²[f][g] = 0 [f][g]
Resulting in
∂·∂[f][g] + (m_oc/ћ)²[f][g] = 0

Now, subtract the two equations
{[f] ∂·∂[g] + (m_oc/ћ)²[f][g] = 0} - { ∂·∂[f][g] + (m_oc/ћ)²[f][g] = 0}
Resulting in
[f] ∂·∂[g] + (m_oc/ћ)²[f][g] - ∂·∂[f][g]- (m_oc/ћ)²[f][g] = 0
[f] ∂·∂[g] - ∂·∂[f][g] = 0

And as we noted from the mathematical identity at the start...
[f] ∂·∂[g] - ∂·∂[f][g] = ∂·( f ∂[g] - ∂[f] g ) = 0
s ([f] ∂·∂[g] - ∂·∂[f][g]) = s ∂·( f ∂[g] - ∂[f] g ) = s 0 = 0

Therefore,
s ∂·( f ∂[g] - ∂[f] g ) = 0
∂·s( f ∂[g] - ∂[f] g ) = 0

There is a conserved current 4-Vector, J_prob = s ( f ∂[g] - ∂[f] g ), for which ∂·J_prob = 0, and which also solves the Klein-Gordon equation.

Let's choose as before (∂ = -i K) with a plane wave function f = ae^-i(K·X), and choose g = f* = ae^i(K·X) as its complex conjugate.
At this point, I am going to choose s = (iћ/2m_o), which is Lorentz Scalar Invariant, in order to make the probability have dimensionless units and be normalized to unity in the rest case.

Then J_prob = s ( f ∂[g] - ∂[f] g ) = s{f (-i)Kg} - s{i Kf g} = s (-2i)Kfg
J_prob = -2is Kfg
J_prob = (ρ_probc,j_prob) = -2is Kfg = -2is (ω/c,k) fg

Now, take the temporal component
ρ_probc = -2is (ω/c) fg
ρ_prob = -2is (ω/c²) fg
ρ_prob = -2i (iћ/2m_o)(γω_o/c²) fg
ρ_prob = (-i²)(2/2)(ћω_o/m_oc²)(γ) fg
ρ_prob = (γ) fg

Now, to put it in a more obvious form... f = ψ*, g = ψ
I have put off using psi until now to point out that (f and g) could have been any kind of SR Lorentz Invariant functions for this derivation.
ρ_prob = (γ)(ψ*ψ) = (γ)(ρ_o)

(ρ_{o_prob}) = (ψ*ψ) = fg
The probability density ρ_prob = γρ_{o_prob} is only equal to (ψ*ψ) in the Newtonian low-energy limiting-case with γ → 1
Thus, the Born Probability Amplitude Interpretation of (ψ*ψ) only applies in the Newtonian low-energy limiting-case

J_prob = s ( f ∂[g] - ∂[f] g ) = (iћ/2m_o)( ψ* ∂[ψ] - ∂[ψ*] ψ )
J_prob = (iћ/2m_o)( ψ* ∂[ψ] - ∂[ψ*] ψ )

Also, we know that J = ρ_oUand K = P/ћ = (m_o/ћ)U
J_prob = (ρ_{o_prob})(ћ/m_o)K
J_prob = (fg)(-2is)K
So, everything matches correctly

J_prob = ρ_{o_prob}U = (ψ*ψ)U
J_charge = qJ_prob

J_charge = qρ_{o_prob}U = q(ψ*ψ)U
If we do the calculation including an EM potential, then the 4-ProbabilityCurrentDensity gains an extra component

From before: J = -2is Kfg

Minimal Coupling is just observation that the 4-TotalMomentum is the sum of the particle 4-Momentum and the field 4-PotentialMomentum
We have conservation of the Total 4-Momentum P_T
P_T = P + qA
P = P_T - qA
K = K_T - (q/ћ)A

J_prob = -2is(K)fg
J_prob = -2is(K_T - (q/ћ)A)fg
J_prob = -2is(K_T)fg + 2is(q/ћ)A)fg

J_prob = (iћ/2m_o)( ψ* ∂[ψ] - ∂[ψ*] ψ ) + 2is(q/ћ)Afg
J_prob = (iћ/2m_o)( ψ* ∂[ψ] - ∂[ψ*] ψ ) + 2i(iћ/2m_o)(q/ћ)Afg
J_prob = (iћ/2m_o)( ψ* ∂[ψ] - ∂[ψ*] ψ ) - (q/m_o)Afg

J_prob = (iћ/2m_o)( ψ* ∂[ψ] - ∂[ψ*] ψ ) - (q/m_o)A(ψ*ψ)
J_prob = (1/2m_o)( ψ* P[ψ] - P[ψ*] ψ ) - (q/m_o)A(ψ*ψ), using the operator version of P
J_prob = (1/2m_o)[( ψ* P[ψ] - P[ψ*] ψ ) - (2q)A(ψ*ψ)], using the operator version of P

J_charge = qJ_prob
J_charge = q[(iћ/2m_o)( ψ* ∂[ψ] - ∂[ψ*] ψ ) - (q/m_o)A(ψ*ψ)]
J_charge = (iћq/2m_o)( ψ* ∂[ψ] - ∂[ψ*] ψ ) - (q²/m_o)A(ψ*ψ)
4-ProbabilityCurrentDensity J_prob = (iћ/2m_o)( ψ* ∂[ψ] - ∂[ψ*] ψ ) - (q/m_o)A(ψ*ψ)
4-ChargeCurrentDensity J_charge = qJ_prob

If instead one starts with a Dirac eqn instead of the Klein-Gordon, one gets:
(Γ·P) - (m_oc) = 0
(Γ^μP_μ) - (m_oc) = 0
iћ(Γ^μ∂_μ) - (m_oc) = 0
(Γ^μ∂_μ) - (m_oc/iћ) = 0

Let it act on Lorentz Invariant function g
(Γ^μ∂_μ) - (m_oc/iћ)[g] = 0 [g]
Then pre-multiply by f
[f](Γ^μ∂_μ)[g] - [f] (m_oc/iћ)[g] = [f] 0 [g]
Resulting in
[f](Γ^μ∂_μ)[g] - (m_oc/iћ)[f][g] = 0

Now, do similarly with Lorentz Invariant function f
(Γ^μ∂_μ)[f] - (m_oc/iћ)[f] = 0 [f]
Then post-multiply by g
(Γ^μ∂_μ)[f][g] - (m_oc/iћ)[f][g] = 0 [f][g]
Resulting in
(Γ^μ∂_μ)[f][g] - (m_oc/iћ)[f][g] = 0

Now, subtract the two equations
{[f] (Γ^μ∂_μ)[g] - (m_oc/iћ)[f][g] = 0} - { (Γ^μ∂_μ)[f][g] - (m_oc/iћ)[f][g] = 0}
Resulting in
[f] (Γ^μ∂_μ)[g] + (m_oc/iћ)[f][g] - (Γ^μ∂_μ)[f][g]+ (m_oc/iћ)[f][g] = 0
[f] (Γ^μ∂_μ)[g] - (Γ^μ∂_μ)[f][g] = 0

If we let [f] = ψ̅ = ψ*γ⁴ and [g] = ψ

ψ̅ (Γ^μ∂_μ)[ψ] - (Γ^μ∂_μ)[ψ̅ ]ψ = 0
ψ̅ (Γ^μ∂_μ)[ψ] + (∂_μ)[ψ̅ ]Γ^μψ = 0 ******** This is the Dirac Adjoint Magic *** Need to double-check this ***
(∂_μ) {ψ̅ (Γ^μ) ψ + ψ̅ Γ^μ ψ} = 0
(∂_μ) {2ψ̅ (Γ^μ) ψ} = 0
(∂_μ) {ψ̅ (Γ^μ) ψ} = 0
(∂_μ) {J_prob^μ} = 0

4-ProbabilityCurrentDensity J_prob = ψ̅ Γ^μ ψ
4-ChargeCurrentDensity J_charge = qJ_prob

Note: Check the dimensional units and what the 4-Vector is describing.
4-ProbabilityCurrentDensity J_prob describes the "probability density", a numerical value, of a particle being in a particular place.
4-NumberFlux N_f describes the "number density", a numerical value, of a particle, or continuous fluid, being in a particular place.
These are really the same concept, with the 4-NumberFlux definitely derived exclusively from SR fluid tensor mechanics, and the 4-ProbabilityCurrentDensity originally thought to have been derived from RQM.
But, we see that they are really both the same SR concept.
4-ProbabilityCurrentDensity J_prob = (iћ/2m_o)( ψ* ∂[ψ] - ∂[ψ*] ψ ) - (q/m_o)A(ψ*ψ)
4-NumberFlux N = N^μ = N_f = n(c,u) = (cn,nu) = (cn,n) = Σ_a[∫dτ δ⁽⁴⁾[X - X_a(τ)]dX_a/dτ]
=============================

Harmonic Oscillation of Position and Momentum Operators :
I'm not sure of the validity of this, but it's interesting...
U·∂ = γ(∂/∂t +U·∇) = γd/dt = d/dτ
d/dτ = U·∂
d/dτ = U·(-i K)
d/dτ = U·(-i/ћP)
d/dτ = U·(-im_o/ћU)
d/dτ = (-im_o/ћ)U·U
d/dτ = (-im_oc²/ћ)
d/dτ = (-iω_om_oc²/ћω_o)
d/dτ = (-iω_o)
d²/dτ² = -(ω_o)²
Now, apply this to the 4-Position...
d² X/dτ² = -(ω_o)² X
This is the differential equation of a relativistic harmonic oscillator.
Quantum events oscillate at their rest-frequency ω_o.
Likewise for the 4-Momentum:
d² P/dτ² = -(ω_o)² P
=============================

Creation/Annihilation Operators and Second Quantization :
One can then apply the {Creation/Annihilation} Operator Formalism:
see also: Fock Space, Second Quantization,
This is purely a mathematical definition, it is not a QM axiom.
One simply defines an SR function of X and ∂
A^t = √[1/2](X/l_o + l_o∂)
A = √[1/2](X/l_o - l_o∂)
with ( ћ/m_oω_o = ћω_oc²/m_oω_o²c² = c²/ω_o² = l_o² = {length²})
Note that this makes the A and A^t 4-Vectors dimensionless
Also, I need to double-check minus sign conventions here..., I might have them backwards

solving for X and ∂gives:
X = l_o/(√2) (A^t + A) = √[ћ/(2m_oω_o)] (A^t + A)
∂ = 1/(l_o√2) (A^t - A) = √[m_oω_o/(2ћ)] (A^t - A)
P = iћ∂ = i√[m_oω_oћ/2] (A^t - A)

from before:
[∂,X] = ∂[X] = (∂_t/c,-∇)[(ct,r)] = (∂_t/c,-∂_x,-∂_y,-∂_z)[(ct,x,y,z)] = Diag[+1,-1,-1,-1] = η^uv = Minkowski Metric
one can show that:
A^tA = (1/2)(X²/l_o² - η^uv - l_o² ∂²) = n̂ (a Number Operator)
AA^t = (1/2)(X²/l_o² + η^uv - l_o² ∂²)

[A,A^t] = (1/2)(2η^uv) = η^uv
[n̂,A^t] = [A^t A,A^t] = (A^t A)(A^t)-(A^t)(A^t A) = (A^t)(AA^t) - (A^t)(A^t A) = (A^t)(AA^t - A^t A) = (A^t)[A,A^t] = (A^t)η^uv
[n̂,A^t] = (A^t) η^uv
[n̂,A] = -(A) η^uv

more to come...

Now for fermions, we use the anti-commutation relations from the Dirac Eqn. instead:
(γ⁰p⁰ - γ·p)Ψ = (Γ·P)Ψ = (m_oc)Ψ
(Γ·P) = (Γ^μP_μ) = iћ(Γ^μ∂_μ) = (m_oc)

{Γ^μ,Γ^ν} = 2η^μνI₄

The Spin Lie Algebra {in the (3,1) convention, which fits the complexified CL_3,1(ℝ)_ℂ} is given by:
[Γ^μ,Γ^ν] = 4i σ^μν
[σ^μν, σ^ρτ] = i( η^μρσ^ντ - η^νρσ^μτ + η^ντσ^μρ - η^μτσ^νρ)
See Clifford Algebra,
Importantly, the Clifford Algebra of SpaceTime used in physics has more structure than CL₄(ℂ).
It has in addition a set of preferred transformations - the Lorentz Transformations.
See derivation of Dirac Equation from 4-Vector formalism further below...

Next to show Gordon Decomposition of Spin stuff...
=============================

The Correspondence Principle and Non-Relativistic fallacies :
There are two Correspondence Principles that have been used historically:
(1) The Relativistic → Classical Correspondence
(2) The Quantum → Classical Correspondence

The Relativistic → Classical Correspondence is very easy to understand.
It is simply the idea that Classical = lim_{(|v| << c)}[Relativistic]
P·P = (E/c)² - p² = (m_oc)²: Einstein Mass-Energy-Momentum Equivalence
E² = (m_oc²)² + c²p²: Einstein Relativistic Energy Relation
E = √[(m_oc²)² + c²p²]
E = (m_oc²)√[1 + (p²/(m_oc)²)]
E ~ (m_oc²) [1 + (p²/2(m_oc)²) + ...] : Low velocity (|v| << c) Newtonian limiting-case using { √[1 + x] ~ (1 + x/2 + ...O[x²] ), itself a specific case of (1+x)ⁿ ~ 1 + nx + ...O[x²] }
E ~ [(m_oc²) + p²/2m_o + ...] : Newtonian approximation gives Total Energy = Rest Energy + Kinetic Energy

The Quantum → Classical Correspondence Principle says that QM should give the same results as classical physics in the realm of large quantum systems,
i.e. where macroscopic behavior overwhelms quantum effects.
Another way to state this is where the change of a single quantum has a neglible effect on the overall state.

There is a way to derive this limit, by using Hamilton-Jacobi Theory:
(iħ∂_t)Ψ = [V - (ħ∇)²/2m_o]Ψ : The Schrödinger NRQM Equation for a point particle in a potential (non-relativistic QM)

Examine solutions of form Ψ = Ψ_oe^i(S/ħ), where S is the QM Action
∂_t[Ψ] = (i/ħ)Ψ∂_t[S]
∇[Ψ] = (i/ħ)Ψ∇[S]
∇²[Ψ] = (i/ħ)Ψ∇²[S] - (Ψ/ħ²)(∇[S])²

(iħ∂_t)Ψ = [V - (ħ∇)²/2m_o]Ψ
(iħ)∂_tΨ = VΨ - (ħ²/2m_o)∇²Ψ
(iħ)(i/ħ)Ψ∂_t[S] = VΨ - (ħ²/2m_o)[(i/ħ)Ψ∇²[S]-(Ψ/ħ²)(∇[S])²]
(i)(i)Ψ∂_t[S] = VΨ - (iħ/2m_o)Ψ∇²[S] - (Ψ/2m_o)(∇[S])²
-Ψ∂_t[S] = VΨ - (iħ/2m_o)Ψ∇²[S] - (Ψ/2m_o)(∇[S])2
∂t[S] = -V + (iħ/2m_o)∇²[S] - (1/2m_o)(∇[S])²

∂t[S] + V + (1/2m_o)(∇[S])² = (iħ/2m_o)∇²[S] : Quantum Single Particle Hamilton-Jacobi
∂t[S] + V + (1/2m_o)(∇[S])² = 0 : Classical Single Particle Hamilton-Jacobi

Note the p = ∇[S]
Thus, according to Goldstein, Classical Mechanics, 2nd.Ed., the classical limiting-case is:
ħ∇²[S] << (∇[S])²
ħ∇∙p << (p∙p)
(pλ)∇∙p << (p∙p)
(λ/p)∇∙p << 1

However, it can be shown that it does not depend on the size of ħ.
Note that { S = ħΦ , p = ħk , k = ∇[Φ] }
ħ∇²[S] << (∇[S])²
∇²[Φ] << (∇[Φ])²
∇∙k << (k∙k)
It does not depend on the size of ħ.
It is purely due to wave phase and/or wavevector behavior, where the magnitude of the source/sink of k << total magnitude of k.

====
However, we can do better... Start instead with the relativistic KG equation:
∂·∂ = (-im_oc/ћ)² = -(m_oc/ћ)² = -(ω_o/c)²
P_T = -∂[S] and P = P_T - qA
P·P = (m_oc)²
( -∂[S] - qA)·( -∂[S] - qA) = (m_oc)²
(∂[S] + qA)·(∂[S] + qA) = (m_oc)²

Examine solutions of form Ψ = Ψ_oe^i(S/ħ), where S is the RQM Action
∂[Ψ] = (i/ħ)Ψ ∂[S]
∂·∂[Ψ] = (i/ħ)Ψ ∂·∂[S] - (Ψ/ħ²)(∂[S])²
but ∂·∂ = -(m_oc/ћ)²

-(m_oc/ћ)² = (i/ħ)∂·∂[S] - (1/ħ²)(∂[S])²
(1/ħ²)(∂[S])² - (m_oc/ћ)² = (i/ħ)∂·∂[S]
(∂[S])² - (m_oc)² = (iħ)∂·∂[S]: The RQM version
P_T·P_T - (m_oc)² = (-iħ)∂·P_T: The RQM version

(∂[S] + qA)·(∂[S] + qA) = (m_oc)²
(- P_T + qA)·(- P_T + qA) = (m_oc)²
P_T·P_T -qP_T·A -qA·P_T + q²A·A - (m_oc)² = 0
Examine the case when there is no 4-VectorPotential...
P_T·P_T - (m_oc)² = 0: The Classical Relativistic version
P_T·P_T - (m_oc)² = (-iħ)∂·P_T: The RQM version

and back to
P_T·P_T >> |(-iħ)∂·P_T|
but again, doesn't depend on size of ħ, because:
K_T·K_T >> |(-i)∂·K_T|: The magnitude squared of the 4-TotalWaveVector >> Magnitude of the 4-Divergence of the 4-TotalWaveVector

more interesting though is:
P_T·P_T -qP_T·A -qA·P_T + q²A·A - (m_oc)² = 0
P_T·P_T - (m_oc)² = +qP_T·A +qA·P_T - q²A·A
P_T·P_T - (m_oc)² = (-iħ)∂·P_T: The RQM version
(-iħ)∂·P_T = +qP_T·A +qA·P_T - q²A·A
(iħ)∂·P_T = -qP_T·A -qA·P_T + q²A·A
This probably means that quantum effects only occur when the particle is interacting with some kind of potential

** Note **
In this treatise,
GR is our starting point.
SR = lim_{(curvature~0)}[GR]
RQM = SR + the few empirical observations
U = dR/dτ
P = m_oU
K = (1/ћ)P = (ω_o/c²)U
∂ = -iK
QM = lim_{(|v| << c)}[RQM]
CM = lim_{(KT·KT >> |(-i)∂·KT|)}[QM]
Note that CM is removed from SR by two separate limiting-cases.
In the old paradigm, these were indepedent limiting-cases.
In the new paradigm, these are sequential limiting-cases.
QM is itself a limiting-case of RQM.

This has led to a number of fallacies that need to be addressed.
Starting with a easy case:
If one is starting in CM, one gets the principle that velocity is additive (v₁₂ = v₁ + v₂).
This is true only in the cases when |v| << c.
The fallacy comes when trying to use the principle outside of its domain of validity, and leads to the idea of unlimited speed in CM.
The correct law is the Relativistic Composition of Velocities
u_rel =
= [u₁ +u₂]/(1 + β₁·β₂)
= [u₁ +u₂]/(1 +u₁·u₂/c²)
which imposes the Universal Speed Limit of c.

Another not well known one is the Born Probability Interpretation.
The "classical" QM definition is the that (ψ*ψ) represents a probability density.
And in most cases that definition works well.
However, the relativistically correct definition is ρ_prob = (γ)(ψ*ψ) = (γ)(ρ_o)
The probability density ρ_prob = γρ_{o_prob} is only equal to (ψ*ψ) in the Newtonian low-energy limiting-case with γ → 1.
Thus, the Born Probability Interpretation of (ψ*ψ) only applies in the Newtonian low-energy limiting-case.
The probability density is actually just the temporal component of the a 4-Vector:
4-ProbabilityCurrentDensity J_prob = (iћ/2m_o)( ψ*∂[ψ] - ∂[ψ*]ψ ) - (q/m_o)A(ψ*ψ)
J·U = (ρc,j)·γ(c,u) = γ(ρc² - j·u) = ρ_oc²
∂·J = (∂_t/c,-∇)·(ρc,j) = (∂_tρ + ∇·j) = 0 {if conservative}
The relativistic/covariant versions are always true for all observers.
In other words, the local movement of probability is always conserved.
However, different observers will see different amounts in the components, per standard 4-Vector rules.

Now then, let's examine the "non-local" quantum potential of De Broglie-Bohm Theory.
The fallacy is once again assuming that it has an unlimited range of validity.
The problem is that is based on the Schrödinger equation, which is QM, which means that it is the Newtonian approximation (|v| << c) of RQM.
It has the exact same problem as the unlimited velocity of CM.
The "non-local" character is caused by trying to use QM (with unlimited |v|) outside of its range of validity (|v| << c).

Re-visiting the 4-Momentum :
4-Momentum P = (E/c,p) = (mc,p)
P = m_oU = (E_o/c²)U
gives the Energy-Momentum content of an SR particle at a particular event: SI Units [kg·m/s].
E is the energy ( = temporal momentum) of the event and p is the spatial momentum.
The 4-Momentum is sort of a staging point about which a lot of physics takes place.
P = m_oU = (E_o/c²)U : Related to motion
P = P_T - qA : Related to the 4-TotalMomentum of a system which can include the effects of a 4-VectorPotential
P = - ∂[S] - qA : Related to the 4-Gradient of the action of a system
P = ћK : Related to waves
P = iħ∂ : Related to quantum operators, which are themselves just the SR 4-Gradient operator
=============================

Re-visiting the 4-Gradient :
The 4-Gradient ∂ = ∂_X = (∂_t/c,-∇) = (∂_t/c,- del) → (∂_t/c, -∂_x, -∂_y,-∂_z) = (∂/c∂t,-∂/∂x,-∂/∂y,-∂/∂z) is an SR functional that gives the structure of Minkowski SpaceTime.
∂_t is the partial wrt. time and ∇ is the gradient, the partial vector wrt. spatial dimensions (eg. {x,y,z} or {r,θ,z} or {r,θ,φ}, etc.).
The Lorentz Scalar Product ∂·∂ = (∂_t/c,-∇)·(∂_t/c,-∇) = (∂_t/c)² - ∇·∇ = (∂_τ/c)²
gives the d'Alembertian equation (a wave equation).
When the spatial part ∇ is 0, this gives a Lorentz invariant rest partial∂_to = ∂_τ., which would presumably be the partial as measured along a worldline.
The d'Alembert operator (∂·∂) is the Laplace operator of Minkowski Space. Despite being a functional, the d'Alembertian is still a Lorentz Scalar Invariant.
The Green's function G[X - X'] for the d'Alembertian is defined as (∂·∂)G[X - X'] = δ⁴[X - X'], with (δ⁴) as the 4-D Dirac Delta.
Gauss' Theorem in SR is { ∫_Ωd⁴X (∂·V) = ∮_∂ΩdS (V·N) }
where Ω is a 4D simply-connected region of Minkowski SpaceTime, ∂Ω = S is its 3D boundary with its own 3D Volume element dS and outward pointing normal N^μ.
The 4-Gradient is used in many ways in SR and QM:
===
(*) As a 4-Divergence and source of Conservation Laws:
∂·X = (∂_t/c,-∇)·(ct,x) = (∂_t[ct]/c) - (-∇·x) = (∂_t[t]) + (∇·x) = (∂_t[t]) + (∂_x[x] + ∂_y[y] + ∂_z[z]) = (1) + (3) = 4: Dimension of SpaceTime is 4
∂·J = (∂_t/c,-∇)·(cρ,j) = (∂_t[cρ]/c) - (-∇·j) = (∂_t[ρ]) + (∇·j) = 0: Continuity eqn/Conservation of 4-CurrentDensity
∂·N = (∂_t/c,-∇)·(cn,n) = (∂_t[cn]/c) - (-∇·n) = (∂_t[n]) + (∇·n) = 0: Continuity/Conservation of 4-NumberFluxDensity (typically something like a baryon number density)
∂·A_EM = (∂_t/c,-∇)·(φ/c,a) = (∂_t[φ]/c²) - (-∇·a) = (∂_t[φ]/c²) + (∇·a) = 0: Lorenz Gauge Condition/Continuity eqn/Conservation of 4-EM-VectorPotential
∂·h_TT^μν = ∂_μh_TT^μν = 0^ν: Lorenz Gauge Condition/Continuity eqn/Conservation of Freely Propagating Gravitational Wave (far field approx.)
∂_νT^μν = Z^μ = 0^μ: Continuity/Conservation of the Stress-Energy Tensor = 4 Conservation Laws = 1 Energy Conservation + 3 Linear Momenta Conservation
∂_ν( X^αT^μν - X^μT^αν) = 0^αμ: Conservation of Angular Momentum
When these last two are combined, and the Stress-Energy is for a perfect fluid, one can derive the relativistic Euler equations.
When GR effects are required, one uses the "comma to semi-colon rule"
∇_βV^α = ∂_βV^α + V^μΓ^α_μβ
V^α_;β = V^α_,β + V^μΓ^αμβ
===
(*) As a Jacobian matrix for the SR Metric:
∂[X] = ∂^μX^ν = (∂_t/c,-∇)(ct,x) = Diag[+1,-1,-1,-1] = Diag[+1,-1] = η^μν
∂^μX^ν = η^μσ∂_σX^ν = η^μσ(∂/∂X^σ)X^ν = η^μσ(∂X^ν/∂X^σ) = η^μσ(δ_σ^ν) = η^μν
===
(*) As part of the total proper time derivative
U·∂ = γ(c,u)·(∂_t/c,-∇) = γ(∂_t +U·∇) = γ(d/dt) = d/dτ
d/dτ = (dX/dX)(d/dτ) = (dX/dτ)(d/dX) = U^μ∂_μ = U·∂
d/dτ [X] = (U·∂)X = U
d/dτ [U] = (U·∂)U = A
===
(*) As a way to define the Faraday EM Tensor and derive the Maxwell Eqns
F^μν = (∂^μA_EM^ν - ∂^νA_EM^μ) =

[ 0 ,-e^x/c,-e^y/c,-e^z/c]
[e^x/c, 0 , -b^z , b^y ]
[e^y/c, b^z , 0, -b^x ]
[e^z/c, -b^y, b^x , 0] =

[ 0, -eⁱ/c ]
[+ eⁱ/c,-ε_ijkb^k]

Maxwell Eqns:
∂_αF^αν = μ_oJ^ν
∂^α F^μν + ∂^ν F^αμ + ∂^μ F^να = 0
===
(*) As a way to define the 4-WaveVector
K = -∂[Φ]
K·X = -Φ
∂[K·X] = ∂[-Φ] = ∂^w[η_uvK^uX^v] = ∂^w[K_vX^v] = K_v∂^w[X^v] + X^v∂^w[K_v] = K_vη^wv + [0] = K^w = K·∂[X] + ∂[K]·X = K
ψ_n(X) = A_ne^-i(K_n·X), the explicit form of an SR plane wave
ψ(X) = Σ_n[ ψ_n(X) ], the complete wave is a superposition of multiple plane waves
∂[ ψ(X) ] = ∂[ Ae^-i(K·X) ] = -iK [ Ae^-i(K·X) ] = -iK[ ψ(X) ]
or, finally, ∂ = -iK as the condition for a complex-valued plane wave.
where it is assumed that the 4-WaveVector is not an explicit function of 4-Position, i.e. ∂[K] = [0]
===
(*) As the d'Alembertian Operator
The Lorentz Scalar Product ∂·∂ = (∂_t/c,-∇)·(∂_t/c,-∇) = (∂_t/c)² - ∇·∇ = (∂_τ/c)²
gives the d'Alembertian equation (a wave equation) for all types of fields/wavefunctions.
All of the following are in Lorenz Guage (∂·A) = 0

{with mass}
(∂·∂)Ψ = -(m_oc/ћ)²Ψ : The Klein-Gordon Spin-0 Equation
(∂·∂)A^ν = -(m_oc/ћ)²A^ν: The Proca Spin-1 Equation
{massless}
(∂·∂)Ψ = 0: The Free Massless Scalar Spin-0 Equation
(∂·∂)A^ν = 0^ν: The Free Classical Maxwell EM Equation {no source, no spin}
(∂·∂)A^ν = μ_oJ^ν: The Classical Maxwell EM Equation {with 4-Current J source, no spin}
(∂·∂)A^ν = q(ψ̅ γ^ν ψ): The QED Maxwell EM Spin-1 Equation {with QED source, including spin}

(∂·∂)h_TT^μν = 0^μν: The far-field freely-propagating Gravitational Wave Equation
further conditions on h_TT^μν are (the _TT stands for Transverse-Traceless):
U·h_TT^μν = U_μh_TT^μν = 0^ν: Purely spatial {because orthognal to 4-Velocity, with is purely temporal}
∂·h_TT^μν = ∂_μh_TT^μν = 0^ν: Transverse
Tr[h_TT^μν] = η_μνh_TT^μν = 0: Traceless

(∂·∂)G[X-X'] = δ⁽⁴⁾[X-X'] : The 4D version of Green's function
where δ⁽⁴⁾[X] = (1/(2π)⁴) ∫d⁴K e^-i(K·X)

===
(*) As a component of the 4D Gauss' Theorem
Gauss' Theorem in SR is { ∫_Ωd⁴X ∂_μV^μ = ∮_∂ΩdS V^μN_μ}
Gauss' Theorem in SR is { ∫_Ωd⁴X (∂·V) = ∮_∂ΩdS (V·N) }
where:
Ω is a 4D simply-connected region of Minkowski SpaceTime
∂Ω = S is its 3D boundary with its own 3D Volume element dS and outward pointing normal N.
d⁴X = (c dt)(d³x) = (c dt)(dx dy dz) is the 4D differential volume element

===
(*) As a component of the SR Hamilton-Jacobi equation in relativistic analytic mechanics
P_T = (E_T/c,p_T) = (H/c,p_T) = P + qA = - ∂[S] = (-∂_t[S]/c,∇[S]), where (H) is the Hamiltonian and (S) is the action.
(P·P) = (m_oc)²
(P_T - qA)·(P_T - qA) = (m_oc)²
(- ∂[S] - qA)·(- ∂[S] - qA) = (m_oc)²
(∂[S] + qA)·(∂[S] + qA) = (m_oc)²
===
Up to this point, all relations have used the 4-Gradient in a purely SR way.
Now note that there is no huge difference when bringing the 4-Gradient into play for QM.
Also note, the 4-Gradient is in SR already an operator - This doesn't need to be a quantum axiom.
===
(*) As a component of the Schrödinger Relations in QM
P = (E/c,p) = iћ∂ = iћ(∂_t/c,-∇).
The temporal eqn. is { E = iћ∂_t}, the Schrödinger QM Energy
The spatial eqn. is { p = -iћ∇}, the Schrödinger QM 3-momentum Relations.
This is easy decomposed into two separate steps
P = (E/c,p) = ћK = ћ(ω/c,k). The combo of the Planck-Einstein { E = ћω } and de Broglie { p = ћk} matter wave equations.
K = (ω/c,k) = i∂ = i (∂_t/c,-∇). The gradient version {ω = i∂_t,k = -i∇)} of the complex plane wave equation.
===
(*) As a component of the quantum canonical commutation relation
[∂,X] = ∂[X] = η^μν

[∂,X] = η^μν
[K,X] = iη^μν
[P,X] = iћη^μν

[X^μ,P^ν] = - iћη^μνand, looking at just the spatial part...

[x_j,p_k] = iћδ_jk

also
[X⁰,P⁰] = [ct,E/c] = (c/c)[t,E] = [t,E] = -iћη⁰⁰ = -iћ

[t,E] = -iћ

*Note* In this version the "canonical" commutation relation is derived from standard SR 4-Vector mathematics.
It doesn't require an axiom for its existence.
===
(*) As a component of the wave equations and probability currents in relativistic quantum mechanics
[(∂^μ∂_μ) + (m_oc/ћ)²]ψ = 0: Klein-Gordon RWE for free spin-0 particles
[(iγ^μ∂_μ) - (m_oc/ћ)]ψ = 0: Dirac RWE for free spin-1/2 particles
where {γ^μ,γ^ν} = γ^μγ^ν + γνγ^μ = 2 η^μνI₄
and (i/2)[γ_μ,γ_ν] =Σ_μν: The Relativistic Spin Matrices, see RQM section of Pauli Matrices

(∂·J = 0) **This applies to any kind of conserved 4-CurrentDensity** (an EM charge, a probablity charge, etc.)
J_prob = (iћ/2m_o)( ψ* ∂[ψ] - ∂[ψ*] ψ ) - (q/m_o)A(ψ*ψ)
J_charge = qJ_prob
J_charge = (iћq/2m_o)( ψ* ∂[ψ] - ∂[ψ*] ψ ) - (q²/m_o)A(ψ*ψ)
===
(*) As a key component in deriving QM from SR
U·U = (c)²
P·P = (m_oc)²
K·K = (m_oc/ћ)² = (ω_o/c)²
∂·∂ = (-im_oc/ћ)² = -(m_oc/ћ)² = -(ω_o/c)²
where is the last is the fundamental quantum equation
∂·∂ + (m_oc/ћ)² = 0

Full Equation (un-gauged)	Lorenz Gauge (∂·A = 0)	Field Type
	(∂·∂ + (m_oc/ћ)² )Ψ = 0	Ψ is a scalar, Klein-Gordon eqn for massive spin-0 field
	(∂·∂ + (m_oc/ћ)² )A = 0	A is a 4-Vector, Proca eqn for massive spin-1 field
	(∂·∂)Ψ = 0	Ψ is a scalar, Free-wave eqn for massless (m_o = 0) spin-0 field
∂_νF^νμ = 0^μ ∂_ν(∂^νA^μ - ∂^μA^ν) = 0^μ ∂_ν∂^νA^μ - ∂^μ∂_νA^ν = 0^μ (∂·∂)A^μ - ∂^μ(∂·A) = 0^μ	(∂·∂)A = Z (∂·∂)A^μ = 0^μ	A is a 4-Vector, Maxwell eqn for massless (m_o = 0) spin-1 field, no current sources
	(∂·∂)A = μ_oJ = ρ_oμ_oU = qn_oμ_oU = qμ_oN	A is a 4-Vector, Maxwell eqn for massless (m_o = 0) spin-1 field, current source J
∂_νF^νμ = qΨ ̅ γ^μΨ ∂_ν(∂^νA^μ - ∂^μA^ν) = qΨ ̅ γ^μΨ ∂_ν∂^νA^μ - ∂^μ∂_νA^ν = qΨ ̅ γ^μΨ (∂·∂)A^μ - ∂^μ(∂·A) = qΨ ̅ γ^μΨ	(∂·∂)A = qΨ ̅ γΨ (∂·∂)A^μ = qΨ ̅ γ^μΨ	QED, A is a 4-Vector, spin-1 field, current source Ψ ̅ γ^μΨ
	(∂·∂)h_TT^μν = 0^μν	Gravitational Waves, h_TT^μν is a (T)ranverse (T)raceless 2-Tensor representing gravitational radiation in the weak-field limit far from the source

(*) As a component of the RQM Covariant Derivative (internal particle spaces)
In modern elementary particle physics, one can define a gauge covariant derivative.
The full covariant derivative for the fundamental interactions of the Standard Model that we are presently aware of is:
∂_T^μ = ∂^μ -i (g₁)(Y/2)B^μ -i (g₂)(τ_j/2)·W_j^μ -i (g₃)(λ_a/2)·G_a^μ
∂_T = ∂ -i (g₁)(Y/2)B -i (g₂)(τ_j/2)·W_j -i (g₃)(λ_a/2)·G_a
It turns out there are several "internal particle spaces", of which EM is just one kind.
EM = Internal Paritcle Space U(1) Invariance, with (1) spin-1 gauge boson field B^μ
Weak = Internal Particle Space SU(2) Invariance with (3) spin-1 gauge boson fields W_j^μ, {j = 1..3}
Color = Internal Particle Space SU(3) Invariance with (8) spin-1 gauge boson fields G_a^μ, {a = 1..8}
The coupling constants (g₁,g₂,g₃) are arbitrary numbers that must be discovered from experiment.
Howerver, once they are found in one representation, they are fixed for all representations.
All of these internal particle spaces have been discovered empirically.
The ∂ itself is the field for SpaceTime invariance.
=============================

SRQM 4-Vector : Four-Vector Aharonov-Bohm Effect Diagram

SRQM 4-Vector Aharonov-Bohm Effect Diagram

Re-visiting the 4-TotalMomentum and 4-TotalWaveVector,
inc.
Internal Particle Spaces,
the Aharonov-Bohm Effect, the Josephson Effect, the Quantum Hall Effect,
the Magnetic Flux Quantum, the Conductance Quantum, etc. :

4-TotalMomentum P_T = (E_T/c,p_T) = (H/c,p_T) = (E/c + qφ/c,p + qa)
4-TotalWaveVector K_T = (ω_T/c,k_T) = (H,p_T) = (E/c + qφ/c,p + qa)
P_T = P + Q = P + qA
gives the Total Energy-Momentum content of an SR particle plus the SR field it is in: SI Units [kg·m/s].
H is the Hamiltonian Total energy ( = Total temporal momentum) of the event and p_T is the Total spatial momentum.
The Lorentz Scalar Product P_T·P_T = (H/c,p_T)·(H/c,p_T) = (H/c)² - p_T·p_T = (H_o/c)²
When the spatial part p_T is 0, this gives a Lorentz invariant rest Hamiltonian H_o.
Relativistic Hamiltonian H = γH_o
The 4-TotalMomentum of a system can be split into the 4-Momentum of a Particle + a charge (q) times a 4-VectorPotential.
Essentially, we are examining a lone particle running around in a big field/potential which can affect the particle.
Both the particle and the field have 4-Momentum, and it is the sum of all 4-Momentuṁs that is conserved.
This is used to derive the Classical EM laws.
The Conservation of 4-Momentum unites the Conservation of Energy and Conservation of 3-momentum into a single law,
and plays a major role in just about all physical effects.
S = -(P_T·R) and ∂[S] = -P_T.
Getting into Relativistic Analytic Mechanics, we can define an Action(S) as the negative Lorentz Scalar product of the 4-TotalMomentum with the 4-Position,
or the 4-TotalMomentum is the negative 4-Gradient of the Action.

Now, what if there are other types of covariant 4-VectorPotentials besides EM?
It turns out there are several "internal particle spaces", of which EM is just one kind.
EM = Internal Paritcle Space U(1) Invariance, with (1) spin-1 gauge boson field B^μ
Weak = Internal Particle Space SU(2) Invariance with (3) spin-1 gauge boson fields W_j^μ, {j = 1..3}
Color = Internal Particle Space SU(3) Invariance with (8) spin-1 gauge boson fields G_a^μ, {a = 1..8}
The coupling constants (g1,g2,g3) are arbitrary numbers that must be discovered from experiment.
Howerver, once they are found in one representation, they are fixed for all representations.
P_T = P + qA
K_T = K + (q/ћ)A
K_T = K + (g₁)(Y/2)B + (g₂)(τ_j/2)·W_j + (g₃)(λ_a/2)·G_a
-iK_T = -iK -i(g₁)(Y/2)B -i(g₂)(τ_j/2)·W_j -i(g₃)(λ_a/2)·G_a
∂_T = ∂ -i(g₁)(Y/2)B -i(g₂)(τ_j/2)·W_j -i(g₃)(λ_a/2)·G_aNow let's examine some quantum potential effects
4-VectorPotential A = (φ/c,a) = A[X] = A[(ct,x)] = (φ[(ct,x)]/c,a[(ct,x)]), often used as A_EM
P_T = P + qA + P_geo
K_T = K + (q/ћ)A + K_geo
K_T·X = K·X + (q/ћ)A·X + K_geo·X
-Φ_T = -Φ + (q/ћ)A·X - Φ_geo
Φ_T = Φ - (q/ћ)A·X + Φ_geo
Φ_T = Φ + Φ_pot + Φ_geo
The total phase (Φ_T) is:
the standard particle/wave phase (Φ)
plus the effects of the EM 4-VectorPotential phase (Φ_pot)
plus the effects of the Geometric Phase /Berry Phase (Φ_geo), which looks like a GR curvature effect.

The EM 4-VectorPotential part gives the Aharonov-Bohm Effect. There is a related effect called the Aharonov-Casher Effect which involves the magnetic moment.
Φ_pot = - (q/ћ)A·X
or taking a path...
dΦ_pot = - (q/ћ)A·dX
ΔΦ_pot = ∫_pathdΦ_pot = -(q/ћ)∫_pathA·dX = -(q/ћ)∫_path[(φ/c)(cdt) - a·dx] = -(q/ћ)∫_path(φdt - a·dx)
Note that both the Electric and Magnetic effects come out by using the 4-Vector notation
Electric AB effect: ΔΦ_potElec = - (q/ћ)∫_path(φdt)
Magnetic AB effect: ΔΦ_potMag = + (q/ћ)∫_path(a·dx)

The magnetic flux is defined as: Φ_B = ∮_loop(a·dx), the amount of flux going thru a closed loop.

*Note* This has an unfortunate notational clash.
Remember, in all other contexts Φ is a phase, with SI units of [rad]
Here, Φ_B is a magnetic flux with SI units of [Wb = (kg·m²) /(s²·A) = (kg·m²) /(s·C)]

Then ΔΦ_potMag = (q/ћ)∫_path(a·dx) → (q/ћ)∮_loop(a·dx) = (q/ћ)Φ_B
Now, examine the case change in phase is a multiple of 2π, and when the charge q = 2e, a Cooper-Pair of electrons.
ΔΦ_potMag = n2π = (2e/ћ)∫_path(a·dx) = (2e/ћ)Φ_B
Φ_B = n2π(ћ/2e) = nh/2e
and taking the case for a single loop, n = 1
Φ₀ = h/2e, which is the magnetic flux quantum, which is found in the Josephson Effect.
1/Φ₀ = 2e/h is the Josephson Constant
see Little-Parks Effect, Macroscopic Quantum Phenomena,

SRQM 4-Vector : Four-Vector Josephson Junction Effect Diagram

SRQM 4-Vector : Four-Vector Josephson Junction Effect Diagram

Let's go a bit further...
Φ_pot = -(q/ћ)A·X
Let A be constant.
d/dτ[Φ_pot] = d/dτ[-(q/ћ)A·X] = -(q/ћ)d/dτ[A·X] = -(q/ћ) (d/dτ[A]·X + A·d/dτ[X]) = -(q/ћ) ( 0 + A·U)
A·U = -(ћ/q)d/dτ[Φ_pot], where (A·U) is the Rest Electric Potential
φ_o = V_o = -(ћ/q)d/dτ[Φ_pot]
γφ_o = γV_o = -(ћ/q)γd/dτ[Φ_pot]
φ = V = -(ћ/q)γd/dτ[Φ_pot]
φ = V = -(ћ/q)γ²d/dt[Φ_pot]
Taking the low-velocity limiting-case
φ = V ~ -(ћ/q)d/dt[Φ_pot]
And taking again a Cooper-pair, q = -2e
φ = V ~ (ћ/2e)d/dt[Φ_pot], which is the Superconducting Phase Evolution Equation for a Josephson Junction, the Josephson Effect.

Now then, the "potential" doesn't have to be Electromagnetic in origin.
Remember,
Φ_T = Φ + Φ_pot + Φ_geo
The total phase (Φ_T) is:
the standard particle/wave phase (Φ)
plus the effects of the EM 4-VectorPotential phase (Φ_pot)
plus the effects of the Geometric Phase /Berry Phase (Φ_geo), which looks like a GR curvature effect.

see
Force-Free Gravitational Redshift: Proposed Gravitational Aharonov-Bohm experiment,
A Gravitational Aharonov-Bohm Effect, and its Connection to Parametric Oscillators and Gravitational Radiation,
Gravitational Aharonov-Bohm effect,

SRQM 4-Vector : Four-Vector Hamilton-Jacobi vs Action, Josephson vs Aharonov-Bohm Diagram

Four-Vector Hamilton-Jacobi vs Action, Josephson vs Aharonov-Bohm Diagram

=============================
Now let's examine another Lorentz Scalar Invariant:
P_T = P + qA
Introduce the 4-CyclicWaveVector K_c = K/2π
Let's set the 4-TotalMomentum to 4-Zero
P_T = P + qA = 0
Then
P = - qA
ћK = - qA
h K_cyc = - qA
K_cyc = - (q/h)A

Now, let's dot it with the 4-CurrentDensity
J = ρ_oU = n_oqU

K_cyc·J = - (q/h)A·n_oqU
K_cyc·J = - (n_oq²/h)A·U = - (n_oq²/h)(φ_o), where (φ_o) is the electric potential.

So: (K_cyc·J)/(A·U) = - (n_oq²/h)
If we are dealing with individual particles, we can use a delta function n_o ~ δ(X - X')
If there is a spin degeneracy of 2 for the electron, which has a charge q = -e

(K_cyc·J)/(A·U) = - δ(X - X')(2e²/h)

Identify G₀ = (2e²/h) as a unit of quantum conductance, which can appear in a quantum point contact.
This leads to the Quantum Hall Effect.
R_K = 2/G₀ = (h/e²) is the Von Klitzing Constant

Now then, the two effects combined lead to the operational principles of the Watt Balance.
=============================

Re-visiting the Stress-Energy Tensor :
Stress-Energy Tensors T^μν: Symmetric
T_GRvacuum^μν = 0
T_{relativisticfluid}^μν = (ρ_eo)V^μν - (p_o)H^μν + (T^μQ^ν + Q^μT^ν) + Π^μν
T_perfectfluid^μν = (ρ_eo + p_o)U^μU^ν/c² - (p_o)η^μν = (ρ_eo + p_o)T^μT^ν - (p_o)η^μν = (ρ_eo)T^μT^ν - (p_o)H^μν = (ρ_eo)V^μν - (p_o)H^μν
   T_dust^μν = (ρ_eo)U^μU^ν/c² = (ρ_eo)T^μT^ν = (ρ_eo)V^μν
   T_vacuum^μν = -(p_o)η^μν = (ρ_eo)η^μν
   T_{radiation = nulldust}^μν = p_o(4U^μU^ν/c² - η^μν) = p_o(4T^μT^ν - η^μν) = p_o(4V^μν - η^μν) = (ρ_eo)[V^μν - (1/3)H^μν] = (ρ_eo)N^μν
T_{EM = photongas}^μν = (1/μ_o)(F^μαη_αβF^νβ - η^μνF_δγF^δγ/4)
gives the Energy-Momentum content of an SR particle at a particular event: SI Units [kg·m/s].

We can now add one for the Klein-Gordon Equation.
T_Klein-Gordon^μν = (ћ²/m)( η^μα η^νβ + η^μβ η^να - η^μν η^αβ )∂_αΨ̅ ∂_βΨ - η^μν mc² Ψ̅ Ψ

=============================

Crystal Momentum :
The formula for Quantum Crystal Momentum comes from the relativistic formulation.
∂_X[K·X] = K
∂_K[K·X] = X

from the de Broglie relations, we get the Fourier transforms
∂_X = -iK
∂_K = iX

Example of relativistic crystal momentum velocity definition:
U = (1/ћ)∂_K[P·U]

First, prove that this is true:
(1/ћ)∂_K[P·U]
= ∂_K[K·U]
= ∂_K[(ω/c,k)·γ(c,u)]
= ∂_K[γ(ω - k·u)]
= γ ∂_K[(ω - k·u)]
= γ(c∂_ω, -∇_k)[(ω - k·u)]
= γ(c∂_ω[(ω - k·u)], -∇_k[(ω - k·u)])
= γ(c∂_ω[ω], -∇_k[- k·u])
= γ(c∂_ω[ω], +∇_k[k·u])
= γ(c,u)
= U

Next, the part in the function
P₁·U₂ = γ[u₂](E- p₁·u₂) = E_rel

U = (1/ћ)∂_K[P·U] = (1/ћ)∂_K[E_rel]
U = γ(c,u) = (1/ћ)(c∂_ω, -∇_k)[E_rel]

Take the spatial part:
γ(c,u) = (1/ћ)(c∂_ω, -∇_k)[E_rel]
γu = (1/ћ)(-∇_k)[E_rel]

Take the Newtonian limit:
u = (1/ћ)(-∇_k)[E_rel]
This is the quantum formula for crystal momentum.
=============================

Resolution of the EPR Paradox :
see EPR Paradox, Bell's Theorem, Bell State, Bell Test Experiments, Kochen-Specker Theorem,
see Interpretations of Quantum Mechanics, Quantum Entanglement, Counterfactual Definiteness,
see Relational Quantum Mechanics,
The EPR paradox does not refute Heisenberg Uncertainty, nor the Principle of Locality, nor realism.
The EPR paradox is about the relation of measurements to properties being measured.
In the SRQM Interpretation, it shows that particles *CAN* have simultaneous properties, which are local and real.
As stated before, the Heisenberg Uncertainty Principle is about the non-commutative properties of the Minkowski Metric with regard to sequential measurement acts.
This commutator has to do with the order of the operations/measurements on a single particle/event, which indicates timelike intervals, not spacelike intervals.

Thus, it makes no statement about whether a given event's "properties" can be simultaneous or not.
It does make a statement about the effects of "sequential measurements" along the timelike intervals of individual worldlines.

In the EPR Paradox:
The observer correlates particles A and B at some local SpaceTime event, and then allows them to space-like separate onto their own individual worldlines.
At the point of correlation, the particles have identically opposite ket vectors due to conservation laws. (P) + (-P) = 0. Conservation of property P.
Each particle has its own ket vector with respect to a given observer.
It is a simply an informational state, and can be different for different observers who have different informational states.
A measurement act on one particle does *NOT* affect the other space-like separated particle.
Even though they may share the same informationally correlated state, the measurement on A has no instantaneous effect on B, or vice-versa.
The only thing that happens is that the correlated state is (usually) removed from the particle under observation due to the measurement act.
In fact, there are some possible observers who see event A before B, some who see A simultaneous with B, and some who see A after B.
The measurement of one cannot have any operational effect on the other, as this would violate the rules of SR, and we have shown above that QM is directly derivable from SR.

Thus, the EPR Paradox does indeed prove Einstein correct, that a particle does have simultaneous properties.
The interesting fact of nature is that apparently only certain commuting properties can be simulatenously measured on the same particle.
The Heisenberg Uncertainty is about sequential measurements along individual worldlines.

Bell's Theorem,
Bell's theorem, named after John Stewart Bell, is a ‘no-go theorem’ that draws an important distinction between quantum mechanics (QM) and the world as described by classical mechanics. In its simplest form, Bell's theorem states: No physical theory of local hidden variables (consistent with local realism or possibly counter-factual definiteness) can ever reproduce all of the predictions of quantum mechanics.

Right! SR is not a theory of local hidden variables. We have already shown that SR leads directly to RQM, and thence to QM in the low-velocity limit.
The SRQM Interpretation says that QM is derivable from SR. Hence, it does not ascribe any primacy to Classical Mechanics.
CM is both a low-velocity limit and a non-quantum limit (meaning the limit in which changes of a few quanta have a negligible effect on the overall system).

A mistake that many scientists make is to assume that the fault is in locality, and think that QM is somehow non-local.
That is incorrect. Relativity is all about locality. The problem is in measurement theory. What exactly is a measurement? A measurement is a way of getting information about a particle's state.
The trick is that there is physically no way to arrange a measuring system such that it can measure non-commuting properties in a single interaction for a single particle.
The properties are always there, we just can't measure both at the same instant, and the measurement of one will alter the other if it is non-commuting.
The limitation is in the ability to simultaneously measure, not in the particle's properties.

Kochen-Specker Theorem,
In quantum mechanics, the Kochen-Specker (KS) theorem, also known as the Bell-Kochen-Specker theorem, is a "no go" theorem proved by John S. Bell in 1966 and by Simon B. Kochen and Ernst Specker in 1967. It places certain constraints on the permissible types of hidden variable theories which try to explain the apparent randomness of quantum mechanics as a deterministic model featuring hidden states. The version of the theorem proved by Kochen and Specker also gave an explicit example for this constraint in terms of a finite number of state vectors. The theorem is a complement to Bell's theorem. The theorem proves that there is a contradiction between two basic assumptions of the hidden variable theories intended to reproduce the results of quantum mechanics: that all hidden variables corresponding to quantum mechanical observables have definite values at any given time, and that the values of those variables are intrinsic and independent of the device used to measure them. The contradiction is caused by the fact that quantum mechanical observables need not be commutative. It turns out to be impossible to simultaneously embed all the commuting subalgebras of the algebra of these observables in one commutative algebra, assumed to represent the classical structure of the hidden variables theory, if the Hilbert space dimension is at least three. The Kochen–Specker proof demonstrates the impossibility that quantum mechanical observables represent "elements of physical reality". More specifically, the theorem excludes hidden variable theories that require elements of physical reality to be non-contextual (i.e. independent of the measurement arrangement). As succinctly worded by Isham and Butterfield, the Kochen–Specker theorem "asserts the impossibility of assigning values to all physical quantities whilst, at the same time, preserving the functional relations between them."

Right! A particle can simultaneously have a full set of properties. It is, however, impossible to simultaneously measure non-commuting properties: meaning that there is physically no way to setup an arrangement of atoms such that the interaction of the particle with the arrangement allows simultaneous information about non-commuting properties. The theorem is about the measuring arrangement, not the particle.
=============================

Wavefunction Collapse and the Measurement Problem :
see Relational Quantum Mechanics, WaveFunction Collapse, Measurement Problem, Measurement in QM,
Based on everything we know so far, we need to reassess the idea of the wavefunction collapse.
The Copenhagen View is simply wrong wrt. a physical state actually collapsing, and wrt. a quantum state interacting with a classical state.
If, however, one is referring to one's information about a state, then OK.
Everything is relativistic, and since we derived quantum features from SR, everything is thus quantum.
There is no reason to suppose an artificial separation between micro and macroscopic objects.
SR shows us that space-like separated particles may be encountered in any temporal order, A before B, A simultaneous with B, A after B.
Thus, a Measurement Act cannot have a causal influence on another particle that is on the outside of its local lightcone.
If it did, one gets into all kinds of temporal paradoxes.
This, along with EPR experiments, indicate that the Quantum Wavefunction is a "State of Information about a Physical System",
and not the "Physical State of a System" itself.
One observer's information about the system may be different from another observer's information about a system.
The thing that ties everything together are the properties of Relativity.
For instance, a particle has no absolute 3-velocity. There is only the 3-velocity relative to an observer.
And different observers will note different relative 3-velocities.
However, SR gives the answer: The invariant object known as the 4-Velocity.
Each particle has a 4-Position and 4-Velocity at each point along its worldline.
The components of these as seen by different observers will vary, according to the Lorentz transformations.

Another great example is Schrödinger's Cat.
However, let's add another human observer (suitably protected) in the box with the cat.
The inside observer can see whether the cat is (|Ψ> = |alive> or |Ψ> = |dead>), and calculates an informational wavefunction that reflects this.
The outside observer cannot, and thus has a different wavefunction which is the superposition (|Ψ> = |alive>+|dead>) that we all hear about.
The cat dies when hit with the operator (O = |dead><alive|), which occurs at some random time.
When the cat dies, the informational wavefunction "collapses" for the internal observer, in that it changes from definitely |Ψ> = |alive> to definitely |Ψ> = |dead>.
The outside observer's informational wavefunction however, remains unchanged until the box is opened, at which point it then informationally "collapses".
It goes from the superposition state to either definitely alive if the cat is still alive at the time or to definitely dead if the cat has died.
Also, consider the state for when the cat is alive when the box is opened.
It is in a definite state of alive. Each time the box is closed the state then "collapses" to the superposition of alive-dead for the outside observer.
The wavefunctions are not physical states - they are states of an observer's information about a physical system.
Thus, they reflect the "relative" knowledge of each observer wrt. the system in question.
The act of Measurement affects only the relationship with a given observer and the system in question, not any other nonlocal system or nonlocal observer.
Again, each particle's wavefunction is separate from any other particle's wavefunction.
The wavefunction is only the state of information about a system that stays with an observer.
In the EPR system, the two particles get a "correlated/entangled" state due to conservation laws.
The particles are then separated.
They retain separately their "correlated/entangled" states for the observers.
When the close-by observer measures the close-by particle, that observer/particle wavefunction both physically changes and informationally collapses.
Also, the informational state of the faraway particle collapses for the close-by observer, but its physical state does not change.
The informational states of both particles remain unchanged for the faraway observer until the faraway particle is measured,
or until he receives a signal with the true informational state of the close-by particle.

So, to recap:
A quantum particle only changes it's physical state upon interaction with another particle.
Changes in physical state are governed by SR Conservation Laws, in the form of entanglement.
A measurement is a way for an observer to get information about a particle's state, and generally changes the particle's state in some manner in the non-commuting variable.
A wavefunction is the informational state of knowledge about a particle or system of particles.
Different observers may have different informational states about the same particle, depending on the event of interaction with the particle.
Wavefunction "collapse" is an instantaneous change in the state of information about a particle, ie. a deduction.
Wavefunction "collapse" can occur when information is transferred, and does not physically affect the particles in question.
Deduction can be instantaneous, and hence, non-local, without violating relativistic laws.
Actual information transfer is limited by relativity, the speed-of-light.
A particle always has its full set of properties.
There is a physical limitation on the types of measurements that can be made to simultaneously measure those properties.
Commuting properties can be simultaneously measured on a single particle, non-commuting properties cannot be simultaneously measured on a single particle.
The EPR experiment gives a way to deduce a non-commuting property without actually doing a measurement.
This is allowed because it doesn't break the rule about being able to actually do two seperate measurements simultaneously on the "same" particle.
=============================

The Nature of Duality :
Duality has to date been presented as a mysterious quantum phenomena.
It is actually just the consequence of some simple 4-Vector math.
4-Position X = (ct,x) → (ct,x,y,z) SI Units [m]
4-WaveVector K = (ω/c,k) → (ω/c,k_x,k_y,k_z) SI Units [rad/m]

4-Differential dX = (cdt,dx) SI Units [m]
4-WaveVectorDifferential dK = (ω/c,dk) SI Units [rad/m]

4-Gradient ∂ = ∂_X = (∂_t/c,-∇) = (∂_t/c,- del) → (∂_t/c, -∂_x, -∂_y,-∂_z) = (∂/c∂t,-∂/∂x,-∂/∂y,-∂/∂z) SI Units [1/m]
4-WaveGradient ∂_K = (c∂_ω,-∇_k) = (c∂_ω,- del_k) → (c∂_ω, -∂_kx, -∂_ky,-∂_kz) = (c∂/∂ω,-∂/∂k_x,-∂/∂k_y,-∂/∂k_z) SI Units [m/rad]

K·X = (ω/c,k)·(ct,x) = (ωt - k·x) = -Φ
The Phase Φ of an SR Wave (represented by the 4-WaveVector K) is a Lorentz Scalar.

K = -∂_X[Φ]
X = -∂_K[Φ]

d⁴X = -(V_Xo)dT·dX = cdt d³x = cdt dx dy dz
The 4D coords that are integrated to give a 4D Position Volume
d⁴K = (V_Ko)dT·dK = (dω/c) d³k = (dω/c) dk_xdk_ydk_z
The 4D WaveVector coords that are integrated to give a 4D WaveVector Volume

d³kd³x = (V_Ko)dT·(-V_o)dT = ( -V_o V_Ko)dT·dT

[∂_X,X] = η^μν = Minkowski Metric, and thus inherently a non-zero commutation relation
[∂_K,K] = η^μν = Minkowski Metric, and thus inherently a non-zero commutation relation

K = i ∂_X{in the standard convention}
∂_X = ±i K{for f = ae^±i(K·X), g = f* = ae^∓i(K·X)}

∂_X = ±iK

[∂_X,X] = η^μν = [∂_K,K]
[∂_X,X] = [∂_K,K]
[∂_X,X] = -[K,∂_K]
[±i K,X] = -[K,∂_K]
±i[K,X] = -[K,∂_K]
±i²[K,X] = -i[K,∂_K]
±(-1)[K,X] = -i[K,∂_K]
±[K,X] = i[K,∂_K]
[K,X] = ±i[K,∂_K]
[K,X] = [K,±i∂_K]

X = ±i∂_K
∂_K = ∓iX

∂_X = ±iK{for f = ae^±i(K·X), g = f* = ae^∓i(K·X)}
∂_K = ∓iX{for f = ae^±i(K·X), g = f* = ae^∓i(K·X)}

Thus ∂_X[f] = ±iKf at the same time ∂_K[g] = ∓iXg
or ∂_X[f] = ±iKf at the same time ∂_K[f*] = ∓iXf*

Basically:
The X-space operator acts on wavefunction (f)
The K-space operator acts on wavefunction (f*), the dual of (f)
Since these were generated from our 4-Vector formalism, these are Lorentz Invariant.

For light rays, we have K·K → 0. {This applies only to massless particles/waves, they are 4-Null}
∂[K·K] = 2*K·∂[K] = ∂[0] = Z.
d²X/dθ² = dK/dθ = (K·∂)[K] = K·∂[K] = 0
So, these light rays are straight, in both 3D and 4D. See Rindler, Intro to SR, 2nd Ed., pg. 63.

dX/dτ = (U·∂)[X] = U	dX/dθ = (K·∂)[X] = K
U·U = c² U₁·U₂ = (γ₁₂)c² U·U_o = (γ_rel)c²	K·K = (ω_o/c)²
∂[U·U] = 2*U·∂[U] = ∂[c²] = Z ∂[U₁·U₂] = U₁·∂[U₂] +U₂·∂[U₁] = ∂[(γ₁₂)c²] = c² ∂[γ₁₂] ∂[U·U_o] = U·∂[U_o] +U_o·∂[U] = (0) +U_o·∂[U] = ∂[(γ_rel)c²] = c² ∂[γ_rel]	∂[K·K] = 2* K·∂[K] = ∂[(ω_o/c)²] = Z, if ω_o is constant
d/dτ[U·U] = 2U·d/dτ[U] = 2U·A = d/dτ[c²] = 0 d/dτ[U₁·U₂] = U₁·d/dτ[U₂] +U₂·d/dτ[U₁] = U₁·A₂ +U₂·A₁ = d/dτ[(γ₁₂)c²] = c²d/dτ[γ₁₂] d/dτ[U·U_o] = U·d/dτ[U_o] +U_o·d/dτ[U] = (0) +U_o·A = d/dτ[(γ_rel)c²] = c²d/dτ[γ_rel]
d² X/dτ² = dU/dτ = ? = (U·∂)[U] = U·∂[U] = Z but should be A instead try d² X/dτ² = dU/dτ = (U_o·∂)[U] = U_o·∂[U] = A = ? = c² ∂[γ_rel]	d² X/dθ² = dK/dθ = (K·∂)[K] = K·∂[K] = 0 ?

Ah, must be careful, another one where tensor index notation required
U·∂[U] is actually U^μη_μν∂^νU^σ
They are differently indexed U's
see also Englert-Greenberger-Yasin duality relation, Complementarity,
=============================

Quantum Mysteries :
There are a number of mysterious quantum effects which might now have reasonable and logical explanations:

Hypotreatise: All mysterious quantum phenomena which up till now have been attributed simply to the axiomatic weirdness of quantum mechanics are in fact manifestations of relativistic effects.
A couple that come to mind are radioactive decay with its associated half-life rule, and quantum tunneling.

Let's examine quantum radioactive decay:
A macroscopic sample of a pure substance, meaning all the atoms should be identical, has a "half-life", whereby approximately half of the sample decays into new products within a specified timeframe. Another half of the remaining will again have decayed in the next specified time-frame, and so on and so on. The question is why does it occur this way. If all of the atoms are identical, why don't they all decay at the same time?

Special Relativity to the rescue...

Consider the twin paradox of relativity. Two individuals start at event A with identical ages. One individual takes a trip while one remains at rest. At some future point the individual that had left returns to the the one at rest at event B. There is a difference in the ages of the two individuals. While paradoxical, the mathematics behind the difference in aging is fully explained by relativistic laws. It is only a paradox if you consider to all particles age at the same rate. Relativity tells us that particles on separate worldlines age according to their own clocks, and that the actual path taken through SpaceTime determines the age difference upon the reuniting of the particles.

Now, back to the radioactive sample. Each atom, indeed each subatomic particle is cruising along on its own worldline. As the particles "jiggle around" one another, there will be differences in the aging rates due to the twin paradox. Two particles initially at the same age at event A (in phase with each other) with be at different ages at event B, thus leading to states in which the system is no longer "in-sync" or "in-phase", so to speak. This could be the physical reason why the atom then undergoes spontaneous decay.

Now, consider a bunch of particles in the sample. There will be some distribution of ages that build up as the entire sample "ages", with each individual part of it aging at slightly different rates. Those that get "out-of-sync" undergo spontaneous decay. I propose that the distribution is that of the half-life rule. I will attempt to prove this mathematically at some point, but for now it's just a hypotreatise.

Consider also that the difference in half-life rates may be a function of "how relativistic" the individual particles get. Those with large relativistic velocities may get "out-of-sync" more quickly, and thus have shorter half-lives. This will have to be examined.

Quantum tunneling is the idea that a particle can enter a region that is "classically" forbidden due to energy conservation ideas.
However, with relativistic effects available, this gives a few more options, like the ability of a particle to trade off energy & momentum with a potential field, via minimal coupling.

Let's summarize a bit:
We used the following relations: (particle/location→movement/velocity→mass/momentum→wave duality→SpaceTime structure)
With the exception of 4-Velocity being the derivative of 4-Position, all of these relations are just constants times other 4-Vectors.

R = (ct,r)	particle/location
U = dR/dτ	movement/velocity
P = m_oU	mass/momentum
K = (1/ћ)P	wave/particle duality
∂ = -iK	SpaceTime/wave structure

(c) connects the time dimension to the space dimensions
(ћ) connects the light-cone boundary (massless photonic behavior) to the light-cone interior (massive particle behavior)
(i) connects wave to particle

By applying the Scalar Product law to these relations, we get:
U·U = (c)²
P·P = (m_oc)²
K·K = (m_oc/ћ)²
∂·∂ = (-im_oc/ћ)² = -(m_oc/ћ)²

∂_t²/c² = ∇·∇ - (m_oc/ћ)²

This is the RQM Klein-Gordon Relativistic Wave Eqn (derived from SR with no QM axioms assumed)

=====================================================================
*********************************************************************
=====================================================================

Ok, now let's recap again...
We have now looked the [SR→QM] formulas individually,
but let's examine them all together to notice similarities and differences.
They are really very very similar to the Standard SR formulae.
Note also that all of these formula are Tensor equations, and therefore manifestly covariant,
meaning that they are all valid for all inertial observers, no matter what coordinates they may be using.

=====================================================================
*********************************************************************
=====================================================================

P = ћK
This is the SR 4-Vector version of the Planck-Einstein relation and de Broglie Matter-Wave relation.

∂ = -iK{for f = ae^-i(K·X)}
The SR Plane-Wave Equation
Operator Formalism : [∂] = -iK
Unitary Evolution : ∂ = [-i]K
Wave Structure : ∂ = -i[K]

P = iћ∂
The Schrödinger QM Relations.
The temporal eqn. is { E = iћ∂_t}, the Schrödinger QM Energy Relation.
The spatial eqn. is { p = -iћ∇}, the Schrödinger QM 3-momentum Relations.

[∂^μ,X^ν] = η^μν = Minkowski Metric, and thus inherently a non-zero commutation relation
Standard SR 4-Vectors lead to Operator and Commutation Relations
[P^μ,X^ν] = iћη^μν
And the Standard QM Commutation Relation derived from the SR Relation makes a hell of lot more sense than the other way around.
[∂_K^μ,K^ν] = η^μν = Minkowski Metric
And the likewise for the Wave-vector version
∂_X = ±i K{for f = ae^±i(K·X), g = f* = ae^∓i(K·X)}
∂_K = ∓i X{for f = ae^±i(K·X), g = f* = ae^∓i(K·X)}
∂_X[f] = ±i Kf at the same time ∂_K[f*] = ∓i Xf*

[M^μν, M^ρσ] = iћ(η^νρM^μσ + η^μσM^νρ + η^σνM^ρμ + η^ρμM^σν)
[M^μν, P^ρ] = iћ(η^ρνP^μ - η^ρμP^ν)
And we get commutation relations for relativistic angular momentum

Form a chain of Lorentz Scalar Equations...
U·U = (c)²
P·P = (m_oc)²
K·K = (m_oc/ћ)² = (ω_o/c)²
∂·∂ = (-im_oc/ћ)² = -(m_oc/ћ)² = -(ω_o/c)²
The last is the Klein-Gordon Equation, the Relativistic Quantum Wave Equation for Spin-0 Particles.

(∂·∂ + (m_oc/ћ)² )Ψ = 0	Ψ is a scalar, Klein-Gordon eqn for massive spin-0 field
(∂·∂ + (m_oc/ћ)² )A = 0	A is a 4-Vector, Proca eqn for massive spin-1 field, Lorenz Gauge
(∂·∂)Ψ = 0	Ψ is a scalar, Free-wave eqn for massless (m_o = 0) spin-0 field
(∂·∂)A = 0	A is a 4-Vector, Maxwell eqn for massless (m_o = 0) spin-1 field, no current sources, Lorenz Gauge
(∂·∂)A = μ_oJ = ρ_oμ_oU = qn_oμ_oU = qμ_oN	A is a 4-Vector, Maxwell eqn for massless (m_o = 0) spin-1 field, current source 4-Vector J, Lorenz Gauge Classical EM, does not include effects of particle spin in the source J = ρ_oU
(∂·∂)A = μ_oJ = μ_oqΨ ̅ ΓΨ (∂·∂)A^ν = μ_oJ^ν = μ_oqΨ ̅ γ^νΨ	QED, A is a 4-Vector, Maxwell eqn for massless (m_o = 0) spin-1 field, current source Spinor J, Lorenz Gauge Quantum EM, does include effects of particle spin in the source J = qΨ ̅ γ^μΨ

∂_T^μ = ∂^μ - i(g₁)(Y/2)B^μ - i(g₂)(τ_j/2)·W_j^μ - i(g₃)(λ_a/2)·G_a^μ
∂_T = ∂ - i(g₁)(Y/2)B - i(g₂)(τ_j/2)·W_j - i(g₃)(λ_a/2)·G_a
The full covariant derivative for the fudamental interactions of the Standard Model that we are presently aware of is:

4-ProbabilityCurrentDensity J_prob = (iћ/2m_o)( ψ* ∂[ψ] - ∂[ψ*] ψ ) - (q/m_o)A(ψ*ψ)
4-NumberFlux = 4-NumberCurrentDensity = N = (nc,cu)
4-ChargeCurrentDensity J_charge = qJ_prob
The 4-ProbabilityCurrentDensity and 4-ChargeCurrentDensity.
The 4-ProbabilityCurrentDensity and the 4-NumberCurrentDensity (4-NumberFlux) are the same thing.

K·K = (ω_o/c)² = (1/cT_o)² = (m_oc/ћ)² = (1/λ_C)²
Re-examining the Lorentz Scalar Product of the 4-Wave Vector - The Compton Wavelength
This same constant appears in the Klein-Gordan RQM Equation.

Δλ = λ_C(1-cos[ø])
The Compton Effect

Φ_T = Φ_particle + Φ_pot + Φ_geo
K_T = K_particle + K_pot + K_geo
K_T = K_particle + -(q/ћ)A + K_geo
The 4-TotalWaveVector can be made of components including Particle de Broglie Matter-Waves, EM Interaction Waves (EM Potential), and Geometric (GR) Phase Waves.
This leads to a number of "quantum effects".

Φ_pot = - (q/ћ)A·X
dΦ_pot = - (q/ћ)A·dX
ΔΦ_pot = ∫_pathdΦ_pot = -(q/ћ)∫_pathA·dX = -(q/ћ)∫_path[(φ/c)(cdt) - a·dx] = -(q/ћ)∫_path(φdt - a·dx)
The Aharonov-Bohm Effect : Note that both the Electric and Magnetic effects come out by using the 4-Vector notation

Φ_pot = -(q/ћ)A·X
A·U = -(ћ/q)d/dτ[Φ_pot] = φ_o{for Aconstant}
φ = V ~ -(ћ/q)d/dt[Φ_pot]
φ = V ~ (ћ/2e)d/dt[Φ_pot], where q = -2e
Φ_B = n2π(ћ/2e) = nh/2e
and taking the case for a single loop, n = 1
Φ₀ = h/2e, which is the magnetic flux quantum, which is found in the Josephson Effect.
1/Φ₀ = 2e/h is the Josephson Constant
see Little-Parks Effect, Macroscopic Quantum Phenomena,

(K_cyc·J)/(A·U) = - (n_oq²/h)
(K_cyc·J)/(A·U) = - δ(X - X')(2e²/h)
Identify G₀ = (2e²/h) as a unit of quantum conductance, which can appear in a quantum point contact.
This leads to the Quantum Hall Effect.

P_T = P_particle + P_pot + P_geo
P_T = P + Q + P_geo
P_T = P + qA + P_geo
K_T = K + (q/ћ)A + K_geo
K_T·X = K·X + (q/ћ)A·X + K_geo·X
-Φ_T = -Φ + (q/ћ)A·X - Φ_geo
Φ_T = Φ - (q/ћ)A·X + Φ_geo
Φ_T = Φ + Φ_pot + Φ_geo
The 4-TotalMomentum has a component dependent on the 4-PotentialMomentum
When transformed to the 4-TotalWaveVector, the 4-PotentialWaveVector has an explicit factor of (ћ).
Likewise, the TotalPhase is a function of the regular SpaceTime phase + a "quantum" potential phase Φ_pot = - (q/ћ)A·X + a possible "quantum" geometric phase.

More SR Physical 4-Vectors

Going further,
Consider the following more comprehensive set of SR 4-Vectors:
========================================================================
4-Position R = (ct,r) → (ct,r,θ,z) or (ct,r,θ,φ); X = (ct,x) → (ct,x,y,z)
4-Velocity U = (U⁰,Uⁱ) = γ(c,u)
4-Acceleration A = (A⁰,Aⁱ) = γ(cγ̇,γ̇u + γu̇) = γ(cγ̇,γ̇u + γa)
4-Differential dR = (cdt,dr); dX = (cdt,dx)
4-Displacement ΔR = (cΔt,Δr); ΔX = (cΔt,Δx)
4-Momentum P = (E/c,p) = (mc,p)
4-MomentumDensity G = (E_den/c,p_den) = (u_e/c,g)
4-Force F = (F⁰,Fⁱ) = γ(Ė/c,ṗ) = γ(Ė/c,f) = γ(ṁc,f)
4-ForcePure F_p = γ(u·f/c,f)
4-Force_EMF_EM = γq( (u·e)/c, (e) + (u⨯b) )
4-ForceHeat F_h = γṁ(c,u) = γ²ṁ_o(c,u)
4-ForceScalar F_s = k(∂_t[Φ],-∇[Φ])
4-ForceDensity F_den = γ(Ė_den/c,f_den)
4-NumberFlux N = N_f = n(c,u) = (cn,nu) = (cn,n) = Σ_a[∫dτ δ⁽⁴⁾[X - X_a(τ)]dX_a/dτ]
4-EntropyFlux S = s(c,u) = (cs,su) = (cs,s)
4-CurrentDensity J = ρ(c,u) = (cρ,ρu) = (cρ,j)
4-VectorPotential A = (φ/c,a) = A[X] = A[(ct,x)] = (φ[(ct,x)]/c,a[(ct,x)]), often used for/as A_EM
4-PotentialMomentum Q = (U/c,q) = q(φ/c,a)
4-TotalMomentum P_T_particle = (E_T/c,p_T) = (H/c,p_T) = (E/c + U/c,p + q) = (E/c + qφ/c,p + qa), meaning the sum of particle momentum and charged interaction potential momentum
4-TotalMomentum P_T_sys = (E_T/c,p_T) = (H/c,p_T) = Σ_n[P_T_particle(n)], meaning that the total 4-Momentum of a system is the sum of all individual particle 4-Momenta in the system
4-WaveVector K = (ω/c,k) = (ω/c,n̂ω/v_phase) = (ω/c,ωu/c²) = (ω/c)(1,β) = (1/cT,n̂/λ)
4-CyclicWaveVector K_cyc = (ν/c,k_cyc) = (ν/c,n̂ν/v_phase) = (ν/c,νu/c²) = (ν/c)(1,β) = (1/cT,n̂/λ)
4-TotalWaveVector K_Tsys = (ω_T/c,k_T) = Σ_n[K_T_wave(n)], meaning that the total 4-WaveVector of a system is the sum of all the individual 4-WaveVectors in the system
4-DifferentialWaveVector dK = (dω/c,dk)
4-Gradient ∂ = ∂_X = (∂_t/c,-∇) = (∂_t/c,-del) → (∂_t/c, -∂_x, -∂_y,-∂_z) = (∂/c∂t,-∂/∂x,-∂/∂y,-∂/∂z)
4-WaveGradient ∂_K = (c∂_ω,-∇_k) = (c∂_ω,- del_k) → (c∂_ω, -∂_kx, -∂_ky,-∂_kz) = (c∂/∂ω,-∂/∂k_x,-∂/∂k_y,-∂/∂k_z)
4-Polarization Ε = (ε⁰,ε) → (ε·β,ε), with (ε·β = 0) *Note* this can have complex coefficients, and comes from standard EM theory (non-QM), see Jones Vector
I choose this particular set because each of these is considered a basic SR 4-Vector,
Adding a few more which I either haven't seen in the literature or were previously considered quantum mechanical
*****
4-TotalWaveVector K_T = (ω_T/c,k_T) = (ω/c + qφ/c + ω_geo,k + qa + k_geo), meaning the sum of particle wavevector and charged interaction and geometric Berry wave
4-MomentumGradient ∂_P = (c∂_E,-∇_p), which is just (ћ) times the 4-WaveGradient
4-MomentumIncSpin P_s = (p_s⁰,p_s) = (σ⁰E/c,σ·p) = ( σ⁰(E_T/c - qφ/c),σ·(p_T -qa) ) {can have complex components due to Pauli Spin Matrices}
4-ProbabilityCurrentDensity J_prob = (iћ/2m_o)( ψ* ∂[ψ] - ∂[ψ*] ψ ) - (q/m_o)A(ψ*ψ) {can have complex components}
4-ChargeCurrentDensity J_charge = qJ_prob
4-LatticePosition R_K = (ct_K,r_K)
====

The combination of a Lorentz Invariant Charge*4-VectorPotential leads to a 4-PotentialMomentum.
The 4-TotalMomentum = 4-Momentum + 4-PotentialMometum

Potentials/Fields:

Let's back up to the 4-Momentum equation. Momentum is not just a property of individual particles, but also of fields.
These fields can be described by 4-Vectors as well.
One such relativistically invariant field is the 4-VectorPotential A, which is itself a function of 4-Position X.
Typically, we deal with the Electromagnetic (EM) 4-VectorPotential, but it could be any kind of relativistic charge potential...
4-VectorPotential A[X] = A[(ct,x)] = (φ/c,a) = (φ[(ct,x)]/c,a[(ct,x)]), with the [(ct,x)] meaning it is a function of time t and position x.
While a particle exists as a worldline over SpaceTime, the 4-VectorPotential exists over all SpaceTime.
The 4-VectorPotential can carry energy and momentum, and interact with particles via their charge q.

PotentialMomentum:

One may obtain the PotentialMomentum 4-Vector by multiplying by a charge q, Q = qA
4-PotentialMomentum Q = qA = q(φ/c,a) = (U/c,q)
The 4-TotalMomentum is then given by P_T = P + Q
This includes the momentum of particle and field, and it is the locally conserved quantity.
4-TotalMomentum P_T = (H/c,p_T), for which these are the TotalEnergy = Hamiltonian and 3-totalMomentum.
P = P_T - Q = m_oU
Now working back, we can make our dynamic 4-Momentum more general, including the effects of potentials.
4-Momentum P = (E/c,p) = (H/c - U/c,p_T - p_EM) = (H/c - qφ/c,p_T - qa)
The dynamic 4-momentum of a particle thus now has a component due to the 4-VectorPotential,
and reverts back to the usual definition of 4-momentum in the case of zero 4-VectorPotential.
Likewise, following the same path as before...
K = P/ћ
4-WaveVector K = (ω_T/c - (q/ћ)Φ/c,k_T - (q/ћ)a)
∂ = -iK
4-Gradient ∂ = (∂_T/c∂t - (iq/ћ)Φ/c,-∇_T - (iq/ћ)a) = (∂_t/c,-∇)
Define 4-TotalGradient D = ∂ + iq/ћA
This is the concept of "Minimal Coupling"
Minimal Coupling can be extended all the way to non-Abelian gauge theories and can be used to write down all the interactions of the Standard Model of elementary particles physics between spin-1/2 "matter particles" and spin-1 "force particles"
Minimal Coupling applied to the Dirac Eqn. leads to the Spin Magnetic Moment-External Magnetic Field coupling W = -γ_eS·B, with γ_e = q_e/m_e, the gyromagnetic ratio.
The corrections to the anomalous magnetic moment come from minimal coupling applied to QED

In addition, we can go back to the velocity formula:

u = c²(p)/(E) = c²(p_T - qa)/(H - qΦ)

SpaceTime Lattice, Lorentz Invariant Quantization, Radial Standing-Wave Hypotreatise, Quantum Jumps, Angular Momentum

Let's examine an interesting lattice concept... see Reciprocal Lattice, Bravais Lattice, Pontryagin Duality,

4-LatticePosition R' = (ct',r')
4-WaveVector K = (ω/c,k) = (ω/c,n̂ω/v_phase) = (ω/c)(1,β) = (1/cT,n̂/λ) = (2π/cT,2π n̂/λ)
Let [(R'·K) = -n] with (n) as an integer.
Then [Δ(R'·K) = -Δn], with (n) and (Δn) as integers. This gives a Lorentz Invariant with magnitude in a spatial direction.
Then e^{[i2πΔ(R'·K)]} = e^[-i2πΔn] = 1, a unit phase factor for integer (Δn).
Let's see what happens based on this definition...

One can think of this as a particle with a particular wavevector (K).
There exists a series (Δn) of certain intervals (ΔR') based on this wavevector (K) for which the phase factor is unity,
and thus transformations(ie. quantum jumps Δ) between these intervals leaves the phase state unchanged.

Likewise, due to the duality of (R'·K), one can think of it as a particle at a particular (R').
There exists a series (Δn) of certain changes in wavevector (ΔK) at this point (R') for which the phase factor is unity,
and thus transformations(ie. quantum jumps Δ) between these wavevectors leaves the phase state unchanged.

**Note that scalar invariant (n), and the unit normal wave direction (n̂), are different things in the following derivation**

Δ(R'·K) = Δ(ct',r')·(ω/c,k) = Δ(ct',r')·(1/cT,n̂/λ) = Δ(ct'/cT - r'·n̂/λ) = Δ(t'/T - r'·n̂/λ) = -Δn
If we examine the time Δt' = 0 {simultaneity} case, we get:
-Δ(r'·n̂/λ) = -Δn
r'/λ = n
r' = nλ
2πr' = nλ : Note that this is the condition that an integer number (n) of wavelengths (λ) fit the circumference of a circle with radius r'
(i.e. it is de Broglie's Standing Wave Hypotreatise, with the additional implied relativistic criterion that it is the case for simultaneity)
And
Δ(2πr' /λ) = Δn
A change in the state of (r' and λ) is an integer multiple Δn, ie. the quantum jump
see Bohr Model, Matter Wave,

Now, combine this with P = ћK = (E/c,p) = ћ(1/cT,n̂/λ)
p = ћn̂/λ
p = ћ/λ
λp = ћΔnλp = Δnћ: We can multiply both sides by the integer (Δn)
Δ(r'p) = ΔnћL = nћ: the condition for quantization of angular momentum
(i.e. the Bohr Condition for Quantization)

Similarly, we can examine the Δ r_K = 0 {stationarity, maybe locality - along a worldline} case:
Δ(t' E) = -Δnћ,
which is totally analagous to Δ(r' p) = Δnћ

Thus, [Δ(R'·K) = -Δn], is an SR Lorentz Invariant method of Quantization.

Now, instead use the 4-TotalWaveVector K_T
[Δ(R'·K_T) = Δ(R·(K - q/ћA + K_geo) = Δ(R·K_particle) - (q/ћ)Δ(R·A_EM) + (R·K_geo) = -Δn]

P_T = P + qA + P_geo
K_T = K + (q/ћ)A + K_geo
K_T·X = K·X + (q/ћ)A·X + K_geo·X
-Φ_T = -Φ + (q/ћ)A·X - Φ_geo
Φ_T = Φ - (q/ћ)A·X + Φ_geo
Φ_T = Φ_particle + Φ_pot + Φ_geo
The total phase is the standard phase plus the effects of the 4-VectorPotential and the effects of a quantum geometric phase.

S = -(P_T·R) and ∂[S] = -P_T.
A more refined method is apparently something like:
I = ∮K_T·dR' = 2π(n + μ/4 + b/2)
(1/ћ)∮P_T·dR' = 2π(n + μ/4 + b/2)
-(1/ћ)∮∂[S]·dR' = 2π(n + μ/4 + b/2)
(1/ћ)∮∂[S]·dR' = -2π(n + μ/4 + b/2)
(1/ћ)∮(∂_t[S]dt - ∇[S]·dr') = -2π(n + μ/4 + b/2)
where n is a positive integer, b is a Maslov index, μ is a turning point fo the trajectory r
see Old Quantum Theory (Bohr-Sommerfield Quantization), Geometric (Berry) Phase, Einstein–Brillouin–Keller (EBK) method, Hamilton–Jacobi equation, Quantum Chaos, Action-Angle Coordinates, Landau Quantization,

The Dirac Equation Derived

It can be shown that spin comes from the Poincaré Symmetry of SR, not from a QM axiom.
Writing a 4-SpinMomentum then leads naturally to the Dirac Equation.

First, we will do a little pure mathematics:
Let {(a² - b²) = (a+b)(a-b) = c²}

We can multiply by an arbitrary factor (xy) on both sides:
(a² - b²)(xy) = (a+b)(a-b)(xy) = c²(xy)

If we impose the following constraint:
(a+b)x = (cy)
(a-b)y = (cx)

Then the separated equations are still true when multiplied together:
(a+b)x(a-b)y = (cy)(cx) → (a+b)(a-b)(xy) = c²(xy)

Now add and subtract the separated equations:
(a+b)x + (a-b)y = (cy) + (cx)
(a+b)x - (a-b)y = (cy) - (cx)

Gather terms in {a,b,c}:
a(x+y) + b(x-y) = c(x+y)
a(x-y) + b(x+y) = -c(x-y)

Let X = (x+y) and Y = (y-x) = -(x-y), just a change in variable names
aX - bY = cX
-aY + bX = cY

Rearrange:
aX - bY = cX
bX - aY = cY

Putting into matrix form:

[a - b]	[X]	=	[c 0]	[X]
[b - a]	[Y]	=	[0 c]	[Y]

or
Putting into suggestive matrix form...

([1 0]	a +	[0 -1]	b	)[X]	= c	[1 0]	[X]
([0 -1]	a +	[1 0]	b	)[Y]	= c	[0 1]	[Y]

And again, to confirm that this matches the original equation:
aX - bY = cX
bX - aY = cY
or
(a-c)X = (b)Y
(b)X = (a+c)Y

Multiply across
(a-c)X(a+c)Y = (b)X(b)Y
(a-c)(a+c)XY = (b)(b)XY
(a² - c²)XY = (b²)XY
(a² - c²) = b²
(a² - b²) = c²

So, mathematically:
(a² - b²) = c² is the defining equation, which holds equivalently for:

{(a² - b²)(xy) = (c²)(xy)}
or

([1 0]	a +	[0 -1]	b	)[X]	= c	[1 0]	[X]
([0 -1]	a +	[1 0]	b	)[Y]	= c	[0 1]	[Y]

It is only the nature of x,y and X,Y that is different.

All of the relativistic wave equations can be derived from a common source, the relativistic mass-energy relation, inc. spin, in an EM field.
Note that this formalism fits well with the Pauli Matrices and the Stern-Gerlach experiment.

4-Momentum P = (E/c,p)
4-Momentum inc. Spin P_S = Σ·P = Σ^μ_νP^ν = η_αβΣ^μα P^β = Ps^μ
Σ^μ_ν is the 4D (1,1)-Pauli Spin-Matrix Tensor = Diag[σ⁰,σ]
Σ^μν is 4D (2,0)-Pauli Spin-Matrix Tensor = Diag[σ⁰,-σ]

P_S = Diag[σ⁰,- σ]·P = Diag[σ⁰,- σ]·(E/c,p) = (σ⁰E/c,σ·p)

P_S = (ps⁰,ps) = (σ⁰E/c,σ·p)
with σ⁰as an identity matrix of appropriate spin dimension and σ is the Pauli Spin Matrix Vector

4-Momentum inc. Spin in External Field
with:
H = E_T = Hamiltonian = Total Energy Of System
p_T = Total 3-momentum Of System

4-TotalMomentum P_T = P + qA
4-Momentum P = P_T - qA
4-MomentumIncSpin P_s = (p_s⁰,p_s) = (σ⁰E/c,σ·p) = ( σ⁰(E_T/c - qφ/c),σ·(p_T - qa) )
P_s·P_s = (p_s⁰)² - (p_s)² = [σ⁰(E/c)]² - [σ·(p)]² = [σ⁰(E_t/c - qφ/c)]² - [σ·(p_t - qa)]² = (m_oc)² = (E_o/c)²

The 4-TotalMomentum (inc. External Field Minimal-Coupling and Spin)
P_s = Σ·P = Σ·(P_T - qA) = [σ⁰(E_T/c - qφ/c),σ·(p_T - qa)]
with Σ = Σ^μνas the Pauli Spin Matrices, and taking the Einstein summation gives the σ⁰and σ

P_s·P_s = (Σ·P)² = [Σ·(P_T - qA)]² = [σ⁰(E_T/c - qφ/c)]² - [σ·(p_T - qa)]² = (m_oc)²
(Σ·P )² = (m_oc)²
(Σ·∂)² = -(m_oc/ћ)²
(Σ·∂ )² + (m_oc/ћ)² = 0
(Σ·(D-(i/h)qA))² + (m_oc/ћ)² = 0

Now, to prove that this "Relativistic Pauli" Energy-Momentum equation can lead to the Dirac equation
Ps·Ps = [σ⁰(E_T/c - qφ/c)]² - [σ·(p_T -qa)]² = (ps⁰)² - (ps)² = (m_oc)² = (E_o/c)²
Ps·Ps = I(E_T/c - qφ/c)]² - [σ·(p_T -qa)]² = (ps⁰)² - (ps)² = (m_oc)² = (E_o/c)²
Ps·Ps = (ps⁰)² - (ps)² = (ps⁰ + ps) (ps⁰ - ps) = (m_oc)²
{(ps⁰)² - (ps)²}(xy) = (m_oc)²(xy)

From our math proof above, this is equivalent to:

([1 0]	ps⁰ +	[0 -1]	ps	)[X]	= (m_oc)I₂	[X]
([0 -1]	ps⁰ +	[1 0]	ps	)[Y]	= (m_oc)I₂	[Y]

([1 0]	σ⁰p⁰ +	[0 -1]	σ·p	)[X]	= (m_oc)I₂	[X]
([0 -1]	σ⁰p⁰ +	[1 0]	σ·p	)[Y]	= (m_oc)I₂	[Y]

Putting into highly suggestive matrix form...

([σ⁰ 0]	p⁰ +	[0 -σ]	·p	)[X]	= (m_oc)I₂	[X]
([0 -σ⁰]	p⁰ +	[σ 0]	·p	)[Y]	= (m_oc)I₂	[Y]

let Spinor Ψ =	[X]	and note that σ⁰ = I₂
	[Y]

this is equivalent to Dirac Gamma Matrices (in Dirac Basis)...

([I₂ 0]	p⁰ +	[0 -σ]	·p	)	Ψ= (m_oc)IΨ
([0 -I₂]		[σ 0]		)

(γ⁰p⁰ - γ·p)Ψ = (m_oc)IΨ
(Γ·P)Ψ = (m_oc)IΨ
(Γ·P) = (m_oc)
(Γ^μP_μ)Ψ = (m_oc)Ψ
iћ(Γ^μ∂_μ)Ψ = (m_oc)Ψ
The Dirac Relativistic Quantum Equation for spin 1/2 particles

also, using the same treatment...
Relativistic version (Relativistic Pauli Equation)
Ps·Ps = [σ⁰ (E_T/c - qφ/c)]² - [σ·(p_T -qa)]² = (m_oc)² = (E_o/c)²
[σ⁰ (E_T/c - qφ/c)]² - [σ·(p_T -qa)]² = (m_oc)²
[I(E_T/c - qφ/c)]² - [σ·(p_T -qa)]² = (m_oc)²
[I(E_T/c - qφ/c)]² - [I·(p_T -qa)]² - i[σ·((p_T x -qa) + (-qa x p_T))] = (m_oc)²
[I(E_T/c - qφ/c)]² - [I·(p_T -qa)]² - i[σ·iћq((-∇_T x -a) + ( -a x -∇_T))] = (m_oc)²
[I(E_T/c - qφ/c)]² - [I·(p_T -qa)]² - i[σ·iћq(B)] = (m_oc)²
[I(E_T/c - qφ/c)]² - [I·(p_T -qa)]² + ћq[σ·B] = (m_oc)²
[I(E_T/c - qφ/c)]² = [I·(p_T -qa)]² - ћq[σ·B] + (m_oc)²

or, for non-relativistic version (Standard Pauli Equation)
[I(E_T/c - qφ/c)]² - [σ·(p_T -qa)]² = (m_oc)²
[I(E_T/c - qφ/c)]² = [σ·(p_T -qa)]² + (m_oc)²
[I(E_T/c - qφ/c)] = (±) Sqrt [[σ·(p_T -qa)]² + (m_oc)²]
[I(E_T/c - qφ/c)] = (±) Sqrt [[σ·(p_T -qa)]² + (m_oc)²]
[I(E_T/c - qφ/c)] ~ (±) [[σ·(p_T -qa)]²/(2m_oc) + (m_oc)]
[I(E_T/c - qφ/c)] ~ (±) [([(p_T -qa)]² - ћq[σ·B])/(2m_oc) + (m_oc)]
[I(E_T - qφ)] ~ (±) [([(p_T -qa)]² - ћq[σ·B])/(2m_o) + (m_oc²)]
E_T ~ qφ (±) [([(p_T -qa)]² - ћq[σ·B])/(2m_o) + (m_oc²)]
where the - (ћq[σ·B])/(2m_o) is the Stern-Gerlach term

Photon Polarization

Derivation of the SR reason that the QM photon polarization only has 2 independent states, instead of 3 or 4.

4-Polarization Ε = (ε⁰,ε) → (ε·β,ε)
4-WaveVector K = (ω/c,k) = (ω/c,n̂ω/v_phase) = (ω/c)(1,β) = (1/cT,n̂/λ)
4-Polarization E = (ε⁰,ε): Normally as a typical 4-Vector it would have 4 independent components
However, we know empirically that the 4-Polarization E is orthogonal to the direction of propagation 4-WaveVector K
Ε·K = 0 = (ε⁰,ε)·(ω/c)(1,β) = (ω/c)(ε⁰ - ε·β) = 0: This is a Lorentz Invariant restriction
So, ε⁰ = ε·β
We can go ahead and simplify the 4-Polarization a bit with this new info
4-Polarization E = (ε·β,ε): Now it only has 3 independent components (ε)

However, we also know that the 4-Polarization is normalized to unity along a spatial direction.
This one is a bit trickier because we know that the 4-Polarization can have complex components (those representing circular polarization).
See the Jones Vector, Stokes Vector, Mueller Calculus, etc.
But, this can be accommodated using using standard complex notation...
Ε·E* = -1, Normalization to Spatial Unity, which is also a Lorentz Invariant Restriction

Ε·E* = -1 imposes
(ε·β)(ε*·β) -ε·ε* = -1
(ε·β)² -1 = -1
(ε·β)² = 0
ε·β = 0, so that the spatial components must be orthogonal, which is an additional constraining formula.

For a massive particle, there is always a rest frame with β = 0, so ε can have 3 independent components.
For a photonic particle, there is no rest frame. |β| = 1 always. ( ε·β = ε·n̂ = 0 ) is therefore an additional constraint,
limiting ε to 2 independent components, with polarization ε orthogonal to direction of photon motion n̂.

So, ( Ε·K = 0 ) and ( Ε·E* = -1 ) are both Lorentz Invariant Relations, which apply to all observers.

This appears to be related to the Ward-Takahashi Identity and Gauge-Fixing.

∂·U = 0 :Advection Equation (with γ as the advected quantity)

∂·J = 0 :Continuity Equation ∂·∂ = (-im_oc/ћ)² = -(m_oc/ћ)² :Wave Equation
Low Energy limiting-case Schrödinger: Diffusion Equation

CPT & SR Phase Connection, and eventually the Spin-Statistics Theorem

The Phase (Φ) is a Lorentz Scalar Invariant; All observers must agree on its value.

K·X = (ω/c,k)·(ct,x) = (ωt - k·x) = -Φ: Phase of SR Wave

We take the point of view of an observer operating on a particle at 4-Position X, which has an initial 4-WaveVector K.
The 4-Position X of the particle, the operation's event, will not change: we are applying the various operations only to the particle's 4-Momentum K.

Note that for matter particles:
K = (ω_o/c)T, with T as the Unit-Temporal 4-Vector T = γ(1,β), which defines the particle's worldline at each point.
The gamma factor ( γ ) will be unaffected in the following operations since it uses the absolute square of β: {β·β = |β|² = β*β = (β*β)* = ββ* = |-β|² , etc.}
γ = 1/√(1-β²).

For photonic particles, K = (ω/c)N, with N as the "Unit"-Null 4-Vector N = (1,n̂) and n̂ as a unit-spatial 3-vector.
All operations listed below work similarly on the 4-Null 4-Vector.
=====

Do a Time Reversal Operation: T
The particle's temporal direction is reversed & complex-conjugated:
T_T = - T* = γ(-1,β)*

Do a Parity Operation (Space Reflection): P
Only the spatial directions are reversed:
T_P = γ(1,-β)

Do a Charge Conjugation Operation: C
Feynman showed this is the equivalent of world-line reversal & complex-conjugation
This is the Feynman–Stueckelberg Interpretation, (Crossing), it changes all internal quantum #'s - charge, lepton #, etc.:
T_C = γ(-1,-β)*

=====
Pairwise combinations:
T_TP = T_PT = T_C = γ(-1,-β)*
T_TC = T_CT = T_P = γ(1,-β)
T_PC = T_CP = T_T = γ(-1,β)*,

which shows that a CP event is mathematically the same as a T event

T_CPT = T = γ(1,β)
T_CC = T = γ(1,β)
T_PP = T = γ(1,β)
T_TT = T = γ(1,β)

It is only the combination of all three ops, in any order: {C,P,T}, or repeats of the same op {C,C or P,P or T,T},
that leave the Unit-Temporal 4-Vector T, and thus the Phase K·X = Φ, Invariant.

*Note*, this is how I understand the CPT Theorem, I'm pretty sure it is not the standard interpretation.

According to the Wiki entry on the CPT Theorem : the CPT Theorem appeared for the first time, implicitly, in the work of Julian Schwinger in 1951 to prove the connection between spin and statistics. It continues saying: Since a sequence of two CPT reflections is equivalent to a 360-degree rotation, fermions change by a sign under two CPT reflections, while bosons do not. This fact can be used to prove the spin-statistics theorem.

See also: Wightman Axioms,

The Spin Statistics Theorem amounts to:

{ 1 = ±(-1)^2j}

where j is the spin of the particle and the ± gives the statistics choice: (+) bosonic/symmetric, (-)fermionic/antisymmetric.
If { j = 0,1,2,... = integer }, then (+) is chosen.
If { j = 1/2, 3/2,... = half integer }, then (-) is chosen.

I believe that this is ultimately going to be noticing that within the Poincaré Group, the continuous symmetry of the Rotation Operation occasionally overlaps and matches the discrete symmetry of the Exchange or Parity Operation.

See also: The Parity of Spherical Harmonics, Spin Spherical Harmonics, etc.
The spherical harmonics have well defined parity in the sense that they are either even or odd with respect to reflection about the origin. Reflection about the origin is represented by the operatorPΨ(r) = Ψ(- r). For the spherical angles, {θ,φ} this corresponds to the replacement {π - θ,π + φ}. The associated Legendre polynomials gives (−1)^{ℓ + m}and from the exponential function we have (−1)^m, giving together for the spherical harmonics a parity of (−1)^ℓ:
Y_ℓ^m(θ,φ) --> Y_ℓ^m(π - θ,π + φ) = (−1)^ℓY_ℓ^m(θ,φ)
This remains true for spherical harmonics in higher dimensions: applying a point reflection to a spherical harmonic of degree ℓ changes the sign by a factor of (−1)^ℓ.
Spin Spherical Harmonics Y_l,s,j,mare spinor eigenstates of the total angular momentum operator:
J²Y_l,s,j,m = j(j + 1)Y_l,s,j,m
J_zY_l,s,j,m = mY_l,s,j,m
where { j = l + s }
They are the natural spinorial analog of Vector Spherical Harmonics.

SRQM Relativistic Lagrangian Hamiltonian Diagram

Lagrangian/Hamiltonian Formalisms:

see Relativistic Lagrangian Mechanics
Relativistic Beta Factor β = u/c = v/c
Relativistic Gamma Factor γ = 1/√[1-β²]
4-Velocity U = U^μ = (U⁰,Uⁱ) = γ(c,u)
4-Momentum P = P^μ = (E/c,p) = (mc,p)
4-VectorPotential A = A^μ = (φ/c,a) = A[X] = A[(ct,x)] = (φ[(ct,x)]/c,a[(ct,x)]), often used for/as A_EM
4-PotentialMomentum Q = Q^μ = (U/c,q) = q(φ/c,a)
4-TotalMomentum P_T_particle = P_Tparticle^μ = (E_T/c,p_T) = (H/c,p_T) = (E/c + U/c,p + q) = (E/c + qφ/c,p + qa), meaning the sum of particle momentum and charged interaction potential momentum
4-TotalMomentum P_T_sys = P_Tsys^μ = (E_T/c,p_T) = (H/c,p_T) = Σ_n[P_T_particle(n)], meaning that the total 4-Momentum of a system is the sum of all individual particle 4-Momenta in the system

The whole Lagrangian/Hamiltonian connection is given by the relativistic identity:
γ = 1/√[1 - β²]
γ² = 1/(1 - β²)
(1 - β²)γ² = 1
(γ² - γ²β²) = 1
(γ² - 1) = γ²β²
( γ - 1/γ ) = (γβ²)
Now multiply by your favorite Lorentz Scalars... In this case for a free relativistic particle...
( γ - 1/γ )(P·U) = ( γβ²)(P·U)
( γ - 1/γ )(m_oc²) = ( γβ²)(m_oc²)
( γm_oc² - m_oc²/γ ) = γm_oc²β²
( γm_oc² - m_oc²/γ ) = γm_ou²
( γm_oc²) + (- m_oc²/γ ) = γm_ou·u
( γm_oc²) + (- m_oc²/γ ) = (p·u)
( H ) + ( L ) = (p·u)
The Hamiltonian/Lagrangian connection falls right out.
Note that neither (H) nor (L) are scalar invariants, due to the extra (γ) factors.

Now, including the effects of a potential:
4-VectorPotential A = (φ/c,a) { = (φ_EM/c,a_EM) for EM potential }
4-PotentialMomentum Q = qA due to 4-VectorPotential acting on charge (q)
4-TotalMomentum of System P_T = P + Q = P + qA = m_oU + qA = (H/c,p_T) = (γm_oc + qφ/c,γm_ou + qa)
A·U = γ(φ - a·u) = φ_o
P·U = γ(E - p·u) = E_oP_T·U = E_o + qφ_o = m_oc² + qφ_o
I assume the following as a valid SR relation:
A = (φ_o/c²)U = (φ/c,a) = (φ_o/c²)γ(c,u) = ((γφ_o/c), (γφ_o/c²)u) giving {φ = γφ_o and a = (γφ_o/c²)u}
P = (E_o/c²)U = (E/c,p) = (E_o/c²)γ(c,u) = ((γE_o/c), (γE_o/c²)u) giving {E = γE_o and p = (γE_o/c²)u = (γm_o)u} is analogous.

( γ - 1/γ ) = (γβ²)
( γ - 1/γ )(P_T·U) = ( γβ²)(P_T·U)
γ(P_T·U) + -(P_T·U)/γ = ( γβ²)(P_T·U)
γ(P_T·U) + -(P_T·U)/γ = (p_T·u)
( H ) + ( L ) = ( p_T·u )

Relativistic Hamiltonian H = γ(P_T·U)	Relativistic Lagrangain L = -(P_T·U)/γ	p_T·u = ( γβ²)(P_T·U) = H + L = γ(P_T·U) + -(P_T·U)/γ
H = γ(P_T·U) H = γ((P + Q)·U) H = γ(P·U + Q·U) H = γP·U + γQ·U H = γm_oU·U + γqA·U H = γm_oc² + qγφ_o H = γm_oc² + qφ H = ( γβ² + 1/γ )m_oc² + qφ H = ( γm_oβ²c² + m_oc²/γ) + qφ H = ( γm_ou² + m_oc²/γ) + qφ H = p·u + m_oc²/γ + qφ H = E + qφ H = ±c√[m_o²c² + p²] + qφ H = ±c√[m_o²c² + (p_T -qa)²] + qφ H = ±m_oc²√[1 + (p_T -qa)²/(m_o²c²)] + qφ	L = -(P_T·U)/γ L = -((P + Q)·U)/γ L = -(P·U + Q·U)/γ L = - P·U/γ - Q·U/γ L = -m_oU·U/γ - qA·U/γ L = -m_oc²/γ - qA·U/γ L = -m_oc²/γ - q(φ/c,a)·γ(c,u)/γ L = -m_oc²/γ - q(φ/c,a)·(c,u) L = -m_oc²/γ - q(φ - a·u) L = -m_oc²/γ - qφ + qa·u L = -m_oc²/γ - qφ_o/γ L = -(m_oc² + qφ_o)/γ	H + L = γ(P_T·U) - (P_T·U)/γ H + L = (γ - 1/γ)(P_T·U) H + L = ( γβ²)(P_T·U) H + L = ( γβ²)((P + Q)·U) H + L = ( γβ²)(P·U + Q·U) H + L = ( γβ²)(m_oc² + qφ_o) H + L = (γm_oβ²c² + qγφ_oβ²) H + L = (γm_ou·uc²/c² + qφ_oγu·u/c²) H + L = (γm_ou·u + qa·u) H + L = (p·u + qa·u) H + L = p_T·u
Rest Hamiltonian H_o = (P_T·U) = H/γ	Rest Lagrangian L_o = -(P_T·U) = γL	H_o + L_o = 0

General binomial approximation (1 + x)ⁿ ~ 1 + nx + O[x²] for |x| << 1
Let x = -(v/c)² and n = (1/2), then
(1 + x)ⁿ ~ 1 + nx
(1 + -(v/c)² )^(1/2) ~ 1 + (1/2)(-(v/c)²) = 1 - (v/c)²/2

Let x = -(v/c)² and n = (-1/2), then
(1 + x)ⁿ ~ 1 + nx
(1 + -(v/c)² )^(-1/2) ~ 1 + (-1/2)(-(v/c)²) = 1 + (v/c)²/2

The non-relativistic Hamiltonian H_non-rel is an approximation of the relativistic Hamiltonian H:
H = γ(m_oc² + qφ_o)
H = (1/√[1-(v/c)²])(m_oc² + qΦ_o)
now remove √ by assuming {|v| << c}, which gives (1/√[1-(v/c)²]) ~ [1 + (v/c)²/2 + O[(v/c)⁴] ]
H ~ [1 + (v/c)²/2])(m_oc² + qφ_oEM) = (m_oc² + qφ_o) + (1/2)(m_oc²v²/c² + qφ_ov²/c²) ~ (m_oc² + qφ_o) + (1/2)(m_ov² + ~0)
H ~ (1/2)(m_ov²) + (m_oc² + qφ_o)
H ~ (Kinetic) + (Rest + Potential) = T + V {for |v| << c}
H_non-rel = T + V

The non-relativistic Lagrangian L_non-rel is an approximation of the relativistic Lagrangian L:
L = -(m_oc² + qφ_o)/γ
-L = (m_oc² + qφ_o)/γ = √[1-(v/c)²](m_oc² + qφ_o)
now remove √ by assuming {|v| << c}, which gives √[1-(v/c)²] ~ [1 - (v/c)²/2 + O[(v/c)⁴] ]
-L ~ (m_oc² + qφ_o) - (1/2)(m_oc²v²/c² + qφ_ov²/c²) ~ (m_oc² + qφ_o) - (1/2)(m_ov² + ~0 )
L ~ (1/2)(m_ov²) - (m_oc² + qφ_o)
L ~ (Kinetic) - (Rest + Potential) = T - V {for |v| << c}
L_non-rel = T - V

Thus, (H ~ T + V = H_non-rel ) and (L ~ T - V = L_non-rel ) only in the non-relativistic limit (|v| << c)
H + L ~ (T + V) + (T - V) = 2T = 2 (1/2 m_ou·u) = p·u
Thus, ( H ) + ( L ) = (p·u) is always true, in both the relativistic and non-relativistic case.

H = ± m_oc²√[1 + (p_T -qa)²/(m_o²c²)] + qφ
H ~ ± m_oc²[1 + (p_T -qa)²/(2m_o²c²)] + qφ for |(p_T -qa)²/(m_oc)²| << 1
H ~ ± [m_oc² + (p_T -qa)²/(2m_o)] + qφ for |(p_T -qa)²/(m_oc)²| << 1 {non-relativistic limit}

SRQM Relativistic Euler-Lagrange Equation

SRQM Relativistic EM Equations of Motion

Lagrangian Eqns. of Motion, Covariant Formulation for EM:
===========================================
d/dτ[∂L_o/∂U] = ∂L_o/∂X : Generalized Relativistic Lagrange Eqn. (All parts are Lorentz Invariant)

∂L_o/∂X = d/dτ[∂L_o/∂U]
{∂/∂X - d/dτ[∂/∂U]}L_o = 0
{∂_X - d/dτ[∂_U]}L_o = 0
To always be true, part inside brackets must be zero
∂_X = d/dτ[∂_U] Units:[1/m] = [1/s]*[s/m]
Note similarity to:
U = d/dτ[X] Units:[m/s] = [1/s]*[m]
The Euler-Lagrange equations are just the differential form of the 4-Velocity : 4-Position relation

Standard Lagrangian (L) is NOT Lorentz Invariant, just like the energy E is not Lorentz Invariant.
L = -P_T·U/γ = -(P+qA)·U/γ

Get the Rest Lagrangian Lorentz Scalar in exactly the same way we get the Rest Energy, E = γE_o
Set the Lorentz Gamma Factor to 1, which is what happens when u = 0

L_o = -P_T·U = -(P+qA)·U

∂L_o/∂U = -P_T

d/dτ[∂L_o/∂U] = d/dτ[-P_T] = -d/dτ[P_T] = -d/dτ[P+qA] = -(F+d/dτ[qA]) = -(F+qd/dτ[A]) = -(F+qU·∂[A]) = -(F+qU_ν∂^ν[A])

∂L_o/∂X = ∂[-P_T]/∂X = -∂[P_T]/∂X = -∂[(P+qA)·U]/∂X = (0) + -q∂[A·U]/∂X = -q∂[U·A]/∂X = -q∂[U_νA^ν]/∂X = -qU_ν∂[A^ν]/∂X = -qU_ν∂[A^ν]
assuming the 4-Gradient of U is zero.

d/dτ[∂L_o/∂U] = ∂L_o/∂X
So,
-(F+qU_ν∂^ν[A]) = -qU_ν∂[A^ν]
(F+qU_ν∂^ν[A]) = qU_ν∂[A^ν]
F = qU_ν∂[A^ν] - qU_ν∂^ν[A]
F = qU_ν(∂[A^ν] - ∂^ν[A])
F^μ = qU_ν(∂^μ[A^ν] - ∂^ν[A^μ])
F^μ = qU_ν(∂^μA^ν - ∂^νA^μ)
F^μ = qU_ν(F^μ^ν)
F^μ = qU_νF^μ^ν
dP/dτ = qU_μF^μν

Can also put in form of a Lagrangian Density:
∂L_o/∂X - d/dτ[∂L_o/∂U] = 0: Alternate form
multiply by inverse of L_o
∂/∂X - d/dτ[∂/∂U] = 0
multiply by Lagrangian Density
∂L/∂X - d/dτ[∂L/∂U] = 0

Lagrangian Densities:
================
Lagrangian for a charged particle minimally coupled to EM field: must have the factor of (1/2) for the mass part since it has goes by square of U
L_{chargedparticle} = (1/2)m_oU·U + qA·U
I'm not sure that I buy this one though.
Since the rest Lagrangian L_o = -P_T·U = -(P+qA)·U
The non-EM part of L_o is -(P)·U = -m_oU·U, not (1/2)m_oU·U
Several books will mention that the Covariant Relativistic Lagrangian approach will only work for a single particle minimally coupled to an EM field.
They say that it doesn't work for other potentials.
However, my answer to this is: just how do you get the other potentials?
For the vast majority of experimental setups, you are dealing with particles in EM fields.
There are no physically-real Infinite Square wells or Harmonic osciallators.
There are particles interacting with each other gravitationally and via EM.

Standard EM Lagrangian Density (spin = 0, q ≠ 0): {for an EM potential}
L_EM = J_νA^ν - (1/4μ_o)F_αβF^αβ

Klein-Gordon Lagrangian Density (spin = 0, q = 0): {for a spin =0 particle}
L_KG = -(ћ²/m_o)∂_νψ*∂^νψ - (m_oc²)ψ*ψ

Dirac Lagrangian Density (spin = 1/2, q ≠ 0): {for an electron}
L_Dirac = (iћc)ψ̅γ_ν∂^νψ - (m_oc²)ψ̅ψ, with ψ̅ = ψ^†γ⁰

QED Lagrangian Density (spin = 1/2, q ≠ 0): {for an electron in an EM potential}
L_QED = (iћc)ψ̅γ_νD^νψ - (m _oc²)ψ̅ψ - (1/4μ_o)F_αβF^αβ, with ψ̅ = ψ^†γ⁰ and D^ν = ∂^ν - ieA^ν

QCD Lagrangian Density (spin = 1/2, q ≠ 0): {for a quark in a color potential}
L_QCD = Σ_n(iћc)ψ̅_nγ_νD^νψ_n - (m_onc²)ψ̅_nψ_n - (1/4)G^ν_αβG_ν^αβ

More on the Group Properties of Minkowski Space → Poincaré Group
from "Representations of the Symmetry Group of SpaceTime" by Kyle Drake, Michael Feinberg, David Guild, Emma Turetsky

Minkowski SpaceTime is the mathematical model of flat (gravity-less) space and time.
The transformations on this space are the Lorentz transformations, known as O(1,3).
The identity component of O(1,3) is SO⁺(1,3).
The component SO⁺(1,3) taken with the translations R^1,3 is the Poincaré group, which is the symmetry group of Minkowski SpaceTime.
However, physical experiments show that a connected double cover of the Poincaré is more appropriate in creating the symmetry group for actual SpaceTime.
Why the double cover of the Poincaré group?
What is so special about this group in particular that it describes the particles?
The answer lies in the way the group is defined.
Simply, it is the set of all transformations that preserve the Minkowski metric of Minkowski SpaceTime.
In other words, it is the set of all transformations of SpaceTime that preserve the speed of light.
SL(2,C) is the connected double cover of the identity component of SO⁺(1,3).
This is the symmetry group of SpaceTime: the double cover of the Poincaré group, SL(2,C) x R^1,3.

In 1939, Eugene Wigner classified the fundamental particles using the irreducible representations of the double cover of the Poincaré group.
Wigner was motivated by the idea that symmetry underlies all physical laws.
In particular, a physical experiment should come up with the same results regardless of where, when, or what orientation the experiment is done in.
An experiment's results should also be invariant whether the experiment is at rest or moving at a constant velocity.
It turns out the symmetries of physics go further than this.
It is common to combine several systems together such as when protons and electrons combine to form atoms.
When this is done, the overall symmetry of the system should be related to the individual symmetries of its components.
These components are the irreducible representations [3].
The double cover of the Poincaré group acts to classify the fundamental particles in physics and explain patterns in their behaviors.
In particular, the particles are most easily classified by the irreducible representations of the double cover of the Poincaré group.
The representations are determined by the different orbits in the group.
These orbits serve to classify types of particles.
The first two types of orbits correspond to the value m² > 0.
The value m² is equivalent to the idea of mass in physics.
Thus elements in the first two orbits correspond to massive particles which travel slower than the speed of light.
The particles that correspond to the light cones are those with m² = 0, which are particles that travel at the speed of light.
Examples of these particles are photons, from the which the light cone gains its name, and gravitons, which currently only exist in theory.
The particles on the single-sheet hyperboloid with values m² < 0 are called tachyons.
They travel faster than the speed of light and have imaginary mass.
As tachyons have never been observed, we will not find the representations corresponding this orbit.
Finally, the orbit in which m² = 0 and the particles are not moving through time corresponds to vacuum.
Vacuum is devoid of all particles, and thus is uninteresting to the purposes of this paper.
It is somewhat surprising that the correspondences between the orbits of the double cover of the Poincaré group and types of particles line up as well as they do.
The spin values of particles predicted by physicists are exactly the values that come as a result of finding the irreducible representations of the double cover of the Poincaré group.
This fact is further explained by the fact that the Poincaré group's covering space is connected and has nice properties that emulate those observed in quantum spin.

Identical Particles:

All possible individual states of 2 Distinguishable Particles with 2 States each:
| ↑ ⟩| ↑ ⟩
| ↑ ⟩| ↓ ⟩
| ↓ ⟩| ↑ ⟩
| ↓ ⟩| ↓ ⟩

Exchange operator E:
E| ↑ ⟩| ↑ ⟩ = k| ↑ ⟩| ↑ ⟩
E| ↑ ⟩| ↓ ⟩ = k| ↓ ⟩| ↑ ⟩
E| ↓ ⟩| ↑ ⟩ = k| ↑ ⟩| ↓ ⟩
E| ↓ ⟩| ↓ ⟩ = k| ↓ ⟩| ↓ ⟩

E²| Ψ ⟩ = k²I| Ψ ⟩, because the first exchange swaps the particles, the 2nd exchange swaps them back to original state

Thus, eigenvalues of E are k = ±1, with ( + 1) = Symmetric, (-1) = AntiSymmetric
E| Ψ_s⟩ = + 1| Ψ_s⟩
E| Ψ_a⟩ = -1| Ψ_a⟩

General State Vector of 2 particles (w 2 states ea):
| Ψ ⟩ = a| ↑ ⟩| ↑ ⟩ + b| ↑ ⟩| ↓ ⟩ + c| ↓ ⟩| ↑ ⟩ + d| ↓ ⟩| ↓ ⟩
E| Ψ ⟩ = ±( a| ↑ ⟩| ↑ ⟩ + c| ↑ ⟩| ↓ ⟩ + b| ↓ ⟩| ↑ ⟩ + d| ↓ ⟩| ↓ ⟩ )

If Symmetric and Indistinguishable, then a = a, b = c, c = b, d = d, giving a Boson Triplet state:
| Ψ_s⟩ = a| ↑ ⟩| ↑ ⟩ + b (| ↑ ⟩| ↓ ⟩ + | ↓ ⟩| ↑ ⟩ ) + d| ↓ ⟩| ↓ ⟩

If AntiSymmetric and Indistinguishable, then a = -a = 0, b = -c, c = -b, d = -d = 0, giving a Fermion Singlet state:
| Ψ_a⟩ = b (| ↑ ⟩| ↓ ⟩ - | ↓ ⟩| ↑ ⟩ )

All possible individual states of 2 Distinguishable Particles (x1,x2) with 2 states ( + ,-):

Probability	\| ↑ ⟩ State	\| ↓ ⟩ State	Ket Tensor Product Representaion
1/4	1, 2		\| ↑ ⟩\| ↑ ⟩
1/4	1	2	\| ↑ ⟩\| ↓ ⟩
1/4	2	1	\| ↓ ⟩\| ↑ ⟩
1/4		1, 2	\| ↓ ⟩\| ↓ ⟩

All possible individual states of 2 Symmetric Indistinguishable Particles (x,x) with 2 states ( + ,-):

Probability	\| ↑ ⟩ State	\| ↓ ⟩ State	Ket Tensor Product Representation
1/3	x,x		\| ↑ ⟩\| ↑ ⟩ = \| 1,1 ⟩
1/3	x	x	1/√[2]*( \| ↑ ⟩\| ↓ ⟩ + \| ↓ ⟩\| ↑ ⟩ ) = \| 1,0 ⟩
1/3		x,x	\| ↓ ⟩\| ↓ ⟩ = \| 1,-1 ⟩

All possible individual states of 2 AntiSymmetric Indistinguishable particles (x,x) with 2 states ( + ,-):

Probability	\| ↑ ⟩ State	\| ↓ ⟩ State	Ket Tensor Product Representaion
1	x	x	1/√[2]*(\| ↑ ⟩\| ↓ ⟩ - \| ↓ ⟩\| ↑ ⟩ ) = \| 0,0 ⟩

Particle Statistics for 2 particles (2 states ea): **Note** b = boson annihilation, b^† = boson creation, f = fermion annihilation, f^† = fermion creation

Particles	Statistics	Energy Occupation	Principle	Canonical Commutation	Both (+)	Both (-)	One each ( + ,-)
Bosons	Bose-Einstein	<N_i> = g_i/(e^[(ε_i -μ)/kT] - 1)	Agglutination or Congregation	[b_α,b_β] = [b^†_α,b^†_β] = 0 [b_α,b^†_β] = b_αb^†_β - b^†_βb_α = δ_αβ	1/3	1/3	1/3
Distinguishable	Maxwell-Boltzmann	<N_i> = g_i/(e^[(ε_i -μ)/kT] + 0)	Simple Random		1/4	1/4	1/2
Fermions	Fermi-Dirac	<N_i> = g_i/(e^[(ε_i -μ)/kT] + 1)	Pauli Exclusion	{f_α,f_β} = {f^†_α,f^†_β} = 0 {f_α,f^†_β} = f_αf^†_β + f^†_βf_α = δ_αβ	0	0	1

*Note* in the limit of {|(ε_i -μ)/kT|>> 0 }, both Boson and Fermions approach Maxwell-Boltzmann statistics

Based on relativity, for equal time measurements one must have spacelike operators which either commute or anti-commute.
In other words, (anti)commutation relations of a causal field must disappear outside the lightcone, for spacelike separations.
This is the conditional of Local Commutativity, and imposes (anti)symmetric particle statistics on the states.

Define Field Operators (Annihilation and Creation Operators that act at certain SpaceTime points):

Particles	Field Operator	Annihilation,Annihilation	Creation,Creation	Annihilation,Creation
Bosons	Φ_b(r) = Σ_j[e^(k_j·r)b_j]	[Φ_b(r),Φ_b(r')] = 0 or [Φ_b(r),Φ_b(r')]_- = 0	[Φ^†_b(r),Φ^†_b(r')] = 0 or [Φ^†_b(r),Φ^†_b(r')]_- = 0	[Φ_b(r),Φ^†_b(r')] = ⟨ r\|r'⟩ = δ³(r-r') or [Φ_b(r),Φ^†_b(r')]_- = ⟨ r\|r'⟩ = δ³(r-r')
Fermions	Φ_f(r) = Σ_j[e^(k_j·r)f_j]	{Φ_f(r),Φ_f(r')} = 0 or [Φ_f(r),Φ_f(r')]₊ = 0	{Φ^†_f(r),Φ^†_f(r')} = 0 or [Φ^†_f(r),Φ^†_f(r')]₊ = 0	{Φ_f(r),Φ^†_f(r')} = ⟨ r\|r'⟩ = δ³(r-r') or [Φ_f(r),Φ^†_f(r')]₊ = ⟨ r\|r'⟩ = δ³(r-r')

where:

The annihilation operator of either type acting on the vacuum| 0 ⟩ gives 0.
Φ_b(r)| 0 ⟩ = 0
Φ_f(r)| 0 ⟩ = 0

The creation operator of either type acting on the vacuum| 0 ⟩ gives a single particle state at point r.
Φ^†_b(r)| 0 ⟩ = | b(r) ⟩
Φ^†_f(r)| 0 ⟩ = | f(r) ⟩

Φ^†_f(r)Φ^†_f(r)| 0 ⟩ = 0
because {Φ^†_f(r),Φ^†_f(r')} = 0 = Φ^†_f(r)Φ^†_f(r') + Φ^†_f(r)Φ^†_f(r')
letting r = r', we get Φ^†_f(r)Φ^†_f(r) + Φ^†_f(r)Φ^†_f(r) = 2Φ^†_f(r)Φ^†_f(r) = 0
Thus, two identical fermions cannot be placed in the same state at the same point r.

Bosons are not so restricted.
[Φ^†_b(r),Φ^†_b(r')] = 0 = Φ^†_b(r)Φ^†_b(r') - Φ^†_b(r)Φ^†_b(r')
letting r = r', we get Φ^†_b(r)Φ^†_b(r) - Φ^†_b(r),Φ^†_b(r) = 0
Thus the Φ^†_b(r)Φ^†_b(r) is not restricted at all.

Covariant Commutation Relations:

Taking the KG field as a typical example, we shall calculate [φ(x),φ(y)] for two arbitrary SpaceTime points.
φ = φ⁺ + φ^-

[φ⁺(x),φ⁺(y)] = [φ^-(x),φ^-(y)] = 0 since φ⁺ only contains absorption operators and φ^- only contains creation operators

[φ(x),φ(y)] = [φ⁺(x),φ^-(y)] + [φ^-(x),φ⁺(y)]

[φ⁺(x),φ^-(y)] = (ћc²)/(2V)Σ_kk' ( [a(k),a^†(k')] (e^(-ikx + ik'y))/(ω_kω_k')^(1/2) ) = (ћc²)/(2(2π)³)∫(d³k/ω_k) e^-ik(x-y)

∆⁺(x) = (-ic)/(2(2π)³)∫(d³k/ω_k) e^-ikx, where k₀ = ω_k/c

[φ⁺(x),φ^-(y)] = iћc∆⁺( x - y )

[φ^-(x),φ⁺(y)] = -iћc∆⁺( y - x ) = iћc∆^-( x - y )

[φ(x),φ(y)] = iћc∆( x - y )

∆(x) = ∆⁺(x) + ∆^-(x) = (-ic)/((2π)³)∫(d³k/ω_k) sin(kx)

∆(x) = (-i)/((2π)³)∫(d⁴k) δ(k² - μ²) ε(k₀) e^-ikx

ε(k₀) = (k₀)/|(k₀)| = {+1 if (k₀)>0, -1 if (k₀)< 0}

[φ(x,t),φ(y,t)] = iћc∆( x - y,0 ) = 0

Everyday Special Relativistic Effects

Since the speed of light is so large, it is difficult to come up with some ordinary type phenomena that rely on SR. There are a few, however.
Look up. :) See those really bright shiny things? All powered by fusion fire = Relativistic.

Relativistic quantum chemistry:
The yellowish color of the elements gold and cesium, which would otherwise be silvery/white: http://www.fourmilab.ch/documents/golden_glow/
The corrosion resistance of the element gold
Low melting point of element Mercury
About 10 of the 12 volts of a car's lead-acid battery due to relativistic effects, tin-acid batteries (similar outer orbitals) too weak
Viewpoint: Heaviest Element Has Unusual Shell Structure: significant impact of relativistic effects upon the shell structure (Jan 2018),

Navigation:
GPS Satellite system - Would go out of sync within minutes without the relativistic corrections, up to about 10 km difference /day
( Hafele-Keating Experiment ) - Time differences of atomic clocks carried on airliners.

EM:
Homopolar/Unipolar generator/motor - solution to Faraday's Paradox : http://www.physics.umd.edu/lecdem/outreach/QOTW/arch11/q218unipolar.pdf
Relativistic electron diffraction, or any other high speed electron experiments
Faraday's Law of Induction, where a moving magnet generates an electric field, for instance current along a wire
A plain old electromagnet, where the magnetic field is generated by moving electrons
The Moving Magnet and Conductor Problem

Various:
4 Ways You Can Observe Relativity In Everyday Life
8 Ways You Can See Einstein's Theory of Relativity in Real Life
10 Ways You See Einstein's Theory of Relativity in Real Life
Einstein's Relativity and Everyday Life - Physics Central

5 Recent Tests That Prove Einstein Right
GPS Satellite system
Electromagnetism, Relativistic Electromagnetism
Relativistic Quantum Chemisty (gold's yellow color, gold's non-corrosiveness, liquid mercury, etc.)
Nuclear Power (fission, fusion)
Rømer's Determination of the Speed of Light (using the moons of Jupiter)
Measure the Speed of Light using a Microwave Oven
Police Radar Speed Detection using Doppler Shift

Fizeau's Experiment of light in moving water
Cyclotron frequency of electron in magnetic field, increased effective mass from relativistic gamma factor
Muon travel time thru atmosphere
In atomic physics, the fine structure describes the splitting of the spectral lines of atoms due to 1st order relativistic corrections. Spin-orbit splitting.
Cherenkov Radiation : Matter particles moving thru a medium at greater than the local speed of light thru the medium emit Cerenkov radiation.
Relativity gives us fermions and Fermi-Dirac statistics and the whole structure of matter (i.e. Periodic Table of Elements) relies on the nature of fermions.
Relativity explains low energy aspects of the microscopic structure of matter, such as atomic spectra.
It is a general property for any interacting fermion to show spin-orbit behavior, a consequence of Lorentz Invariance.
Magnetism as the dynamic effect of moving electrical charges.
Cathode Ray Tubes, CRT's, in old style television sets and computer monitors, had electrons moving at up to 30% c, and the magnets controlling the beam had to be shaped with relativistic effects accounted for.
Nuclear power: One gets the massive power amounts from fission and fusion reactions based on the relativity, which gives magnitudes more power than regular chemical reactions.
Sunlight: It's based on nuclear fusion, which requires relativity.
Astronomy: Gravitational Lensing, Einstein Rings, etc.
Aberration of Light

Slow moving clocks:
The measurement of time dilation at everyday speeds has been accomplished as well. Chou et al. (2010) created two clocks each holding a single 27Al⁺ ion in a Paul trap. In one clock, the Al⁺ion was accompanied by a 9Be⁺ion as a "logic" ion, while in the other, it was accompanied by a 25Mg⁺ion. The two clocks were situated in separate laboratories and connected with a 75 m long, phase-stabilized optical fiber for exchange of clock signals. These optical atomic clocks emitted frequencies in the petahertz (1 PHz = 10¹⁵Hz) range and had frequency uncertainties in the 10^-17range. With these clocks, it was possible to measure a frequency shift due to time dilation of ~10^-16at speeds below 36 km/h (< 10 m/s, the speed of a fast runner) by comparing the rates of moving and resting aluminum ions.It was also possible to detect gravitational time dilation from a difference in elevation between the two clocks of 33 cm.

Some more Tensor Stuff

Tensor T^μν = A^μB^ν

time-time
T⁰⁰

time-space
T^0j

space-time
Tⁱ⁰

space-space
T^ij

11	12	13
21	22	23
31	32	33

Tensor T^μν

T⁰⁰	T⁰¹	T⁰²	T⁰³
T¹⁰	T¹¹	T¹²	T¹³
T²⁰	T²¹	T²²	T²³
T³⁰	T³¹	T³²	T³³

Has at most 16 independent components

Tensor T_μν = η_μρη_νσT^ρσ = η_μρη_νσA^ρB^σ

T₀₀	T₀₁	T₀₂	T₀₃
T₁₀	T₁₁	T₁₂	T₁₃
T₂₀	T₂₁	T₂₂	T₂₃
T₃₀	T₃₁	T₃₂	T₃₃

T⁰⁰	-T⁰¹	-T⁰²	-T⁰³
-T¹⁰	+T¹¹	+T¹²	+T¹³
-T²⁰	+T²¹	+T²²	+T²³
-T³⁰	+T³¹	+T³²	+T³³

The lowered-indicies form of a tensor just negativizes the (time-space) and (space-time) sections of the upper-indices tensor

Symmetric Tensor S^μν : ([S^μν] = [S^νμ])

S⁰⁰	S⁰¹	S⁰²	S⁰³
S¹⁰	S¹¹	S¹²	S¹³
S²⁰	S²¹	S²²	S²³
S³⁰	S³¹	S³²	S³³

S⁰⁰	S⁰¹	S⁰²	S⁰³
+S⁰¹	S¹¹	S¹²	S¹³
+S⁰²	+S¹²	S²²	S²³
+S⁰³	+S¹³	+S²³	S³³

Has at most 10 independent components: Can be created as S^μν = (T^μν + T^νμ)/2

Anti-Symmetric Tensor A^μν : ([A^μν] = -[A^νμ])

A⁰⁰	A⁰¹	A⁰²	A⁰³
A¹⁰	A¹¹	A¹²	A¹³
A²⁰	A²¹	A²²	A²³
A³⁰	A³¹	A³²	A³³

0	A⁰¹	A⁰²	A⁰³
-A⁰¹	0	A¹²	A¹³
-A⁰²	-A¹²	0	A²³
-A⁰³	-A¹³	-A²³	0

Has at most 6 independent components: Can be created as A^μν = (T^μν - T^νμ)/2

Then T^μν = (S^μν + A^νμ): Any rank-2 tensor can be composed of a symmetric part + an antisymmetric part.

Tensor Format of Various Theories

	(Vacuum) Field Equations	(Sourced) Field Equations Minkowski Metric Lorentz Gauge	Equations of Motion	Potential Φ	Independent Parameters
Newton CM	g^ijΦ_,ij = 0	g^ijΦ_,ij = ∇·∇Φ = 4πGρ_m	d²/dt²[Xⁱ] = -g^ijΦ_{, j} = -∂Φ/∂Xⁱ d²/dt²[x] = a = -∇Φ	Scalar = (0-Tensor)	1
Maxwell SR	g^μνΦ_ρ,μν = 0	g^μνΦ_ρ,μν = (∂·∂)Φ_ρ = μ_oJ_ρ (∂·∂)A = μ_oJ (∂·∂)(φ/c,a) = μ_o(ρ_ec,j) (∂·∂)φ = μ_oρ_ec² = ρ_e/ε_o ∇·∇φ = -ρ_e/ε_o {in time-independent potential)	(these assume constant restmass m_o) d²/dτ²[X^μ] = -(q/cm_o)g^μα(Φ_α,β - Φ_β,α)(dX^β/dτ) A^μ = -(q/cm_o)g^μα(Φ_α,β - Φ_β,α)U^β F^μ = qU_ν(∂^μA_EM^ν - ∂^νA_EM^μ) = qU_νF^μν	4-Vector = (1-Tensor)	4
Einstein GR	g^μνΦ_ρσ,μν + ... = 0		d²/dτ²[X^μ] = -(1/2)g^μα(g_αβ,γ + g_αγ,β - g_βγ,α) (dX^β/dτ)(dX^γ/dτ)	Tensor = (2-Tensor)	10

Inertial/Geodesic Motion (no Symmetry/Charge Forces) of Various Limiting Cases: GR→{"Flat" Minkowski SpaceTime}→SR→{Low Velocity}→CM

Approximation Level	Equation of Motion (Positions)	Equation of Motion (Velocities)	Limiting Case
Einstein GR (base/fundamental)	d²X^σ/dτ² + (Γ^σ_μν)(dX^μ/dτ)(dX^ν/dτ) = 0	dU^σ/dτ + (Γ^σ_μν)(U^μ)(U^ν) = 0	Geodesic Motion - no Symmetry/Charge Forces
Einstein SR	d²X^σ/dτ² = 0	dU^σ/dτ = d/dτ[U^σ] = 0 γdU^σ/dt = γd/dt[U^σ] = 0	Geodesic Motion - no Symmetry/Charge Forces "Flat" Minkowski SpaceTime (Γ^σ_μν) → 0
Newton CM	d²X^σ/dt² = 0	dU^σ/dt = 0	Geodesic Motion - no Symmetry/Charge Forces "Flat" Minkowski SpaceTime (Γ^σ_μν) → 0 Low Velocity (\|v\| << c; γ → 1, τ → t)

Einstein Field Equations:
G_μν + Λg_μν = (8πG/c⁴)T_μν
R_μν - (1/2)Rg_μν + Λg_μν = (8πG/c⁴)T_μν

where
R_μν is the Ricci Curvature Tensor, (represents the amount by which the volume of a small wedge of a geodesic ball in a curved Riemannian manifold deviates from standard ball in Euclidean space)
g_μν is the Metric Tensor, (represents all the geometric and causal structure of SpaceTime)
T_μν is the Stress-Energy Tensor, (represents the density and flux of energy and momentum in SpaceTime)

G_μν = R_μν - (1/2)Rg_μν
G_μν is the Einstein Tensor, (represents the curvature of a pseudo-Riemannian manifold, that part of the gravitational field due to immediate presence of energy-momentum)
aka Trace-reversed Ricci Tensor in 4D

R is the Scalar Curvature, (represents the amount by which the volume of a small geodesic ball in a Riemannian manifold deviates from that of the standard ball in Euclidean space)
Λ is the Cosmological Constant,
========================

Other Important Tensors:
H_μνσ is the Lanczos Tensor,
R_ρσμν is the Riemann Curvature Tensor,
Using Ricci Decomposition: R_ρσμν = S_ρσμν + E_ρσμν +C_ρσμν where S_ρσμν is scalar part, E_ρσμν is semi-traceless part, C_ρσμν is fully-traceless part Weyl Tensor,
C_ρσμν is the Weyl Tensor, (measures the deviation of a semi-Riemannian manifold from conformal flatness, that part of the gravitational field which can propagate as a gravitational wave through empty space)
T_ρσμν is the Bel-Robinson Tensor, (constructed from the Weyl Tensor in a manner analogous to the way the EM Stress-Energy Tensor is constructed from the Faraday EM Tensor)
J_μνσ is the Cotton Tensor,
B_μν is the Bach Tensor,
P_μν is the Schouten Tensor,
P^ρσ_μν is the Plebanski Tensor,
F_μν is the Faraday EM Tensor,
T_μν is the EM Stress-Energy Tensor, see also the Belinfante-Rosenfeld Stress-Energy Tensor,
G_μν is the Gluon Field Strength Tensor,
S_μνσ is the Spin Tensor,
M_μν is the Relativistic Angular Momentum Tensor,
T_μνσ is the Torsion Tensor,
K_μνσ is the Contorsion Tensor,
Φ_μν is the Tidal Tensor, aka the ElectroGravitic Tensor, see also the related MagnetoGravitic Tensor and TopoGravitic Tensor, via Bel Decomposition,
δ_μ^ν is the Kronecker Delta Tensor,
ε_ρσμν is the Levi-Civita Tensor,
see also Obstruction Tensor, Ricci Calculus, Curvature Invariants, Carminati-McLenaghan Invariants,

The Einstein GR field equations can be written as first order differential equations in the Weyl tensor C_abc^d (Jordan's formulation),
The Weyl tensor can be written as a first order differential equation in a three index tensor called the Lanczos tensor H_abc.

The Maxwell EM field equations can be written as first order differential equations in the Faraday tensor F^μν
The Faraday tensor can be written as a first order differential equation in the vector potential A^μ

Thus, the Lanczos tensor plays a similar role in general relativity to that of the vector potential in electromagnetic theory.
The Aharonov-Bohm effect shows that when quantum mechanics is applied to electromagnetic theory the vector potential is dynamically significant, even when the electromagnetic field tensor F^μν vanishes.
There is the possibility of a similar effect in GR...

Note: In the following chart all tensor indices range from 0..3, for both Latin and Greek

	Field Equations in Lorenz Gauge (Divergence of Basic Field = 0)	Full Field Equations	CurrentDensity	Higher Field Construction	Basic Field
SR EM 4-Vector Style	(∂·∂)A_EM = μ_oJ with (∂·A_EM) = 0	∂[F^ρσ] = (∂·∂)A_EM - ∂(∂·A_EM) = μ_oJ	4-CurrentDensity J		4-VectorPotential A_EM
SR EM Tensor Style	(∂_μ∂^μ)A_EM^ν = μ_oJ^ν with (∂_νA_EM^ν) = 0	∂_μF^μν = ∂_μ(∂^μA_EM^ν - ∂^νA_EM^μ) = μ_oJ^ν	4-CurrentDensity J^ν	SR Faraday Tensor F^μν = (∂^μA_EM^ν - ∂^νA_EM^μ)	4-VectorPotential A_EM^μ
SR EM (,) Style		F^μν_,μ = μ_oJ^ν
GR (;) Style	(∂·∂)H_abc = (∂_μ∂^μ)H_abc = J_abc -2R_c^dH_abd+R_a^dH_bcd+R_b^dH_acd +(H_dbeg_ac-H_daeg_bc)R^de+RH_abc/2	(Jordan Formulation) C_abc^d_;d = (some constant)J_abc	Cotton Tensor (~Matter Current) J_abc = R_ca;b-R_cb;a +(g_cbR_;a-g_caR_;b)/6	Weyl Tensor C_abcd = H_abc;d-H_abd;c+H_cda;b-H_cdb;a - (g_ac(H_bd+H_db)-g_ad(H_bc+H_cb)+g_bd(H_ac+H_ca)-g_bc(H_ad+H_da))/2 +2H^ef_e;f(g_acg_bd-g_adg_bc)/3 where H_bd=H_b^e_d;e-H_b^e_c;d	Lanczos TensorPotential H_abc

There are wave equations in both the 4-VectorPotential and the Lanczos TensorPotential.

Derived Equations and Newtonian Limts:

*Note*
When deriving the Newtonian Limit, always use the Low Velocity (v<<c) or Low Energy (E<<m_oc²) approximations, as these apply to "real" situations
Do not use the (c --> Infinity) approximation - while technically making the math work, it is however an unphysical situation

4-Vector(s)	Type	Relativistic Law	Newtonian Limit Low Velocity (v<<c) or Low Energy (E<<m_oc²) Basically, β → 0, γ → 1
R = (ct,r)	4-Position	(ct,r) is single 4-vector entity t and r related by Lorentz transform	t independent from r t is independent scalar, r is independent 3-vector
ΔR = (cΔt,Δr)	4-Displacement	Relative Simultaneity Δt' = γ(Δt - β·Δr/c)	Absolute Simultaneity Δt' = Δt
U = dR/dτ	4-Velocity	Relativistic Composition of Velocities u_rel = =[u₁+u₂]/(1+β₁·β₂) =[u₁+u₂]/(1+u₁·u₂/c²) Imposes Universal Speed Limit of c	Additive Velocities u₁₂ = u₁ + u₂ Unlimited Speed
A = dU/dτ	4-Acceleration	Relativistic Larmor Formula Power radiated by moving charge P = = -( q²/ 6πε_oc³)(A·A) = -(μ_oq²/6πc)(A·A) = (μ_oq²/6πc) γ⁶/ (a² - (\|u x a\|)²/c²)	Newtonian Larmor Formula Power radiated by a non-relativistic moving charge P = (μ_oq²/6πc)(a²)
P = m_oU	4-Momentum	Einstein Energy-Mass Relation E = γ m_oc² = Sqrt[ m_o²c⁴ + p·p c² ]	Total Energy = Rest Energy + Kinetic Energy E = m_oc² + (p²/2m_o)
∂·P	Divergence of 4-Momentum	Local? Conservation of 4-Momentum	Conservation of Energy, Conservation of Momentum
P₁·P₂	Particle Interaction	Conservation of 4-Momentum	Conservation of Energy, Conservation of Momentum, sometimes Conservation of Kinetic Energy
K = (ω/c,k) = (1/ћ)P = (m_o/ћ)U = (ω_o/c²)U	4-WaveVector and 4-Velocity	Relativistic Doppler Effect, inc. Transverse Doppler Effect a_{o_obs} = = a_{o_emit} / γ(1 - (n·v/c)) = a_{o_emit} / γ(1 - (n·β)) = a_{o_emit} √[1+\|β\|]√[1-\|β\|] / (1 - (n·β)) Relativistic Aberration Effect cos(ø_{_obs}) = [cos(ø_{_emit})-β]/[1-βcos(ø_{_emit})] Relativistic Wave Speed, all elementary particles, matter or photonic λf = c/β = v_phase	Regular Doppler Effect a_{o_obs} = a_{o_emit} √[1+\|β\|]√[1-\|β\|] Newtonian Aberration = None cos(ø_{_obs})= cos(ø_{_emit}) Newtonian Wave Speed, only photonic particles (a rare case when the lightspeed case is chosen for Newtonian description) λf = c
P and K	4-Momentum and 4-WaveVector	Compton Scattering (λ'-λ) = (h/m_oc)(1-cos[ø]) (m_oc²)(1/E'-1/E) = (1-cos[ø]) Ratio of photon energy after/before collision P[E,ø] = 1/[1+(E/m_oc²)(1-cos[ø])] see also Klein-Nishina formula	Thompson Scattering Ratio of photon energy after/before collision: E<<m_oc² P[E,ø] → 1
∂ = -iK	4-Gradient	D'Alembertian & Klein-Gordon Equation ∂_t²/c² = ∇·∇-(m_oc/ћ)²	Schrödinger Equation (i ћ)( ∂_t ) = - (ћ)²(∇)²/2m_o
∂·J	Divergence of 4-Current	Conservation of 4-EM_CurrentDensity ∂·J = ∂/c∂t(cp)+∇·j = ∂p/∂t +∇·j = 0	Conservation of 4-EM_CurrentDensity ∂·J = ∂/c∂t(cp)+∇·j = ∂p/∂t +∇·j = 0
J_prob	Probability CurrentDensity	Conservation of ProbabilityCurrentDensity ρ = (iћ/2m_oc²)(ψ* ∂_t[ψ]-∂_t[ψ] ψ) j = (-iћ/2m_o)(ψ ∇[ψ]-∇[ψ] ψ) ∂·J_prob* = ∂ρ/∂t +∇·j = 0 ρ = γ(ψ*ψ) for time separable wave functions Relativistically, this is conservation of the number of worldlines thru a given SpaceTime event	Conservation of Probability ∂·J_prob = ∂ρ/∂t +∇·j = 0 ρ = (ψ*ψ) for time separable wave functions Typically set so that the sum over all quantum states in space = 1 At low energies/velocities, this appears as the conservation of probability of a given wavefunction at a given SpaceTime event - In other words, the probability interpretation of a wavefunction is just a Newtonian approximation to the more correctly stated conservation of relativistic worldlines. This is why the problem of positive definite probabilities and probabilities >1 vanishes once you consider anti-particles and conservation of charged currents.
A_EM = (Φ_EM/c, a_EM)	4-VectorPotential	4-VectorPotenial of a moving point charge (Lienard-Wiechert potential) A_EM = (q/4πε_oc) U / [R·U]_ret [..]_ret implies (R·R = 0, the definition of a light signal) Φ_EM = (γΦ_o) = (γq/4πε_or) a_EM = (γΦ_o/c²)u = (γqμ_o/4πr)u	Scalar Potential and Vector Potential of a stationary point charge Φ_EM = (q/4πε_or) a_EM = 0 Scalar Potential and Vector Potential of a slowly moving point charge (\|v\|<<c implies γ-->1) Φ_EM = (Φ_o) = (q/4πε_or) a_EM = (Φ_o/c²)u = (qμ_o/4π r)u
Q_EM = (E_EM/c, p_EM) = q A_EM = q (Φ_EM/c, a_EM)	4-VectorPotentialMomentum
P_EM = (E/c + qΦ_EM/c, p + qa_EM) = γ m_o(c,u) P_EM = Π = P + qA_EM = m_oU + qA_EM =(H/c,p_EM) = (γm_oc+q Φ_EM/c,γm_ou+q a_EM)	4-Momentum_EM 4-CanonicalMomentum 4-TotalMomentum	Minimal Coupling ============= Total 4-Momentum = Particle 4-Momentum + Potential(Field) 4-Momentum
D = ∂ + iq/ћ A_EM	Minimal Coupling Prescription	KG equation, with minimal coupling to an EM potential D·D = = -(m_oc/ћ)² (∂ + iq/ћ A_EM)·(∂ + iq/ћ A_EM) + (m_oc/ћ)² = 0	Schrödinger Equation (with standard scalar external potential) (i ћ)( ∂_t ) = V[x] - (ћ)²(∇)²/2m_o

E^{2 =}p·p c² + m_o²c⁴: Energy of a particle has a Momentum component and a RestMass component

Final Notes and My Predictions:

Since QM is derivable from SR, this explains why you can't just "Quantize Gravity".

SR is a limiting-case of GR. RQM is directly derivable from SR. QM is a limiting-case of RQM. CM is a limiting-case of QM.
Quantum Mechanics is not a "separate system" from Relativity. It is a special case of SR phenomena.
As such, one cannot assume that SR or QM or SRQM "rules of quantization" apply to the more general GR,
except perhaps in the local tangent spaces which are locally Minkowskian.

This makes sense actually - QM has typically been the science of really small things,
i.e. you have to zoom in to the region for which the SpaceTime is locally flat... → Minkowskian...
The hint for QM has been in the local SR tangent space all along. :)

We should not be looking to "Quantize Gravity", we should be looking to "General Relativize Quantum Mechanics".

Now, for a few of my predictions, based on the SRQM treatise (see List of unsolved problems in physics):
============================================================================

Time:
See GR for the final word on time.
However, even SR gives some interesting perspectives on time.
Examine all possible Lorentz Transformations.
All Lorentz Transforms have an invariant inner-product of 4, due to SpaceTime being 4-dimensional.
All Lorentz Transforms have an invariant determinant of ±1, due to the physical transformations being linear affine.
The positive ones are physical operations, the negative ones are mirror inversions.
The interesting invariant is the trace of Lorentz Transforms, which acts as a sort of identifier.
It can range from negative infinity to positive infinity, but in a special way.

SRQM-LorentzTransforms-TraceIdentification

Examining the various connections leads to a fascinating conclusion! A solution to 2 major unsolved physics problems - see below:

Arrow-of-Time & Baryon Asymmetry Problem (Matter-Antimatter Asymmetry):
SR leads to the idea of a Dual SpaceTime Universe, with a positive flow of time leading to the observed matter-dominated universe,
and with a negative flow of time leading to a dual antimatter-dominated universe on the "other" side of the Big Bang.
Note that this is not showing an antimatter universe contracting into a Big Bang.
The time flow is in both sides AWAY from the Big Bang Creation point.
CPT symmetry, the Feynman-Stueckelberg interpretation of antiparticles, and lack of observation of large scale antimatter leads to this conclusion
Mystery Deepens: Matter and Antimatter Are Mirror Images (Aug 015)):

Interpretation of QM:
Many-Worlds is simply wrong (Occam's razor).
Copenhagen is great for calculation but wrong in trying to separate microscopic from macroscopic.
Relational QM is the closest to this SRQM Interpretation of QM.

Theory of Everything/GUT:
See Coleman-Mandula Theorem,

SpaceTime Symmetry	Internal Particle Symmetries
SL(2,ℂ) ⋉ ℝ^1,3	U(1)	SU(2)	SU(3)
Gravity	EM	Weak	Color
GR	Standard Model (QM)

The problem with "Quantum Gravity" is that people are trying to figure out the "Internal Particle Symmetry" of GR, which doesn't fit into that category. It already has a symmetry group, that of Double Cover of the Poincare group.

This is the new paradigm... based on SRQM...

Physical Information:
Is an observer-based phenomenon.
The information about the state of a system, the observer's wavefunction information, can be "different" for different observers, while the system itself remains independent of what the observer does non-locally.
Put one "protected" scientist observer inside the box with the cat, and one observer outside the box.
|cat> = |alive>.
Close the box.
The inside observer continues seeing |cat> = |alive> until the randomly timed death event, upon which the observer will then see |cat> = |dead>.
The outside observer immeadiately gets |cat> = 1/Sqrt[2]*(|alive> + |dead>) when the lid is closed, and continues seeing this until the box is again opened.
The cat only ever observes |cat> = |alive>.
The person who lost the cat in the first place when it wandered away into the scientists' box only ever sees |cat> = 1/Sqrt[2]*(|alive> + |dead>), regardless of the state of the box lid.
Really, that person has information more like |cat> = |lost>, and it remains that way unless that cat can escape and return home.
Closing the box physically does nothing to the cat. It only changes the information available to the various on-site observers.

Black Hole Information Paradox:
The answer is actually pretty simple.
Consider the Binary BH and NS mergers that have been detected so far:
Analysis of the gravitational waves allowed one to figure out the approximate masses and spins of the initial pair and final single.
Now, consider something smaller "falling into" a black hole, perhaps a planet. This should generate gravitational waves also, which carry information.
Now, consider something smaller "falling into" a black hole, perhaps an asteroid. This should generate gravitational waves also, which carry information.
Now, consider something smaller "falling into" a black hole, perhaps a speck of dust. This should generate gravitational waves also, which carry information.
Now, consider something smaller "falling into" a black hole, perhaps a single particle. This should generate gravitational waves also, which carry information.
Ta-da! Conservation of information. Information about a particle falling into the BH is encoded in the gravitational waves generated by the event, which then travel out to ... the universal horizon.
The particle then becomes one with the BH, with no more information left - just BH entropy.
Finally, a way that the holographic principle makes a little sense - just not in the way it is usually presented.
So, when one wanders up to a black hole and asks where all the information is; the answer is that all the info is rushing away to the edges of the universe in the form of gravitational waves.
It didn't just vanish from reality.
Of course, the newly enlarged BH still retains its info concerning its rest mass, intrinsic spin, EM charge, it's 4-Position and 4-Velocity.
Or, you can combine the rest mass and 4-Velocity into its 4-Momentum.
So, all the worry about information loss from Hawking Radiation is resolved.
The information is stored in gravitational waves which radiate away in the collapse stage.
The later Hawking Radiation is random blackbody, and carries no info.
So, yes, black holes have entropy. But, all the information about the original bodies is radiated away in the form of GW's during BH formation.
There is no further information to "lose" during BH evaporation / Hawking Radiation.
See also: No Hair Theorem, enforced by Price's Theorem.
Price's Theorem, contained within Kerr BlackHole summary

Fine-tuned Universe:
The constants in this universe seem pretty good for carbon-based life. If the constants were different, there would likely be some other form of "life" (i.e. non-carbon-based).
No need for an anthropmorphic principle.

Cosmology Stuff:
A lot of this is probably really just too early to tell for sure... but GR is your best shot.

The Discrepancy between Quantum Vacuum Energy and the GR Vacuum Energy by up to 120 orders of magnitude:
GR is correct. QM is a locally Minkowskian phenomenon, it doesn't apply.
The Casimir Effect and the Quantum Vacuum (Jaffe 2005),
--In discussions of the cosmological constant, the Casimir effect is often invoked as decisive evidence that the zero point energies of quantum fields are"real''. On the contrary, Casimir effects can be formulated and Casimir forces can be computed without reference to zero point energies. They are relativistic, quantum forces between charges and currents. The Casimir force (per unit area) between parallel plates vanishes as α, the fine structure constant, goes to zero, and the standard result, which appears to be independent of α, corresponds to the α→∞ limit,

Missing Mass in Universe:
GR, with a cosmological constant, can account for observations.

Dark Matter:
Likely to be purely a GR phenomenon - Right now the middle-weight Black Holes found by LIGO seem to be pretty good candidates. i.e. "Dark Matter" = Black Holes.
Alternately, it could be a type of GR mass particle, which does not interact with any of the U(1)=EM, SU(2)=Weak, or SU(3)=Color symmetries.
In other words, a purely "mass" particle. An event which has rest mass but no charge of any type.
If so, then the current types of detectors would not see them.
Also, such a GR mass particle would not be a black hole, since it would not carry or interact with EM charge.
You might also call them NOCT particles, (Not Otherwise Charged Trace) particles, with "Noct-" being the Latin root for "Night". :)
Night Particles, Dark Matter.
see
Science News (Jan 2017): Dark matter still missing,
Scientific America (Nov 2017): dark-matter-hunt-fails-to-find-the-elusive-particles,
Nature (Nov 2017): dark-matter-hunt-fails-to-find-the-elusive-particles,

Dark Energy:
Again, purely GR - The Cosmological Constant fits the bill pretty well.

Vacuum Catastrophe:
QM is a limiting-case approximation of GR. Infinities, etc. arise from assuming that QM is fundamental and trying to impose "classical" results on GR.
An analogous situation would be taking the classical velocity relation v₁₂ = v₁ + v₂ and t

Quantum Mechanics (QM) derived from Special Relativity (SR) The RoadMap to the SRQM Interpretation of Quantum Mechanics A Study of Physical 4-Vectors, Tensors, and Lorentz Invariants

Roadmap from Special Relativity to Quantum Mechanics: (The Short Version)

This is the old paradigm...

This is the new paradigm, based on the SRQM interpretation.

Basics

References

Justification of the SRQM treatise

SR Light Cone

SR 4-Vectors - Notation, Conventions, Properties

Standard Physical SR 4-Vectors

Standard Physical SR 4-Tensors

Standard Physical SR 4-Vector References

Standard Physical SR 4-Vector Properties

Standard Physical SR 4-Vector Relations (Physical Laws)

Scalar Products and other SR 4-Vector Relations (Physical Laws)

SR Light Cone

Quantum Mechanics from SR 4-Vector Relations

More SR Physical 4-Vectors

Potentials/Fields:

PotentialMomentum:

SpaceTime Lattice, Lorentz Invariant Quantization, Radial Standing-Wave Hypotreatise, Quantum Jumps, Angular Momentum

The Dirac Equation Derived

Photon Polarization

CPT & SR Phase Connection, and eventually the Spin-Statistics Theorem

Lagrangian/Hamiltonian Formalisms:

More on the Group Properties of Minkowski Space → Poincaré Group from "Representations of the Symmetry Group of SpaceTime" by Kyle Drake, Michael Feinberg, David Guild, Emma Turetsky

Identical Particles:

Covariant Commutation Relations:

Everyday Special Relativistic Effects

Some more Tensor Stuff

Derived Equations and Newtonian Limts:

Final Notes and My Predictions:

Quantum Mechanics (QM) derived from Special Relativity (SR)
The RoadMap to the SRQM Interpretation of Quantum Mechanics
A Study of Physical 4-Vectors, Tensors, and Lorentz Invariants

More on the Group Properties of Minkowski Space → Poincaré Group
from "Representations of the Symmetry Group of SpaceTime" by Kyle Drake, Michael Feinberg, David Guild, Emma Turetsky