John's Science, Math, Philosophy Stuff:
The Science Realm: John's Virtual Sci-Tech Universe | 4-Vectors | Ambigrams | Antipodes | Covert Ops Fragments | Cyrillic Projector | Forced Induction (Sums Of Powers Of Integers) | Fractal Tree | Frontiers | IFS Fractals (Assembly) | IFS Fractals (Javascript) | JavaScript Graphics | Kid Science | Kryptos | Philosophy | Photography | Physics-Planck Constant Measurement Via LEDs | Prime Sieve | QM from SR | QM from SR-Simple RoadMap | QM from SR-Simple RoadMap (PDF) | SR 4-Vector & Tensor Calculator |Quantum Phase | Quotes | RuneQuest Cipher Challenge | Secret Codes & Ciphers | Scientific Calculator (complex capable) | Science+Math | Sci-Pan Pantheist Poems | Stereograms | SuperMagicSqr4x4 |Turkish Grammar |Melike Wilson Art
Site last modified: 2021-Aug
Welcome to Relativistic Quantum Reality: Virtual worlds of imaginary particles: The dreams stuff is made of: Life, the eternal ghost in the machine...
This site is dedicated to the quest for knowledge and wisdom, through science, mathematics, philosophy, invention, and technology.
May the treasures buried herein spark the fires of imagination like the twinkling jewels of celestial light crowning the midnight sky...
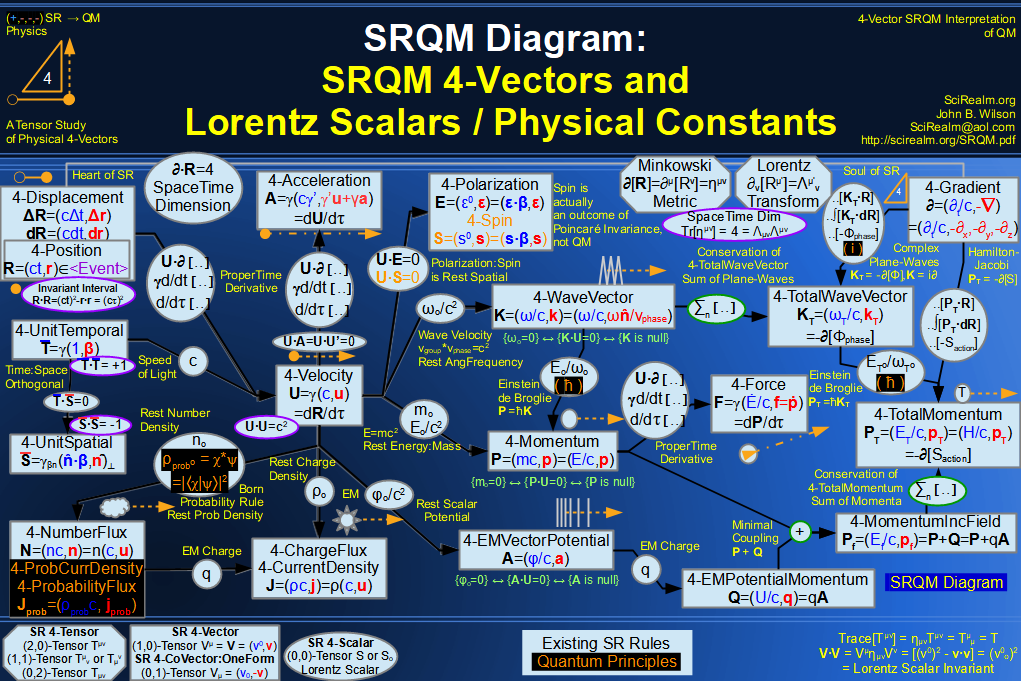
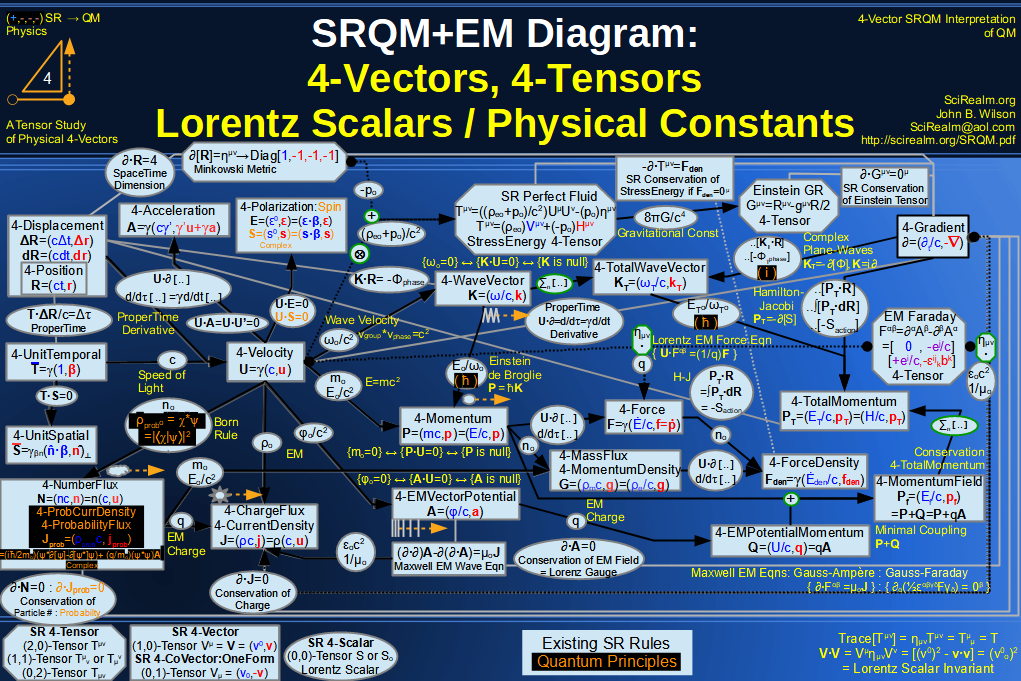
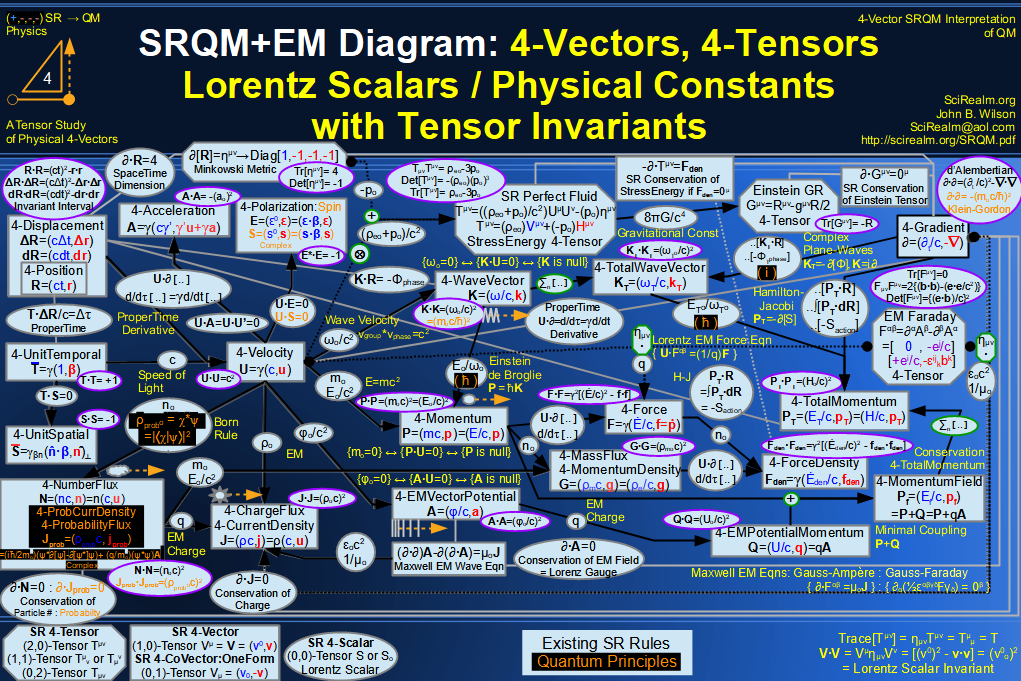
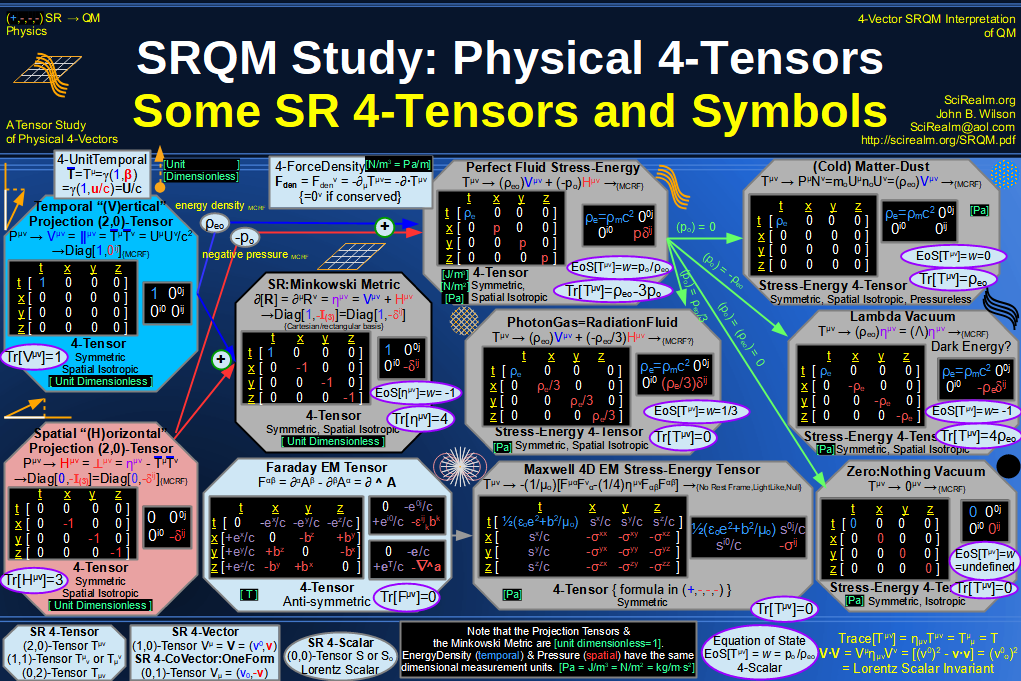
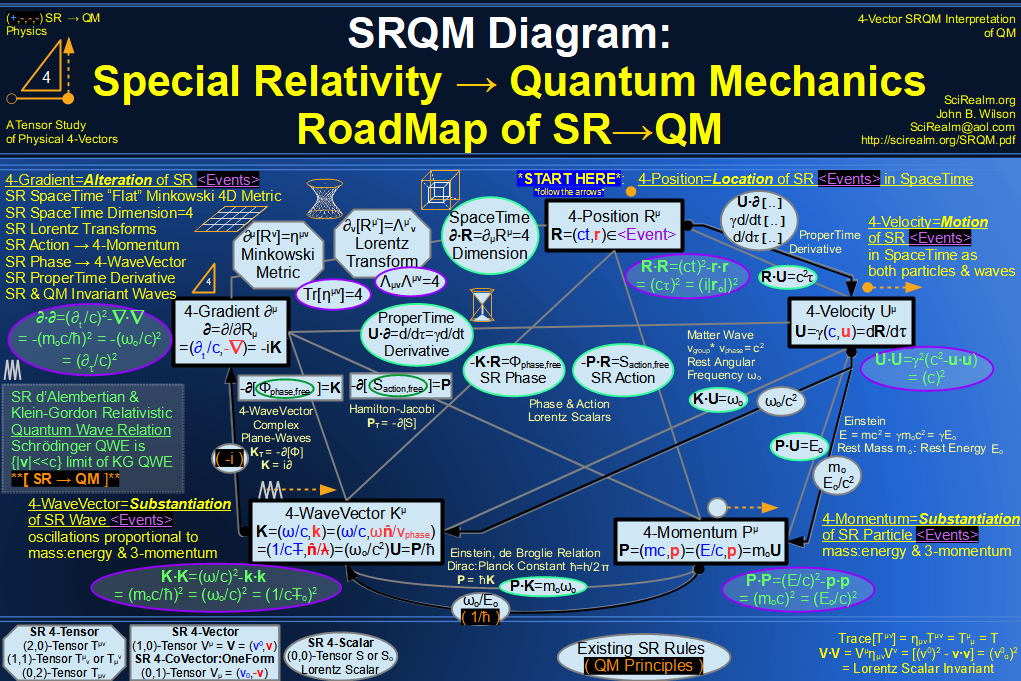
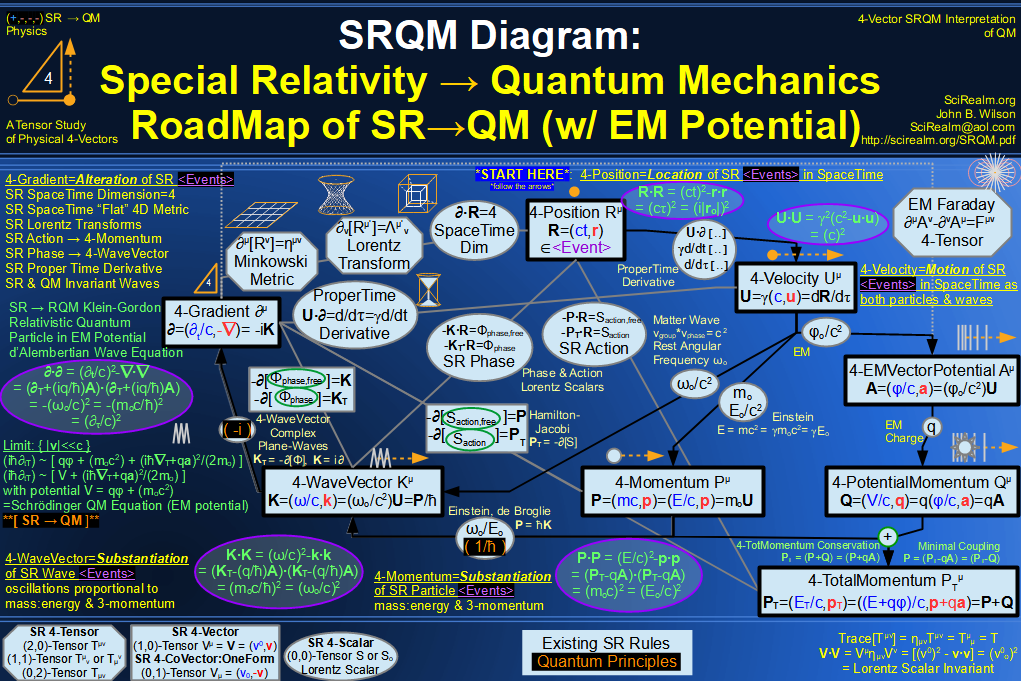
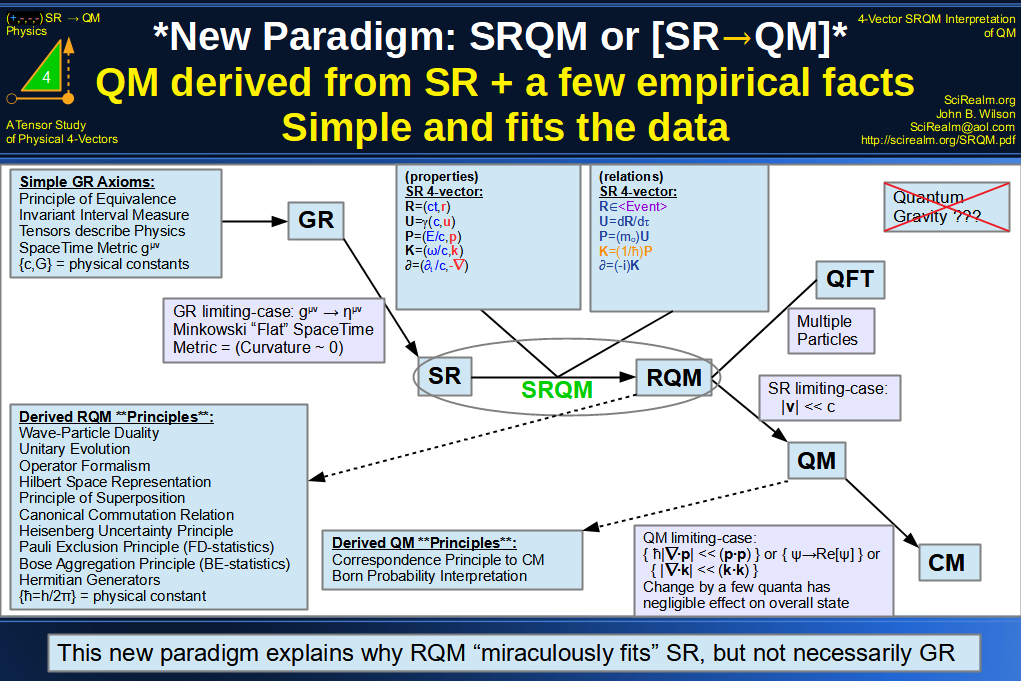
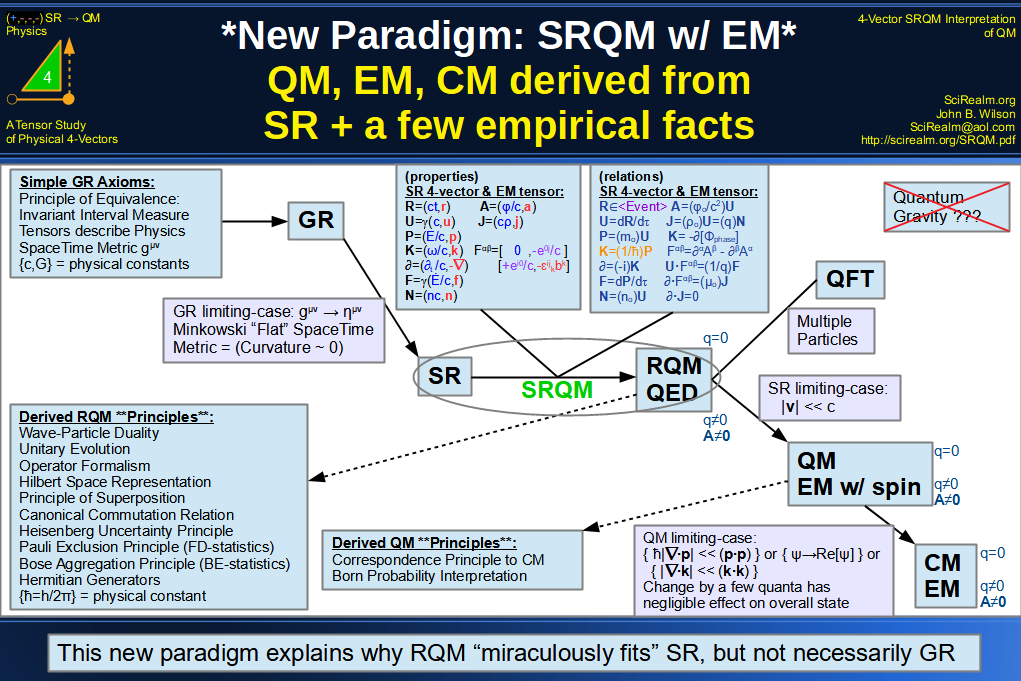
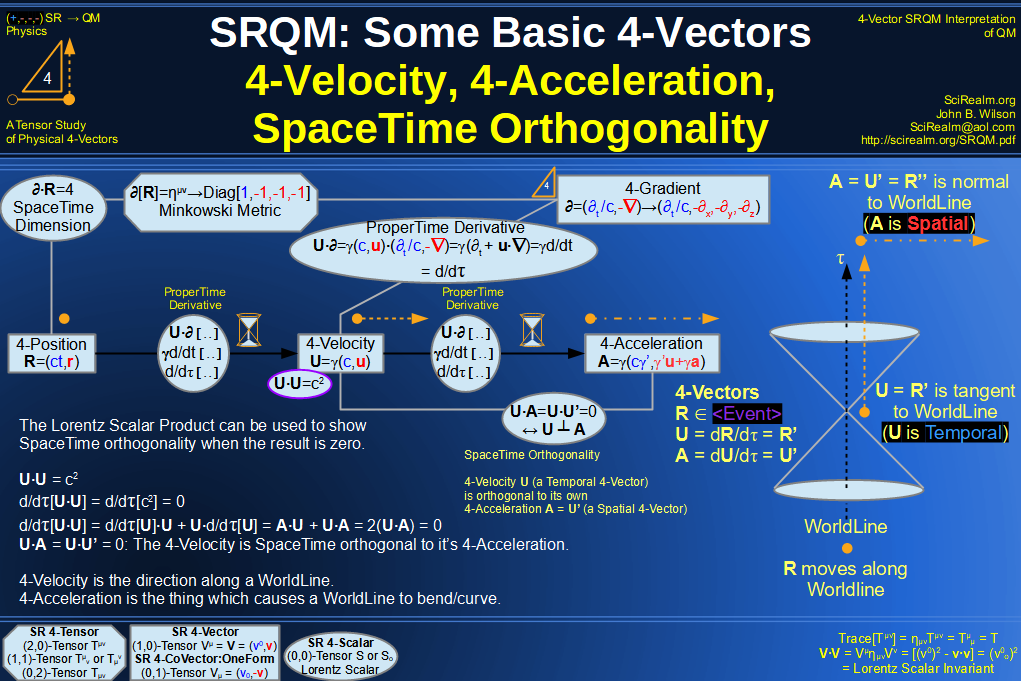
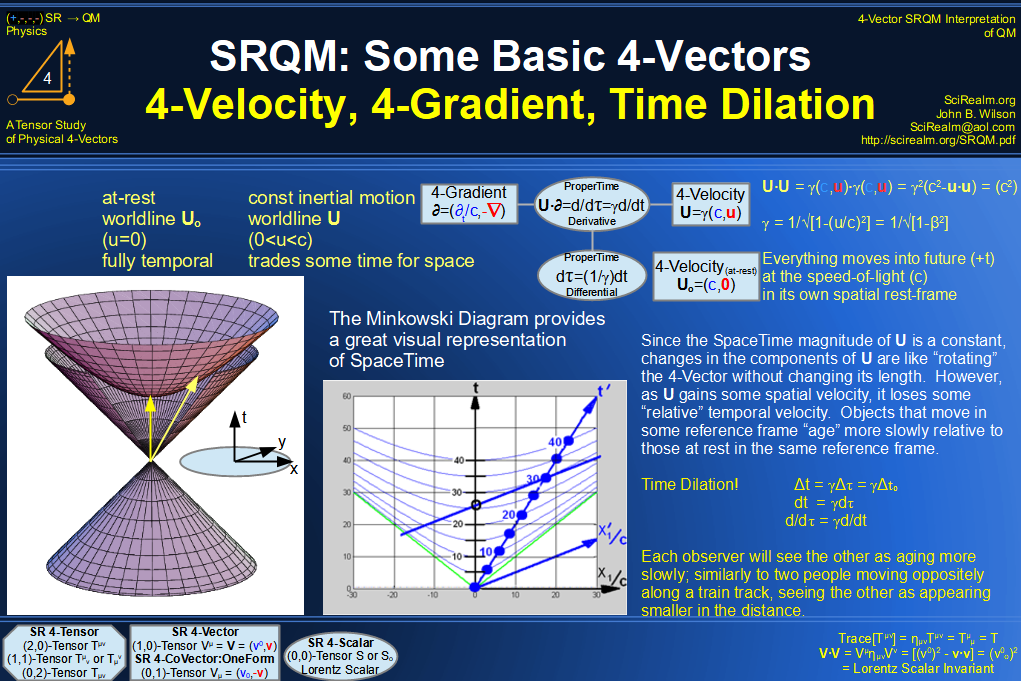
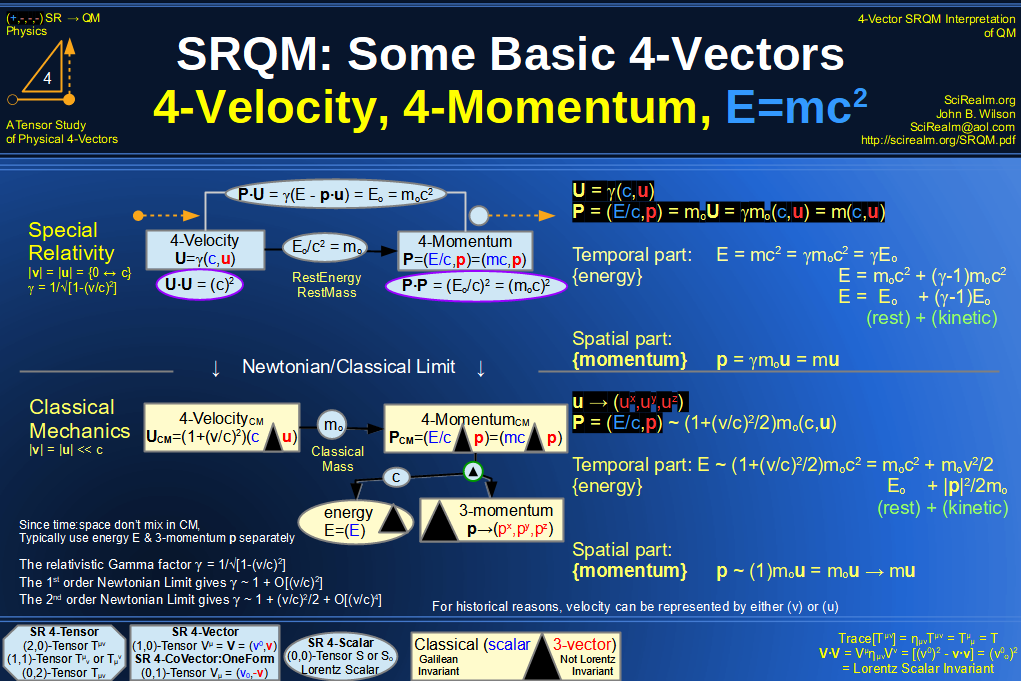
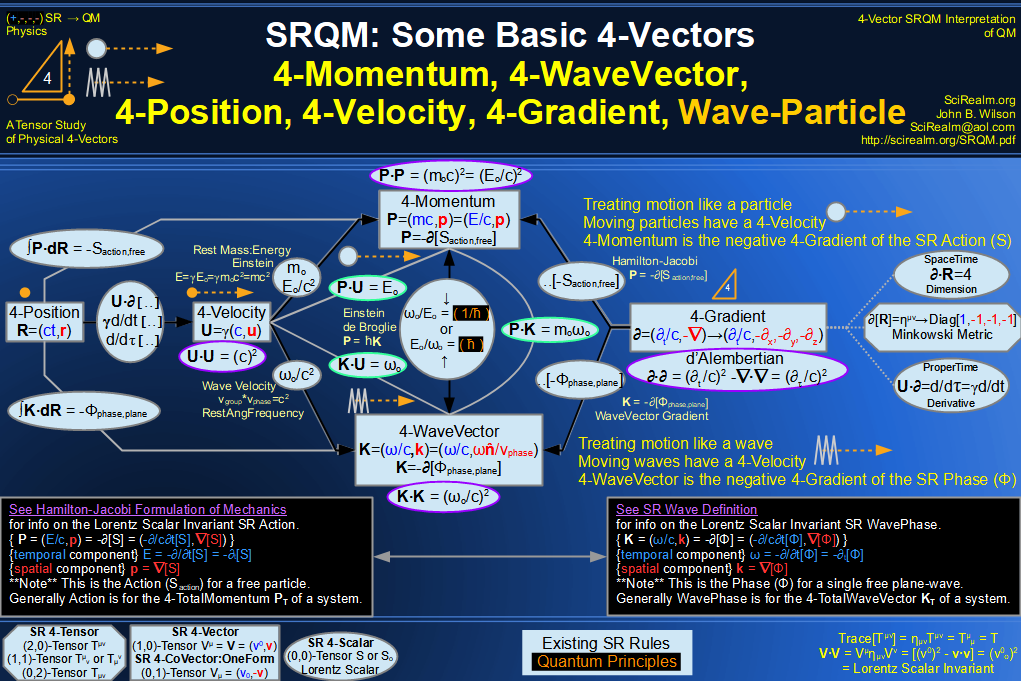
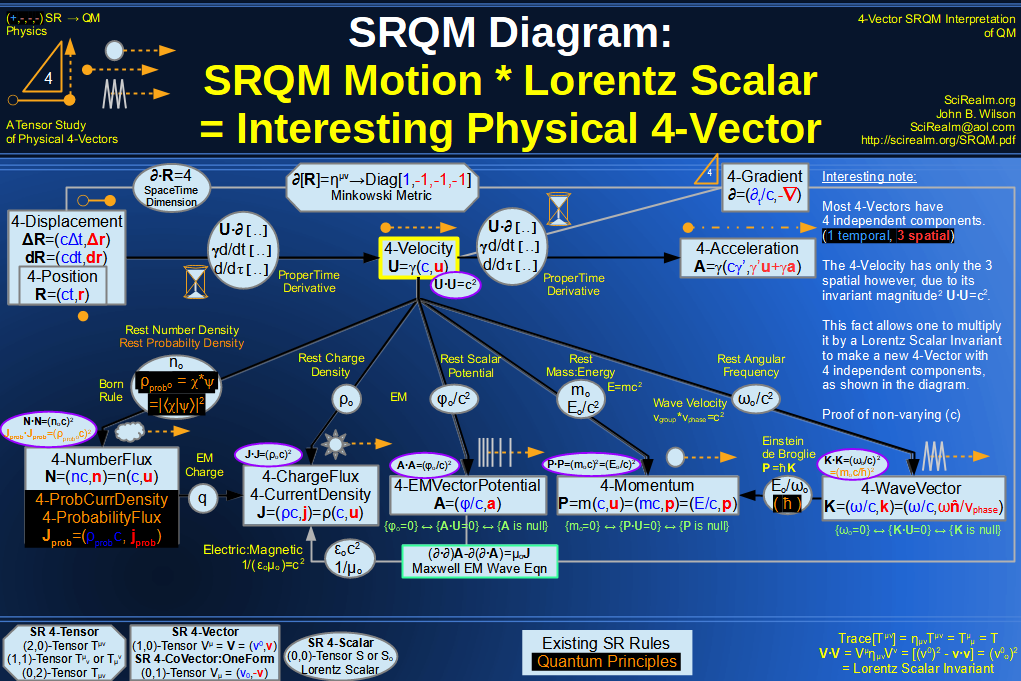
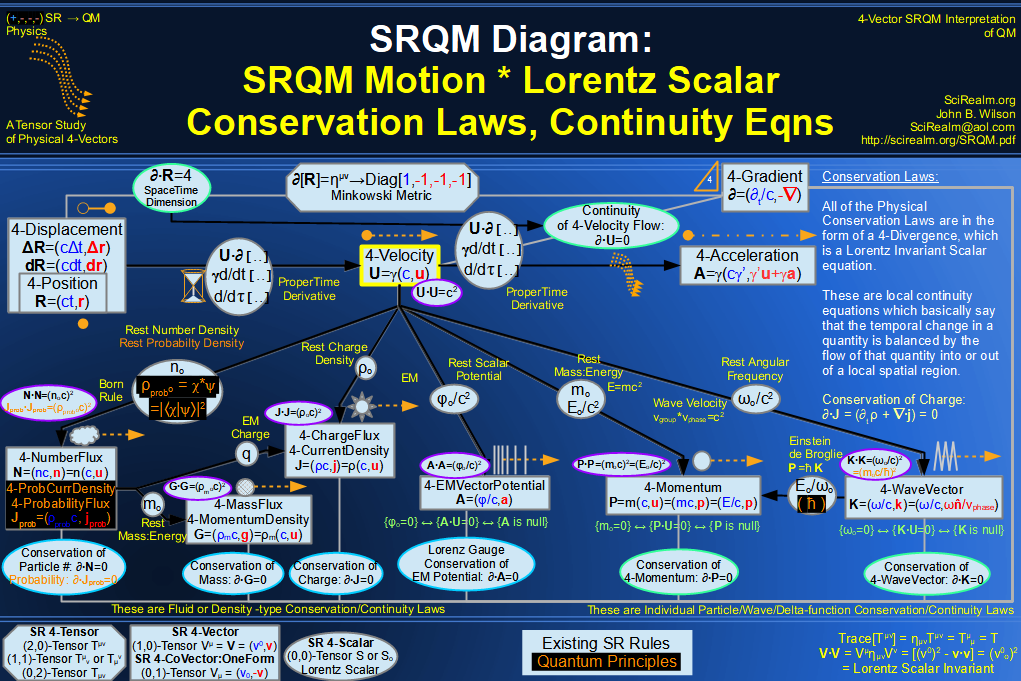
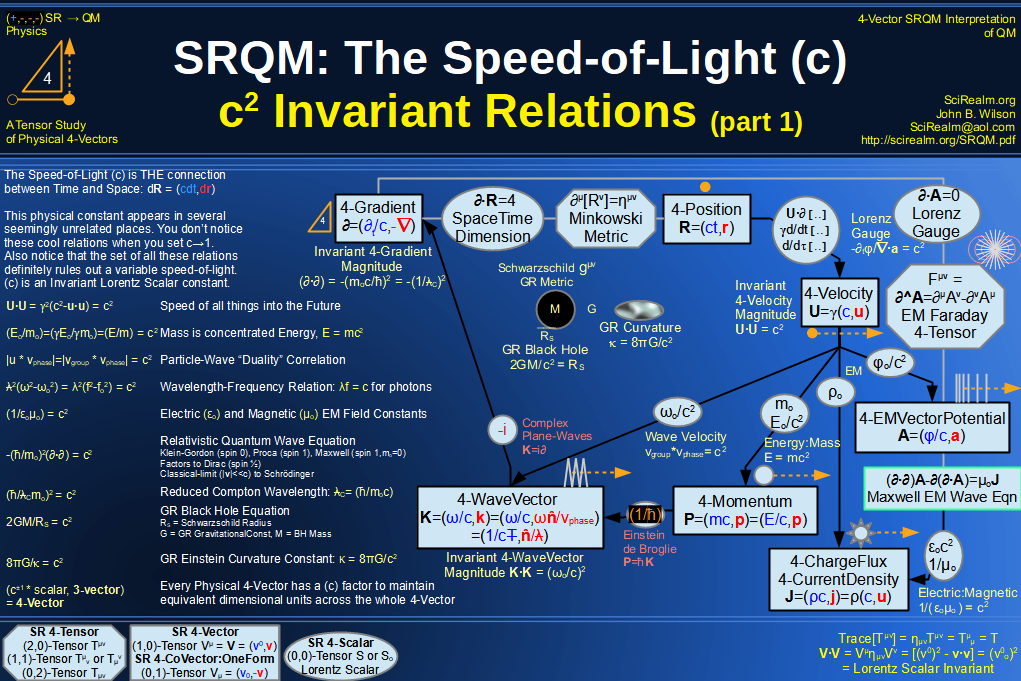
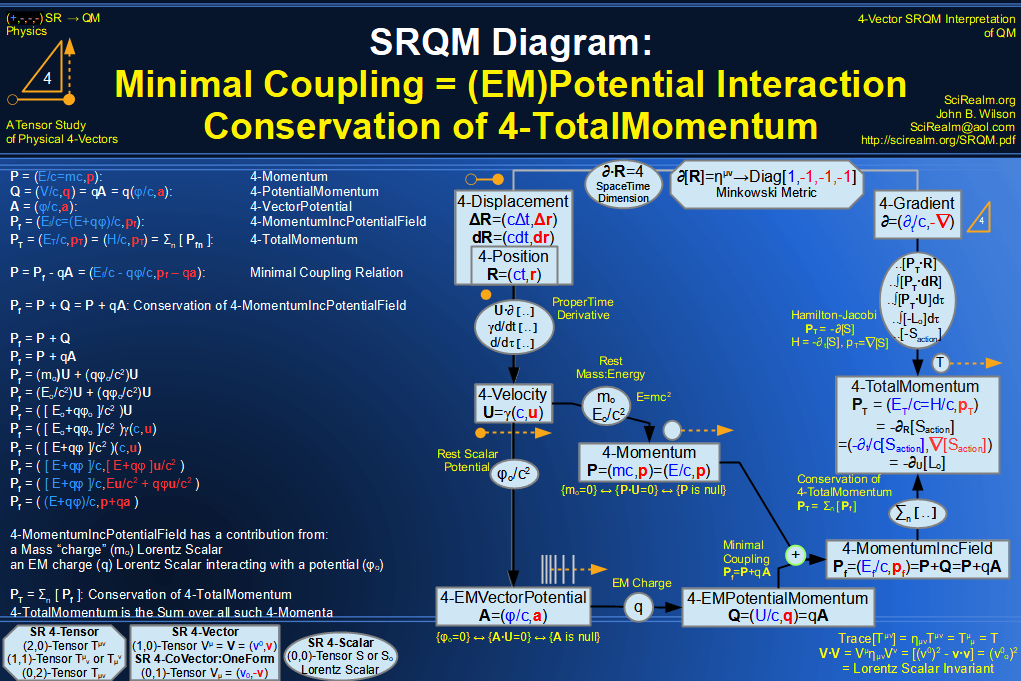
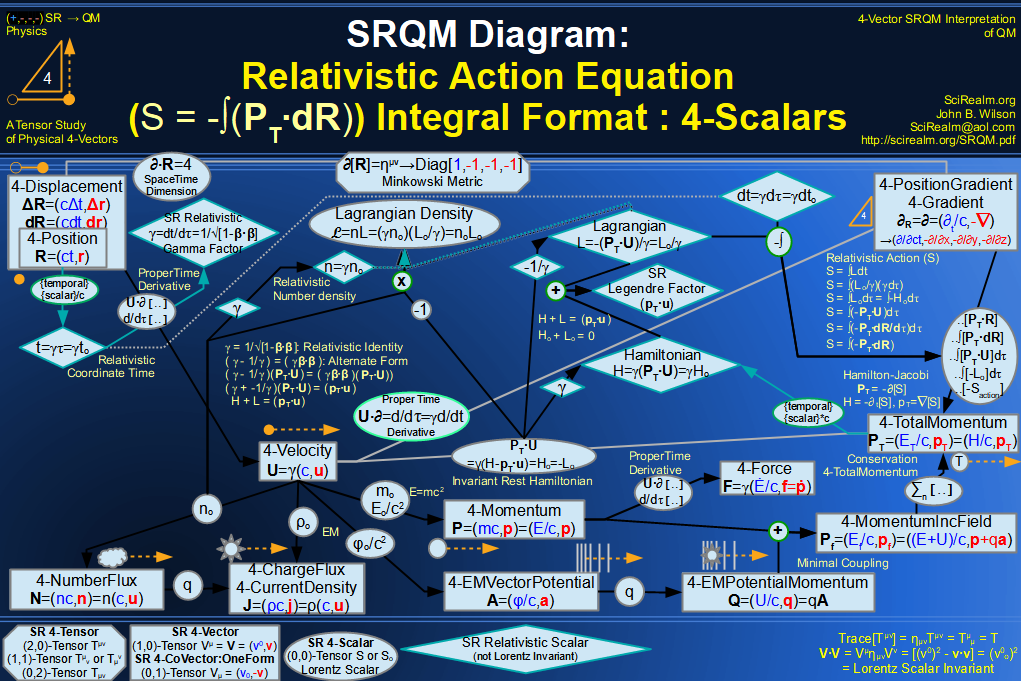
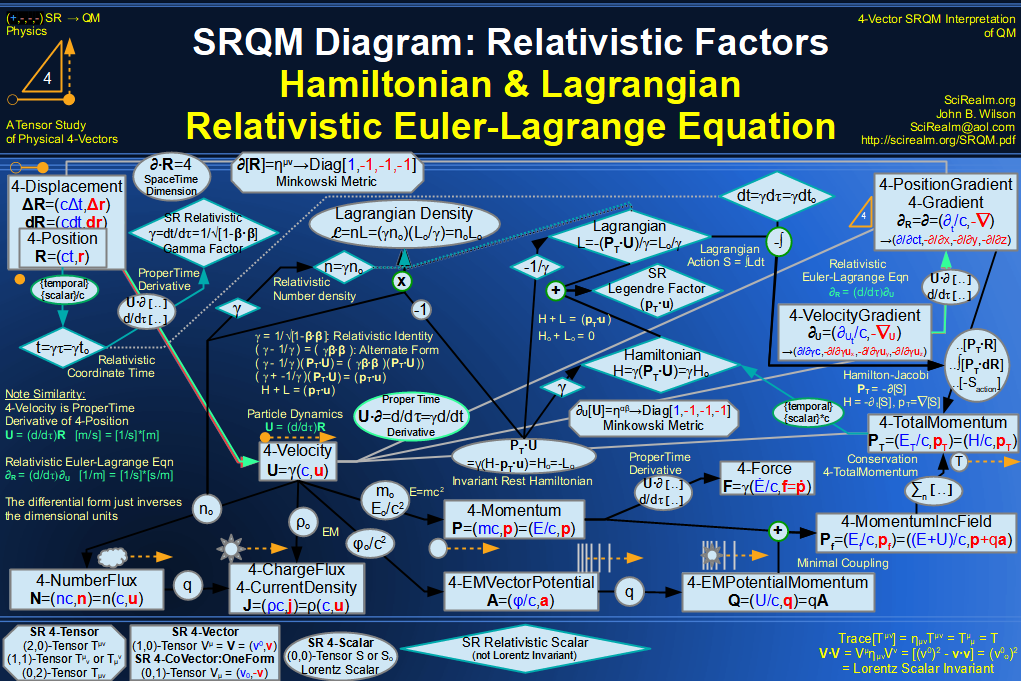
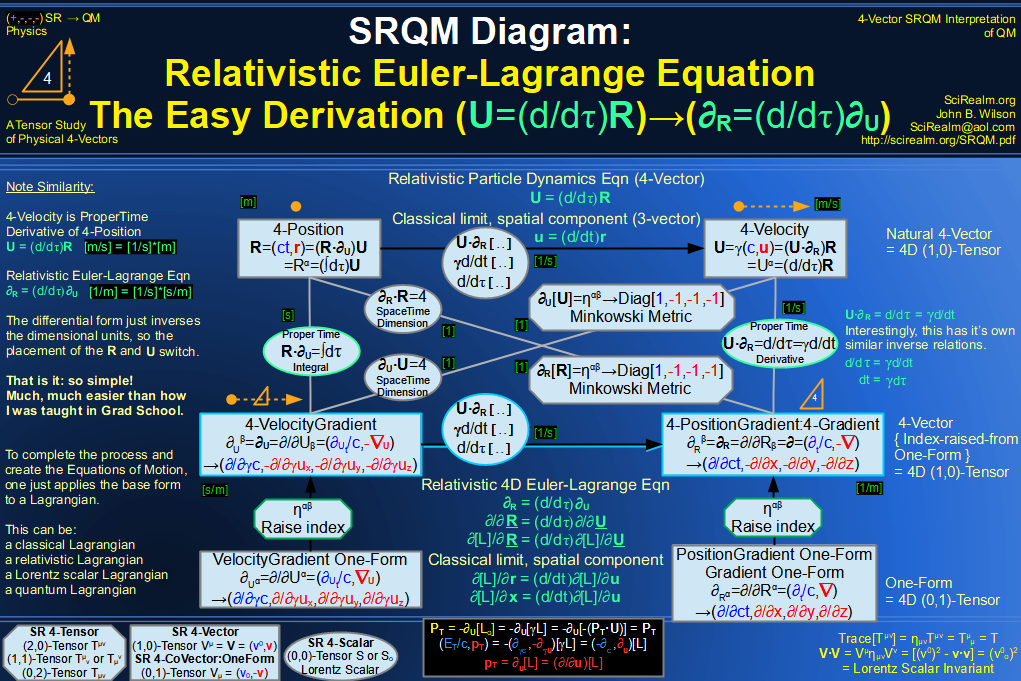
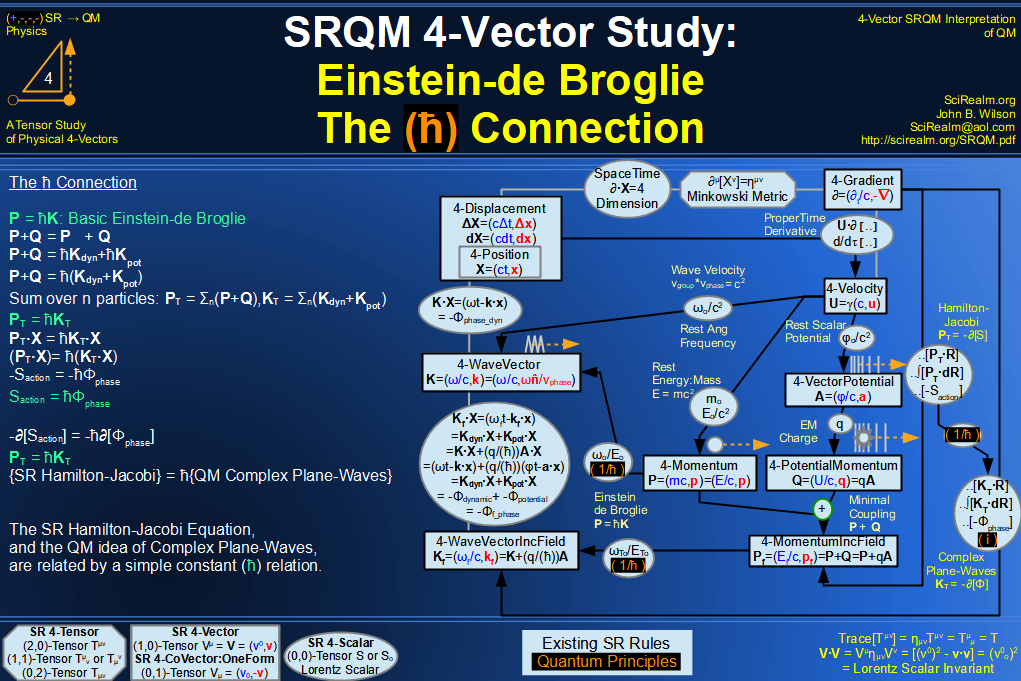
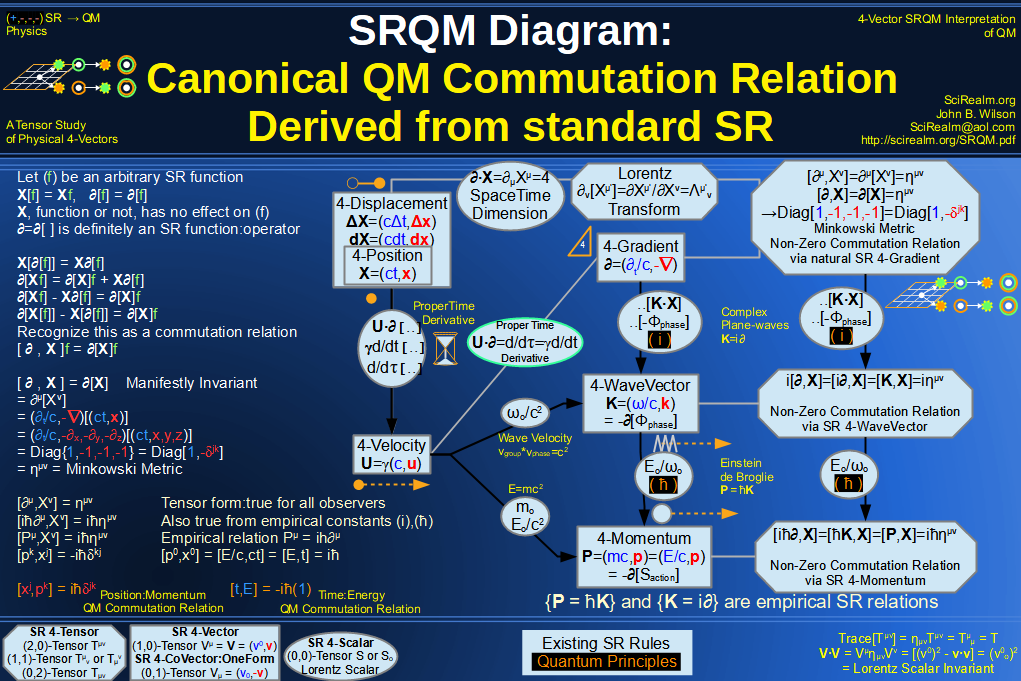
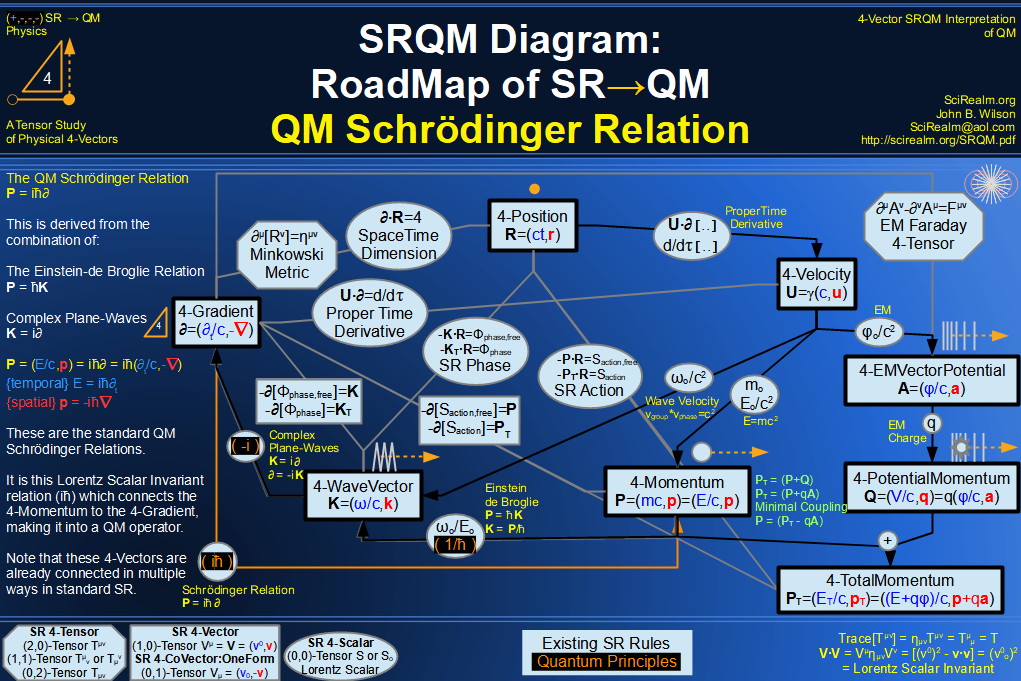
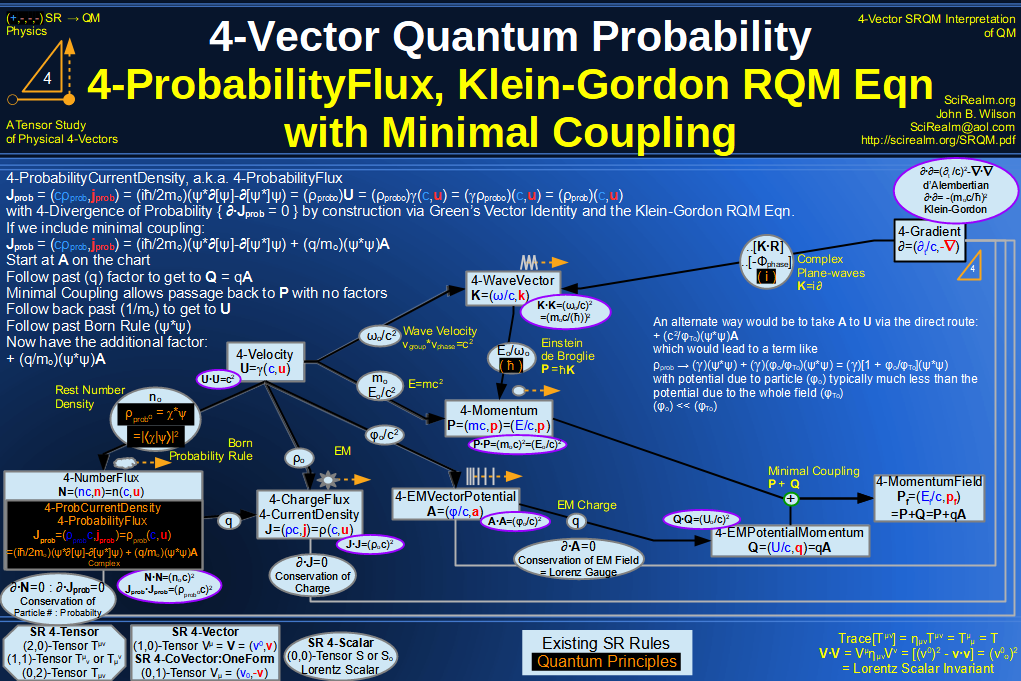
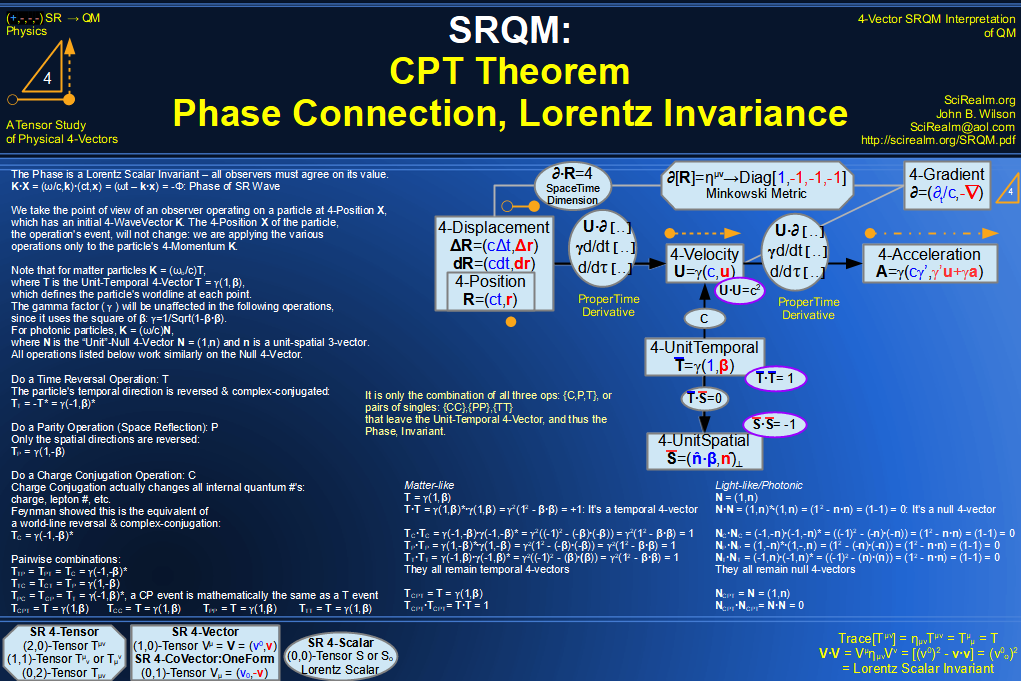
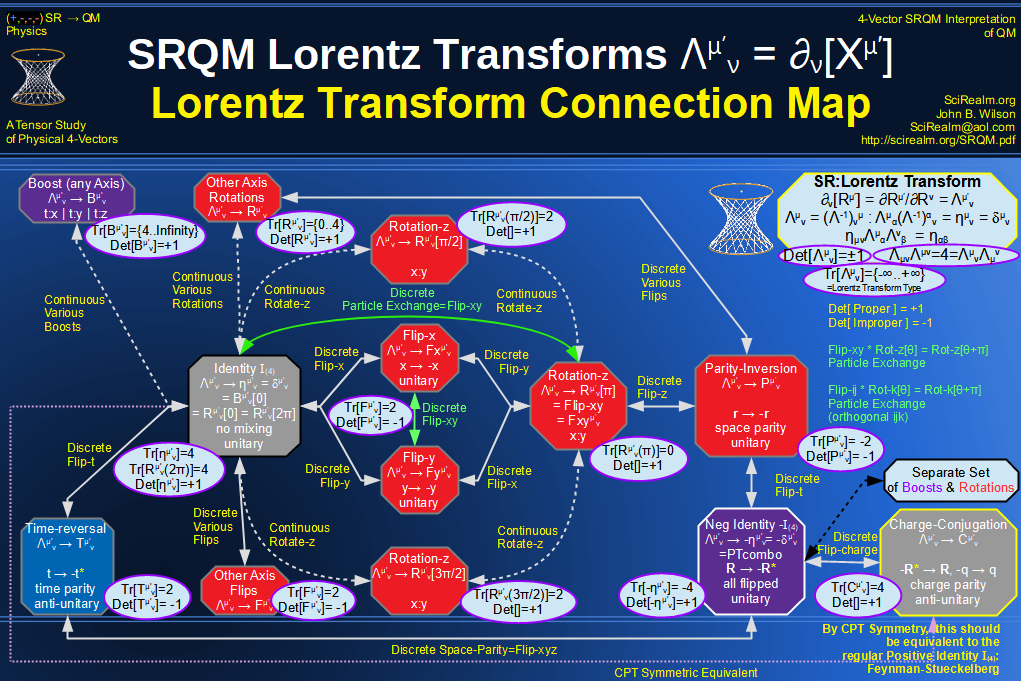
Quantum Mechanics is derivable from Special Relativity
See SRQM - QM from SR - Simple RoadMap (.html)
See SRQM - QM from SR - Simple RoadMap (.pdf)
See SRQM - Online SR 4-Vector & Tensor Calculator
See Online Complex-capable RPN Scientific Calculator
***Learn, Discover, Explore***