Lagrangian/Hamiltonian Formalisms:
see Relativistic Lagrangian Mechanics
Relativistic Beta Factor β = u/c
Relativistic Gamma Factor γ = 1/√[1-β2]
The whole Lagrangian/Hamiltonian connection is given by the relativistic identity:
γ = 1/√[1 - β2]
γ2 = 1/(1 - β2)
(1 - β2)γ2 = 1
(γ2 - γ2β2) = 1
(γ2 - 1) = γ2β2
( γ - 1/γ ) = (γβ2)
Now multiply by your favorite Lorentz Scalars... In this case for a
free relativistic particle...
( γ - 1/γ )(P·U) = ( γβ2)(P·U)
( γ - 1/γ )(moc2) = ( γβ2)(moc2)
( γmoc2 - moc2/γ ) = γmoc2β2
( γmoc2 - moc2/γ ) = γmou2
( γmoc2) + (- moc2/γ ) = γmou·u
( γmoc2) + (- moc2/γ ) = (p·u)
( H ) + ( L ) = (p·u)
The Hamiltonian/Lagrangian connection falls right out.
Note that neither (H) nor (L) are scalar invariants, due to the extra (γ) factors.
Now, including the effects of a potential:
4-VectorPotential A = (φ/c,a)
{ = (φEM/c,aEM) for EM potential }
4-PotentialMomentum Q = qA due to 4-VectorPotential acting on charge (q)
4-TotalMomentum of System PT = P + Q = P + qA = moU + qA
= (H/c,pT) = (γmoc + qφ/c,γmou + qa)
A·U = γ(φ - a·u) = φo
P·U = γ(E - p·u) = Eo
PT·U = Eo + qφo = moc2 + qφo
I assume the following as a valid SR relation:
A = (φo/c2)U = (φ/c,a)
= (φo/c2)γ(c,u) = ((γφo/c),
(γφo/c2)u) giving (φ = γφo and a
= (γφo/c2)u)
This is analogous to P = (Eo/c2)U
( γ - 1/γ )(PT·U) = ( γβ2)(PT·U)
γ(PT·U) + -(PT·U)/γ
= ( γβ2)(PT·U)
γ(PT·U) + -(PT·U)/γ
= (pT·u)
( H ) + ( L ) = ( pT·u )
Relativistic
Hamiltonian
H = γ(PT·U) |
Relativistic
Lagrangain
L = -(PT·U)/γ |
pT·u = ( γβ2)(PT·U) =
H + L =
γ(PT·U) + -(PT·U)/γ |
H = γ(PT·U)
H = γ((P + Q)·U)
H = γ(P·U + Q·U)
H = γP·U + γQ·U
H = γmoU·U + γqA·U
H = γmoc2 + qγφo
H = γmoc2 + qφ
H = ( γβ2 + 1/γ )moc2 + qφ
H = ( γmoβ2c2 + moc2/γ) + qφ
H = ( γmou2 + moc2/γ) + qφ
H = p·u + moc2/γ + qφ
H = E + qφ
H = ±c√[mo2c2 + p2] + qφ
H = ±c√[mo2c2 + (pT -qa)2] + qφ
H = ±moc2√[1 + (pT -qa)2/(mo2c2)] + qφ |
L = -(PT·U)/γ
L = -((P + Q)·U)/γ
L = -(P·U + Q·U)/γ
L = - P·U/γ - Q·U/γ
L = -moU·U/γ - qA·U/γ
L = -moc2/γ - qA·U/γ
L = -moc2/γ - q(φ/c,a)·γ(c,u)/γ
L = -moc2/γ - q(φ/c,a)·(c,u)
L = -moc2/γ - q(φ - a·u)
L = -moc2/γ - qφ + qa·u
L = -moc2/γ - qφo/γ
L = -(moc2 + qφo)/γ |
H + L = γ(PT·U) - (PT·U)/γ
H + L = (γ - 1/γ)(PT·U)
H + L = ( γβ2)(PT·U)
H + L = ( γβ2)((P + Q)·U)
H + L = ( γβ2)(P·U + Q·U)
H + L = ( γβ2)(moc2 + qφo)
H + L = (γmoβ2c2 + qγφoβ2)
H + L = (γmou·uc2/c2 + qφoγu·u/c2)
H + L = (γmou·u + qa·u)
H + L = (p·u + qa·u)
H + L = pT·u |
Rest Hamiltonian
Ho = (PT·U) = H/γ |
Rest Lagrangain
Lo = -(PT·U) = γL |
Ho + Lo = 0 |
The non-relativistic Hamiltonian Hnon-rel is an approximation of the relativistic Hamiltonian H:
H = γ(moc2 + qφo)
H = (1/√[1-(v/c)2])(moc2 + qΦo)
~ [1 + (v/c)2/2])(moc2 + qφoEM)
= (moc2 + qφo) + (1/2)(moc2v2/c2
+ qφov2/c2) ~ (moc2
+ qφo) + (1/2)(mov2 + 0)
H ~ (1/2)(mov2) + (moc2
+ qφo)
H ~ (Kinetic) + (Rest + Potential) = T + V {for |v| << c}
Hnon-rel = T + V
The non-relativistic Lagrangian Lnon-rel is an approximation of the relativistic Lagrangian L:
L = -(moc2 + qφo)/γ
-L = (moc2 + qφo)/γ = √[1-(v/c)2](moc2
+ qφo) ~ (moc2 + qφo)
- (1/2)(moc2v2/c2 + qφov2/c2)
~ (moc2 + qφo) - (1/2)(mov2
+ ~0 )
L ~ (1/2)(mov2) - (moc2 + qφo)
L ~ (Kinetic) - (Rest + Potential) = T - V {for |v| << c}
Lnon-rel = T - V
Thus, (H ~ T + V = Hnon-rel ) and (L ~ T - V = Lnon-rel ) only in the non-relativistic limit (|v| << c)
H + L ~ (T + V) + (T - V) = 2T = 2 (1/2 mou·u) = p·u
Thus, ( H ) + ( L ) = (p·u) is always true, in both the relativistic and non-relativistic case.
H = ± moc2√[1 + (pT -qa)2/(mo2c2)] + qφ
H ~ ± moc2[1 + (pT -qa)2/(2mo2c2)] + qφ for |(pT -qa)2/(moc)2| << 1
H ~ ± [moc2 + (pT -qa)2/(2mo)] + qφ for |(pT -qa)2/(moc)2| << 1 {non-relativistic limit}
Let's now show that the Schrödinger equation is just the low energy limit of the Klein-Gordon equation.
We now let the Klein-Gordon equation use the Total Gradient, so now our wave equation uses EM potentials.
D·D = -(moc/ћ)2(∂ + iq/ћA)·(∂+ iq/ћA) + (moc/ћ)2 = 0
letA' = (iq/ћ)A
let M = (moc/ћ)
then (∂ +A')·(∂ +A') + (M)2 = 0
∂·∂ +∂·A' + 2A'·∂ +A'·A' + (M)2 = 0
now the trick is that factor of 2, it comes about by keeping track of tensor notation...
a weakness of strict 4-Vector notation
let the 4-Vector potential be a conservative field, then∂·A = 0
(∂·∂) + 2(A'·∂) + (A'·A') +(M)2 = 0
expanding to temporal/spatial components...
( ∂t2/c2-∇·∇ ) +2(φ'/c ∂t/c -a'·∇ ) + ( φ'2/c2-a'·a') + (M)2 = 0
gathering like components
( ∂t2/c2 + 2φ'/c ∂t/c+ φ'2/c2 ) - (∇·∇ +2a'·∇ + a'·a' ) + (M)2 = 0
( ∂t2 + 2φ'∂t + φ'2 )- c2(∇·∇ + 2a'·∇ + a'·a') + c2(M)2 = 0
( ∂t + φ' )2 - c2(∇ +a')2 + c2(M)2 = 0
multiply everything by (i ћ)2
(i ћ)2( ∂t + φ' )2 - c2(i ћ)2(∇+a' )2 + c2(iћ)2(M)2 = 0
put into suggestive form
(i ћ)2( ∂t + φ' )2 = - c2(iћ)2(M)2 + c2(i ћ)2(∇+a' )2
(i ћ)2( ∂t + φ' )2 = i2c2(iћ)2(M)2 + c2(i ћ)2(∇+a' )2
(i ћ)2( ∂t + φ' )2 = i2c2(iћ)2(M)2 [1 + c2(i ћ)2(∇+a' )2/ i2c2(iћ)2(M)2 ]
(i ћ)2( ∂t + φ' )2 = i2c2(iћ)2(M)2 [1 + (∇ +a')2/ i2(M)2 ]
take Sqrt of both sides
(i ћ)( ∂t + φ' ) = ic(i ћ)(M) Sqrt[1 + (∇ +a' )2/ i2(M)2]
use Newtonian approx Sqrt[1+x] ~ ±[1+x/2] for x<<1
(i ћ)( ∂t + φ' ) ~ ic(i ћ)(M) ±[1 + (∇ +a' )2/2 i2(M)2]
(i ћ)( ∂t + φ' ) ~ ±[ic(i ћ)(M) + ic(i ћ)(M)(∇+a' )2/2 i2(M)2]
(i ћ)( ∂t + φ' ) ~ ±[c(i2 ћ)(M) + c( ћ)(∇+a' )2/2(M) ]
remember M = moc/ћ
(i ћ)( ∂t + φ' ) ~ ±[c(i2 ћ)(moc/ћ)+c( ћ)(∇ +a' )2/2(moc/ћ)]
(i ћ)( ∂t + φ' ) ~ ±[c(i2)(moc) +(ћ)2(∇ +a' )2/2(mo)]
(i ћ)( ∂t + φ' ) ~ ±[-(moc2) +(ћ)2(∇ +a' )2/(2mo)]
remember A'EM = iq/ћAEM
(i ћ)( ∂t + iq/ћφ ) ~ ±[-(moc2) +(ћ)2(∇ + iq/ћa )2/2mo]
(i ћ)( ∂t ) + (i ћ)(iq/ћ)(φ) ~ ±[-(moc2)+ (ћ)2(∇ + iq/ћa)2/2mo ]
(i ћ)( ∂t ) + (i2)(qφ ) ~ ±[-(moc2)+ (ћ)2(∇ + iq/ћa)2/2mo ]
(i ћ)( ∂t ) -(qφ ) ~ ±[-(moc2) +(ћ)2(∇ + iq/ћa )2/2mo]
(i ћ)( ∂t ) ~ (qφ )±[-(moc2)+ (ћ)2(∇ + iq/ћa)2/2mo ]
take the negative root
(i ћ)( ∂t ) ~ (qφ ) + [(moc2)- (ћ)2(∇ + iq/ћa)2/2mo ]
(i ћ)( ∂t ) ~ (qφ ) + (moc2)- (ћ)2(∇ + iq/ћa)2/2mo
call (qφ ) + (moc2) = V[x]
(i ћ)( ∂t ) ~ V[x] - (ћ)2(∇ +iq/ћa )2/2mo
typically the vector potential is zero in most non-relativistic settings
(i ћ)( ∂t ) ~ V[x] - (ћ)2(∇)2/2mo
And there you have it, the Schrödinger Equation with a potential
The assumptions for non-relativistic equation were:
Conservative field A, then∂·A = 0
(∇ +a' )2/ i2(M)2 = (∇ +a' )2/ i2(moc/ћ)2 = (ћ)2(∇ +a' )2/i2(moc)2 is near zero
i.e. (ћ)2(∇ +a')2 << (moc)2, a good approximation for low-energy systems
Arbitrarily chose vector potential a = 0
Or keep it around for a near-Pauli equation (we would just have to track spins, not included in this derivation)
Note that the free particle solution∂·∂ = -(moc/ћ)2is shown to be a limiting case for AEM = 0.
Again, see the 4-Vectors Reference for more on this.
Now, let's examine something interesting...
∂·∂ = -(moc / ћ)2: Klein-Gordon Relativistic Wave eqn.
∂ = -i/ћP
∂·(-i/ћP) = -(moc/ ћ)2
∂·(P) = - i (moc)2/ ћ
∂·(P) = 0 - i (moc)2/ ћ
but,∂·(P) = Re[∂·(P)], by definition, since the4-Divergence of any 4-Vector (even a Complex-valued one) must be Real
so∂·(P) = 0 : The conservation of 4-Momentum (i.e. energy&momentum) for our Klein-Gordon relativistic particle.
This is also the equation of continuity which leads to the probability interpretation in the Newtonian limit.
So, the following assumptions within SR-Special Relativity lead toQM-Quantum Mechanics:
| R = (ct,r) |
Location of an event (i.e. a particle)within spacetime |
| U = dR/dτ |
Velocity of the event is the derivative of position with respect to Proper Time |
| P = moU |
Momentum is just the Rest Mass of the particle times its velocity |
| K = P /ћ |
A particle's wave vector is just the momentum divided by Planck's constant, but uncertain by a phase factor |
| ∂ = -iK |
The change in spacetime corresponds to(-i) times the wave vector, whatever that means... |
| D = ∂ + (iq/ћ)A |
The particle with minimal coupling interaction in a potential field |
Each relation may seem simple, but there is a lot of complexity generated by each level.
It can be shown that the Klein-Gordon equation describes a non-local wave function, which "violates relativistic causality when used to describe particles localized to within more than a Compton wavelength,..."-Baym. The non-locality problem in QM is also the root of the EPR paradox. I suspect that all of these locality problems are generated by the last equation, where the factor of ( i ) is loaded into the works, although it could be at the wave-particle duality equation. Or perhaps we are just not interpreting the equations correctly since we derived everything from SR, which should obey its own relativistic causality.
Let's examine the last relation on a quantum wave ket vector | V ⟩:
∂ = -iK
∂ | V ⟩ = -iK | V ⟩ which gives time eqn .[∂/c∂t | V ⟩ = -iω/c | V ⟩] and space eqn. [-∇ | V ⟩ = -ik | V ⟩]
A solution to this equation is:
| V ⟩ = vn e^(-iKn·R) | Vn ⟩ where vn is a real number, | Vn ⟩ is an eigenstate(stationary state)
Generally, | V ⟩ can be a superposition of eigenstates | Vn ⟩
N
| V ⟩ = Sum [vn e^(-iKn·R) | Vn ⟩]
n = 1
Going back to the 4-wave vector K, I believe that this is the part of the derivation of QM from SR that the quantum probabilistic interpretation becomes necessary. Since the 4-wave vector as given here does not define the phase relationship, there is some ambiguity or uncertainty in the description. Phase almost certainly plays some role. Again, presumably 2*Pi of 4-wave vectors could describe the same 4-momentum vector. Once one starts taking waves to be the primary description of a system, the particle aspect gets lost, or smeared out. Once the gradient operation is added to the mix, one gets what is essentially a diffusion equation for waves, in which the particle aspect is lost. Thus, a probabilistic interpretation is needed, showing that the particle is located somewhere/when in the spacetime, but can't quite be pinned down exactly. My bet is that if the phases could be found, the exact locations of particle events would ari
se.
========================
This remains a work in progress.
Thesis by John B. Wilson
Reference papers/books can be found in the see 4-Vectors & Lorentz Scalars Reference.
Email me, especially if you notice errors (which I will fix ASAP) or have interesting comments.
Please, send comments to John Wilson

quantum
relativity

See SRQM: QM from SR - The 4-Vector RoadMap (.html)
See SRQM: QM from SR - The 4-Vector RoadMap (.pdf)
SRQM Physics Diagramming Method

SRQM 4-Vector : Four-Vector and Lorentz Scalar Diagram
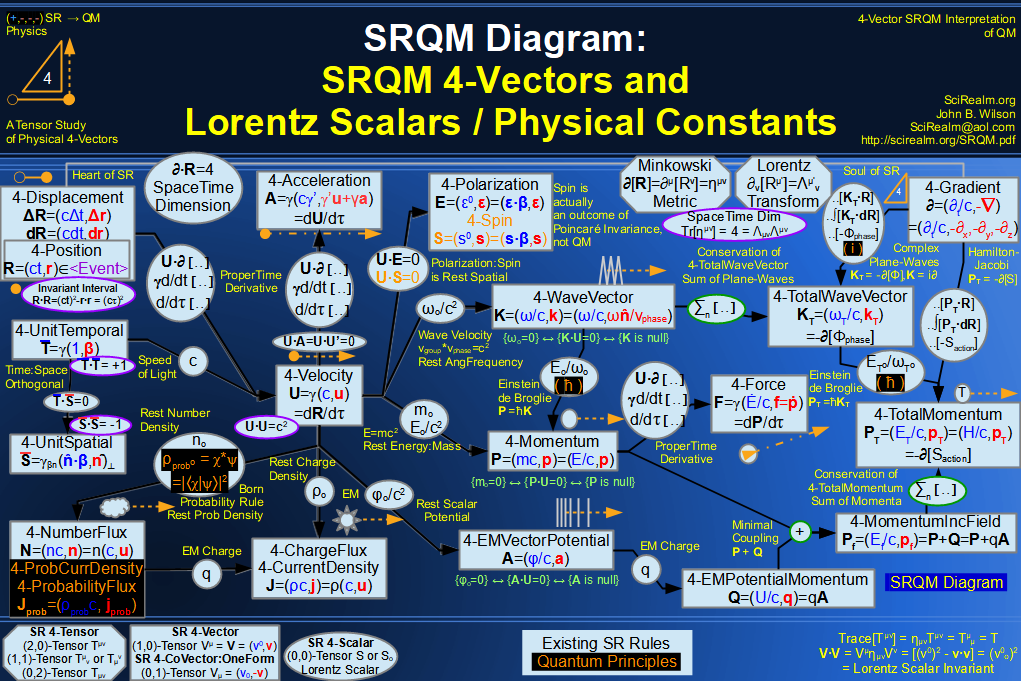
SRQM + EM 4-Vector : Four-Vector and Lorentz Scalar Diagram
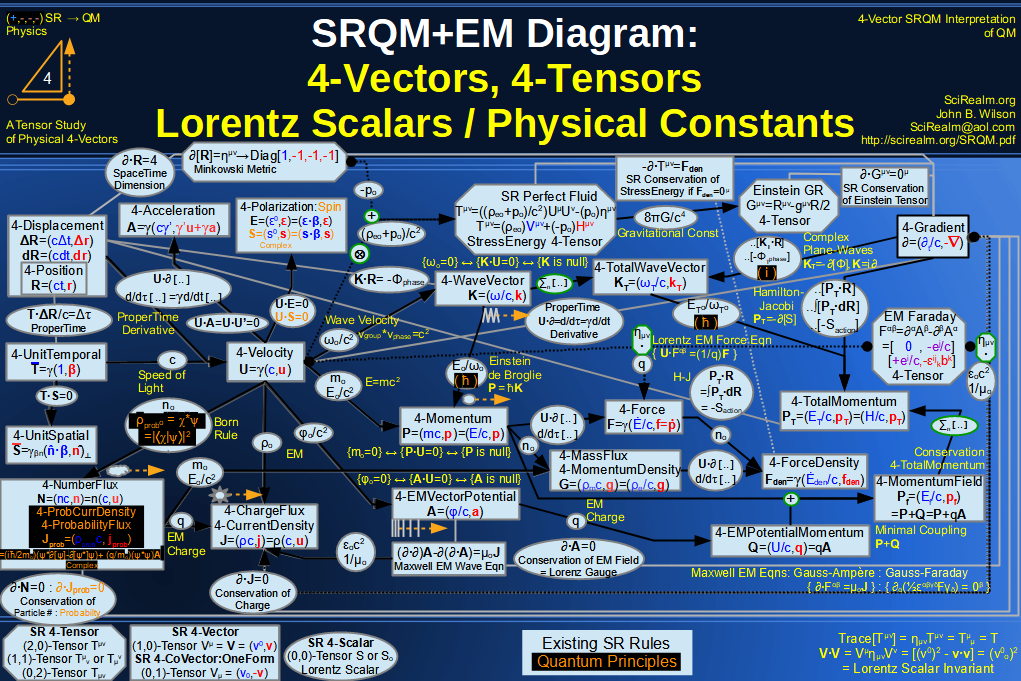
SRQM + EM 4-Vector : Four-Vector and Lorentz Scalar Diagram With Tensor Invariants
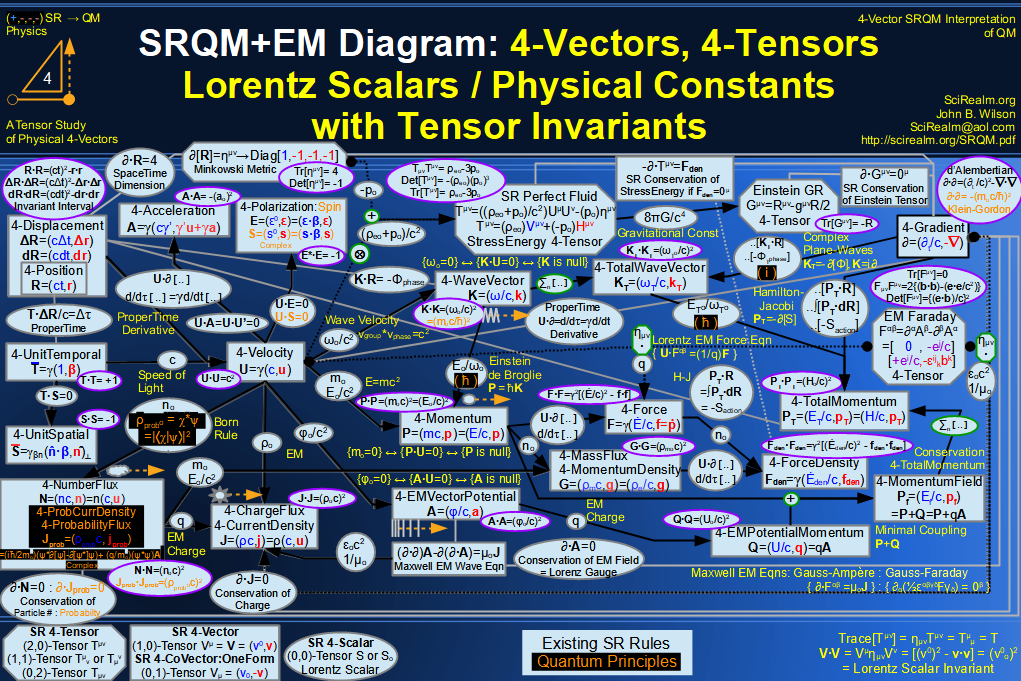
SRQM 4-Vector : Four-Vector Stress-Energy & Projection Tensors Diagram
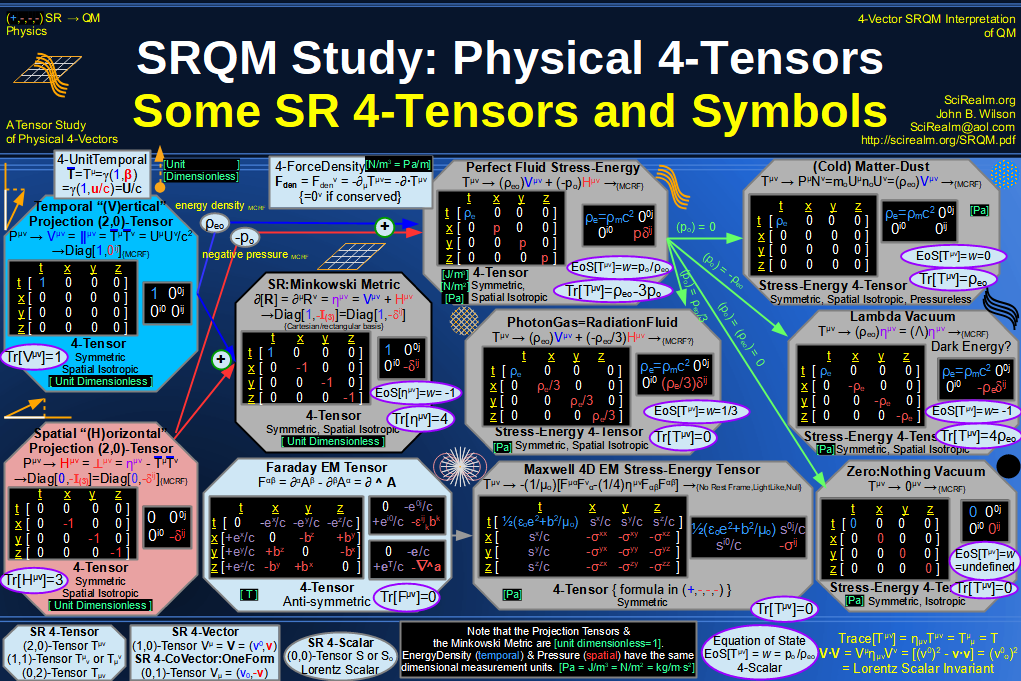
SRQM 4-Vector : Four-Vector SR Quantum RoadMap
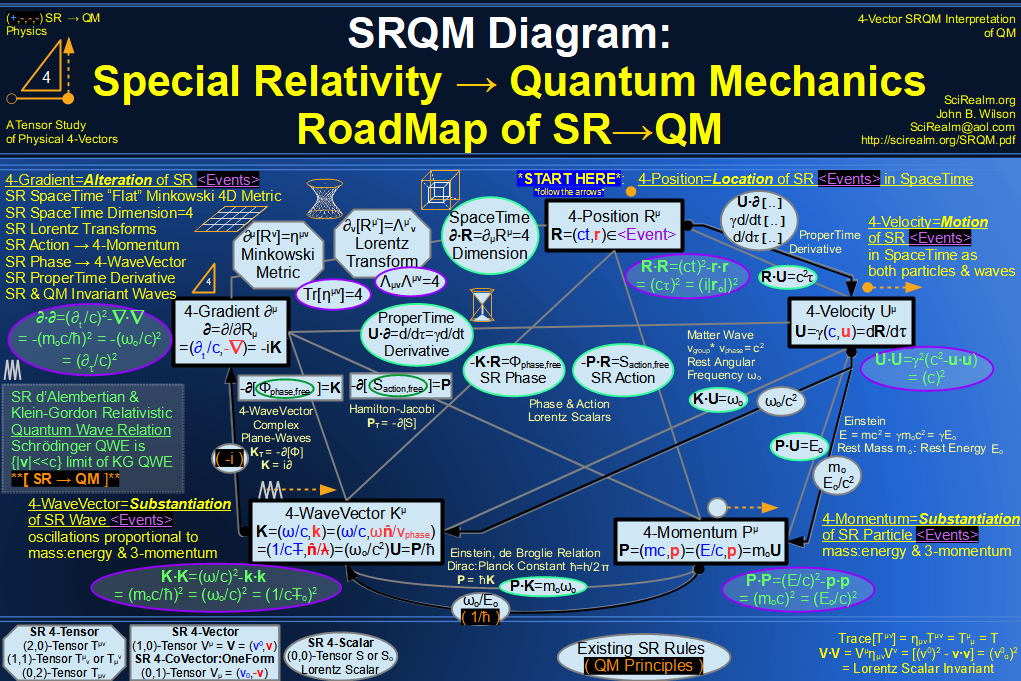
SRQM + EM 4-Vector : Four-Vector SR Quantum RoadMap
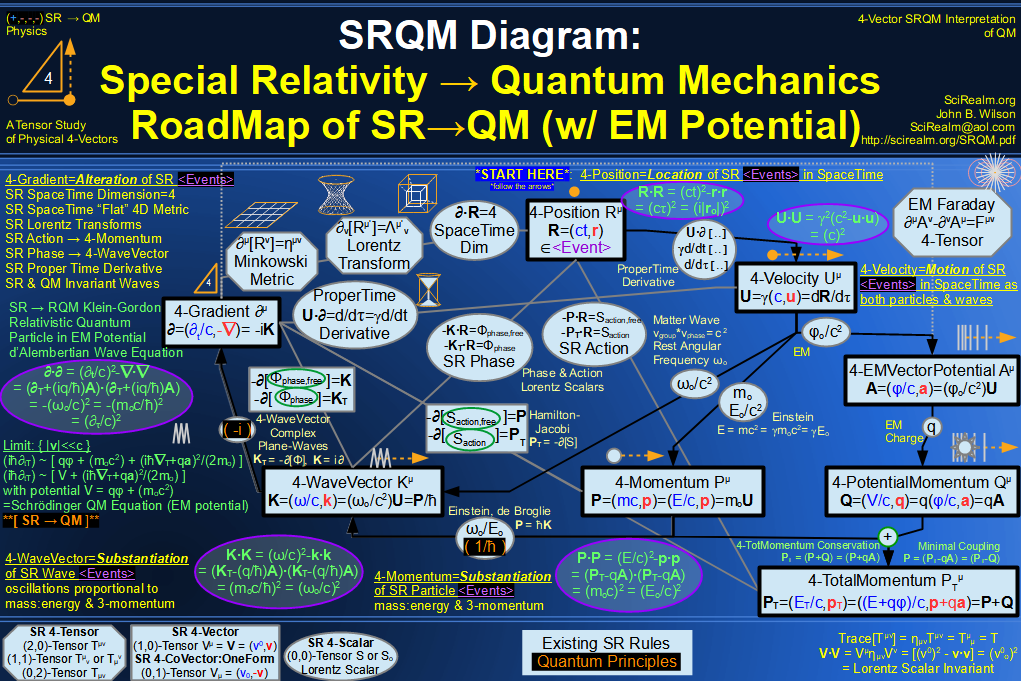
SRQM + EM 4-Vector : Four-Vector SR Quantum RoadMap - Simple

SRQM 4-Vector : Four-Vector New Relativistic Quantum Paradigm
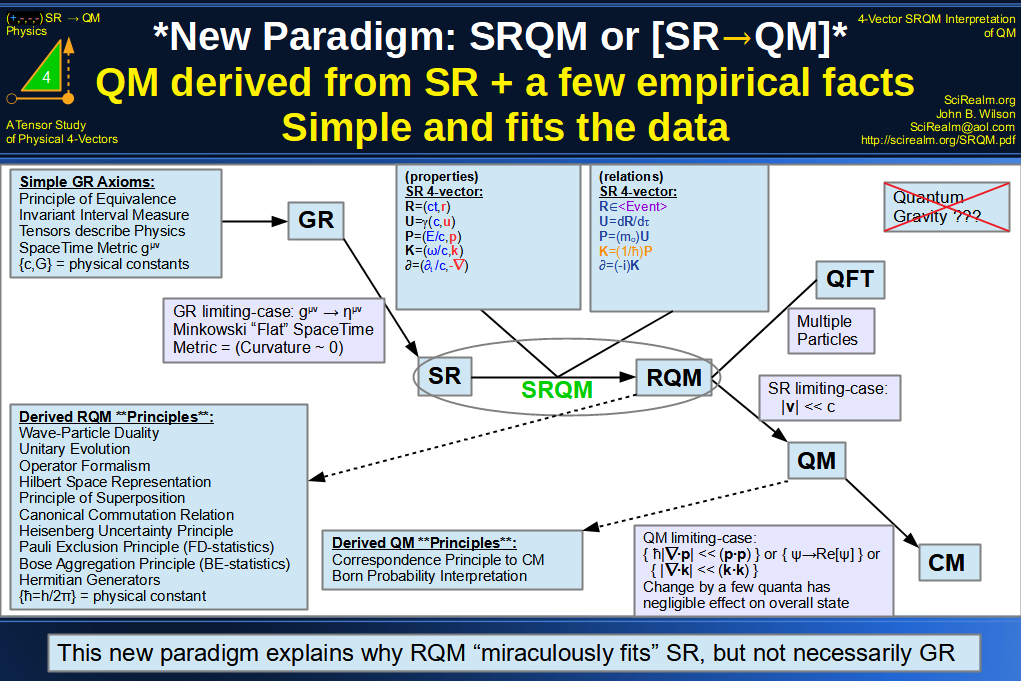
SRQM + EM 4-Vector : Four-Vector New Relativistic Quantum Paradigm (with EM)
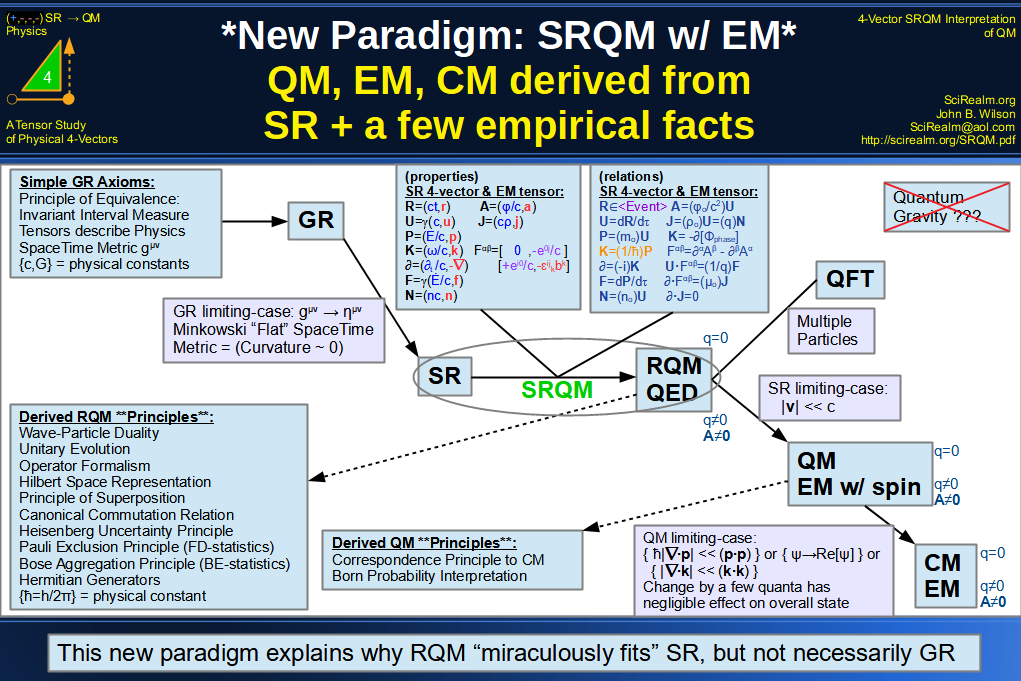
SRQM 4-Vector : Four-Vector New Relativistic Quantum Paradigm - Venn Diagram

SRQM 4-Vector : Four-Vector SpaceTime is 4D

SRQM 4-Vector : Four-Vector SpaceTime Orthogonality
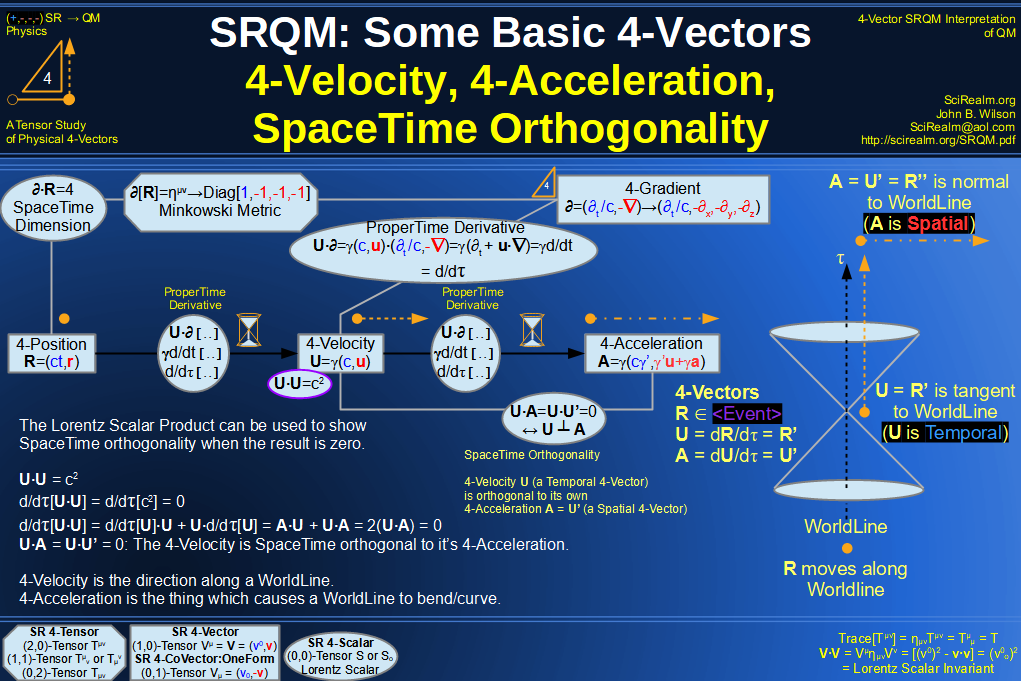
SRQM 4-Vector : Four-Vector 4-Position, 4-Velocity, 4-Acceleration Diagram

SRQM 4-Vector : Four-Vector 4-Displacement, 4-Velocity, Relativity of Simultaneity Diagram

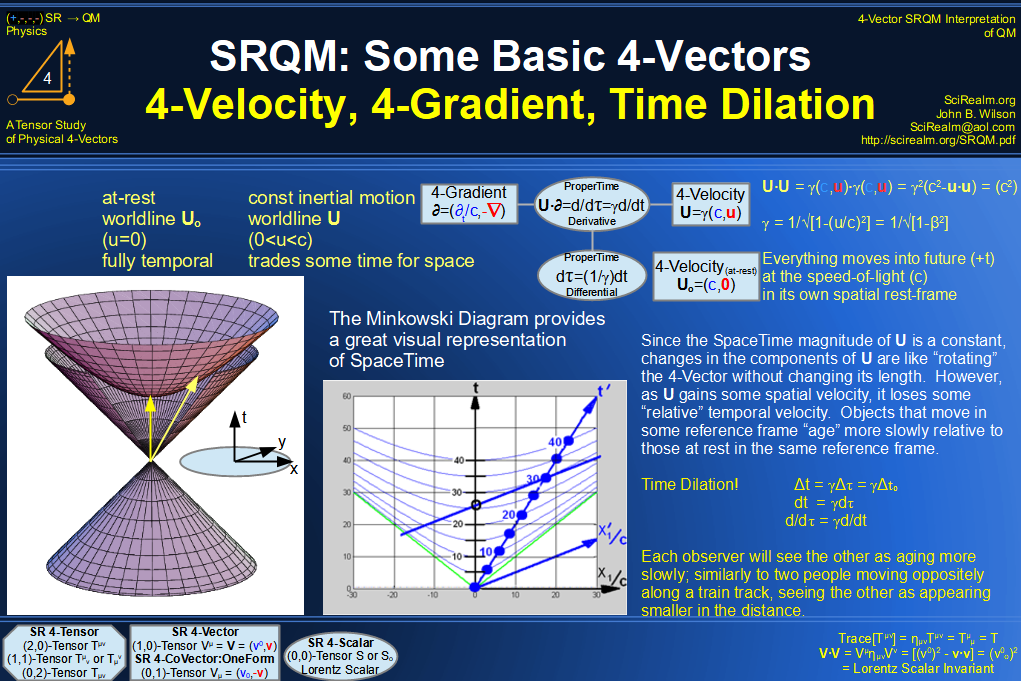
SRQM 4-Vector : Four-Vector 4-Velocity, 4-Gradient, Time Dilation Diagram
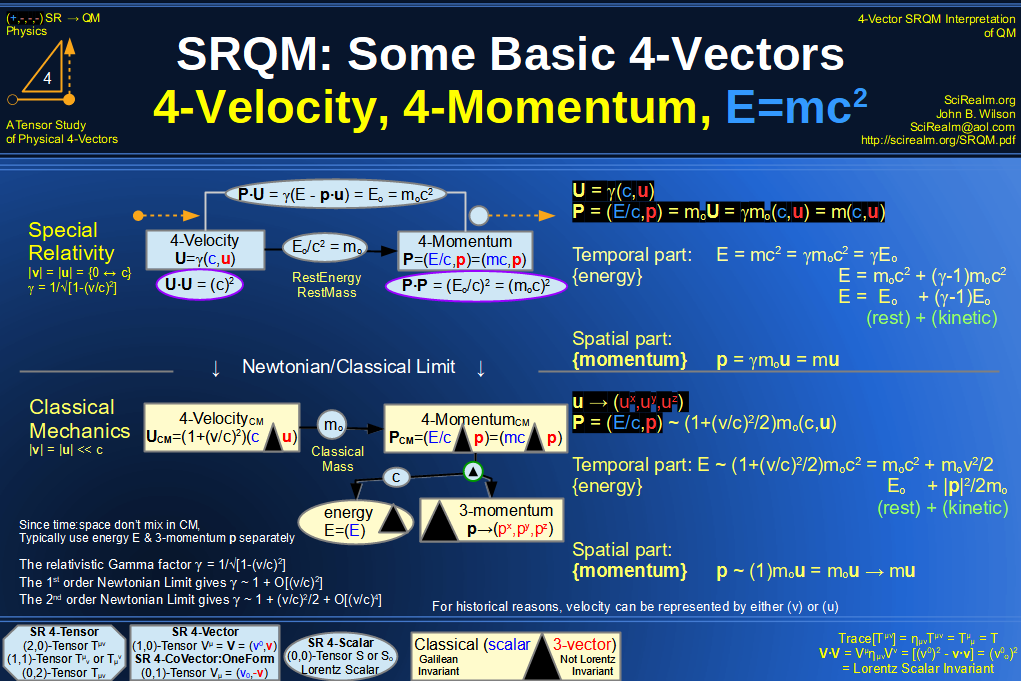
SRQM 4-Vector : Four-Vector 4-Vector, 4-Velocity, 4-Momentum, E=mc^2 Diagram
SRQM 4-Vector : Four-Vector 4-Velocity, 4-WaveVector, Relativistic Doppler Effect Diagram

SRQM 4-Vector : Four-Vector Wave-Particle Diagram
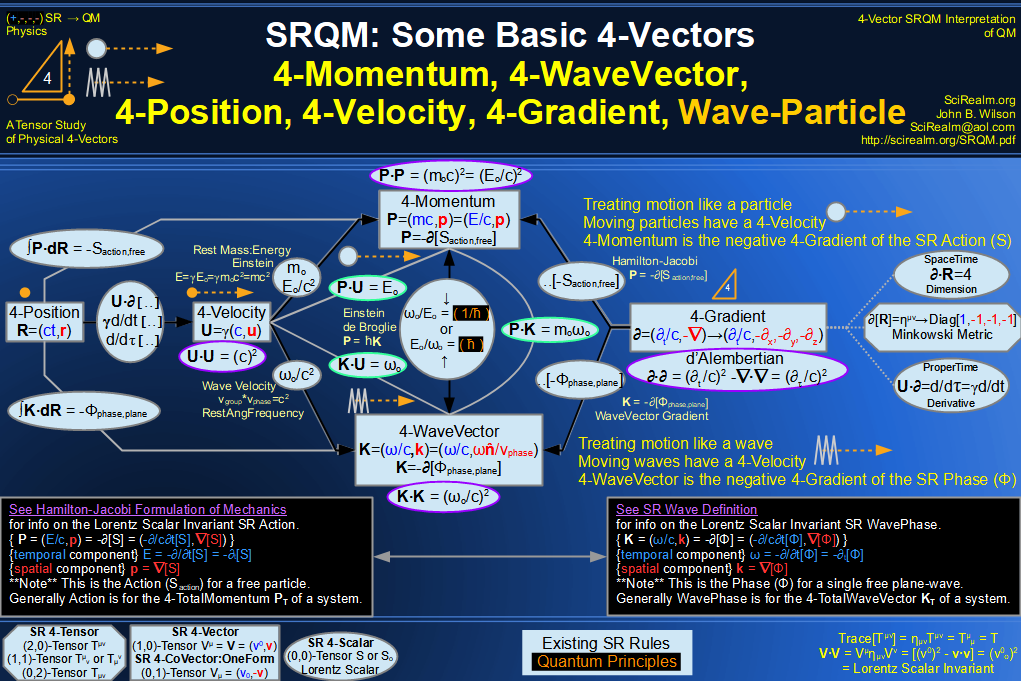
SRQM 4-Vector : Four-Vector Compton Effect Diagram
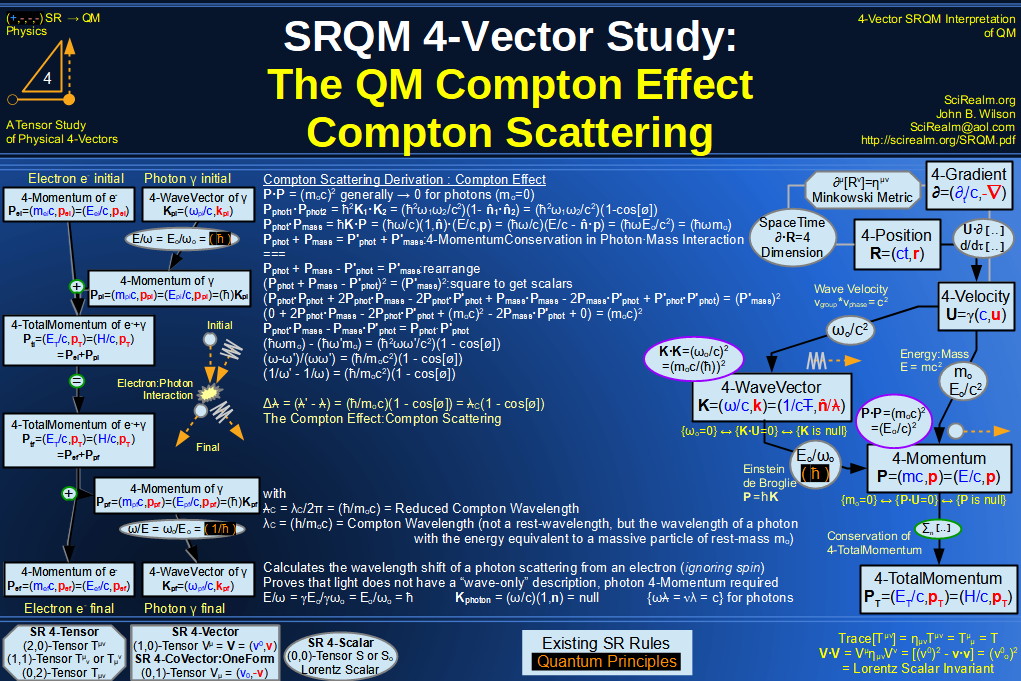
SRQM 4-Vector : Four-Vector Aharonov-Bohm Effect Diagram
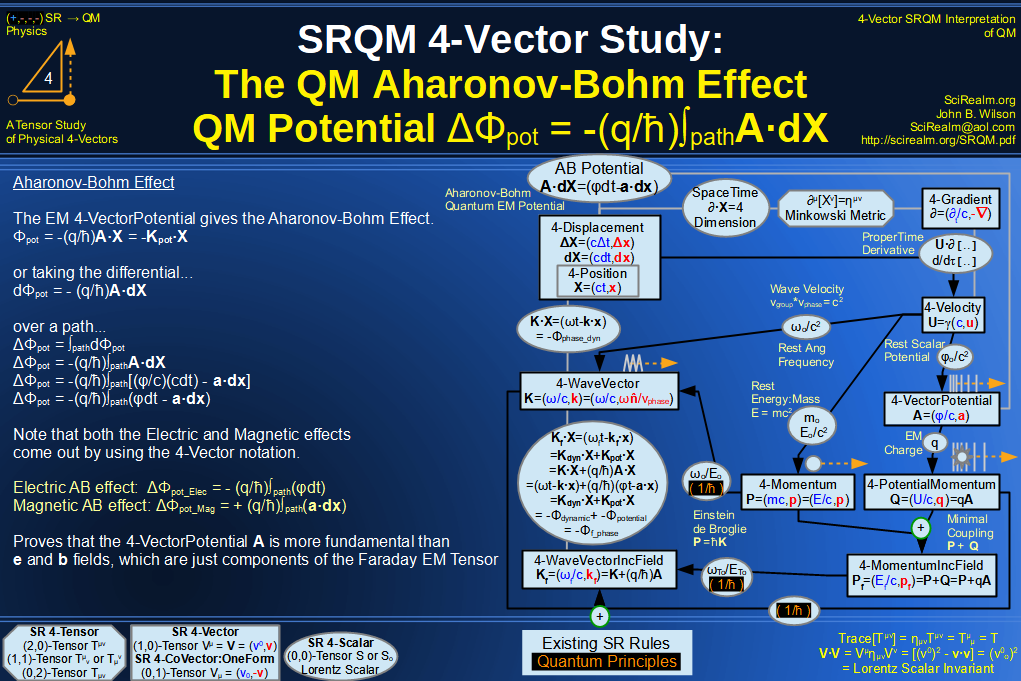
SRQM 4-Vector : Four-Vector Josephson Junction Effect Diagram
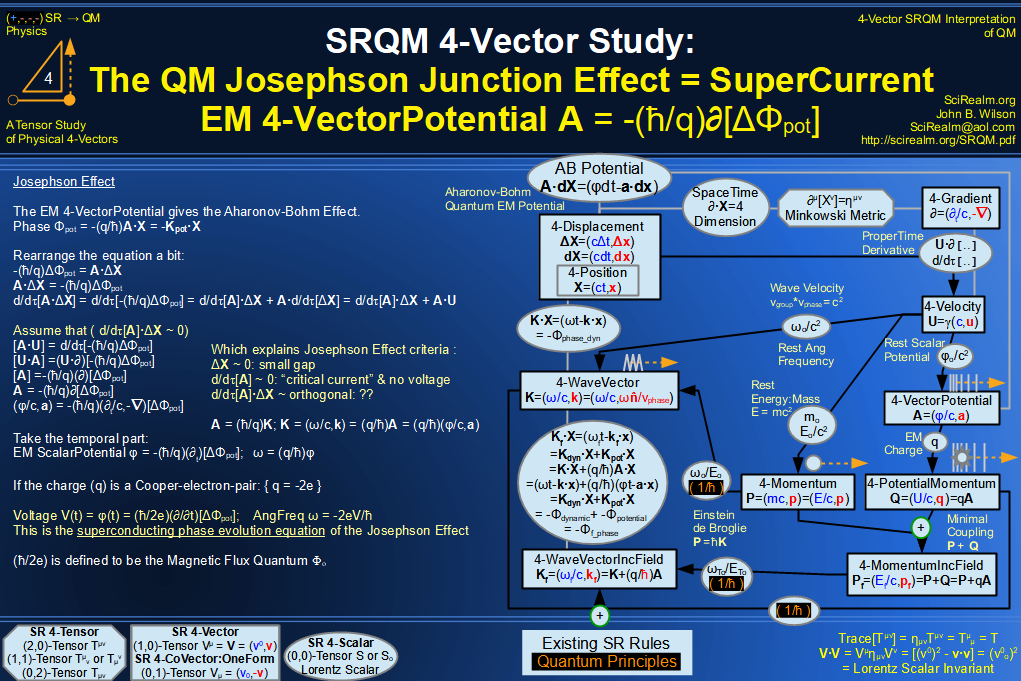
SRQM 4-Vector : Four-Vector Hamilton-Jacobi vs Action, Josephson vs Aharonov-Bohm Diagram
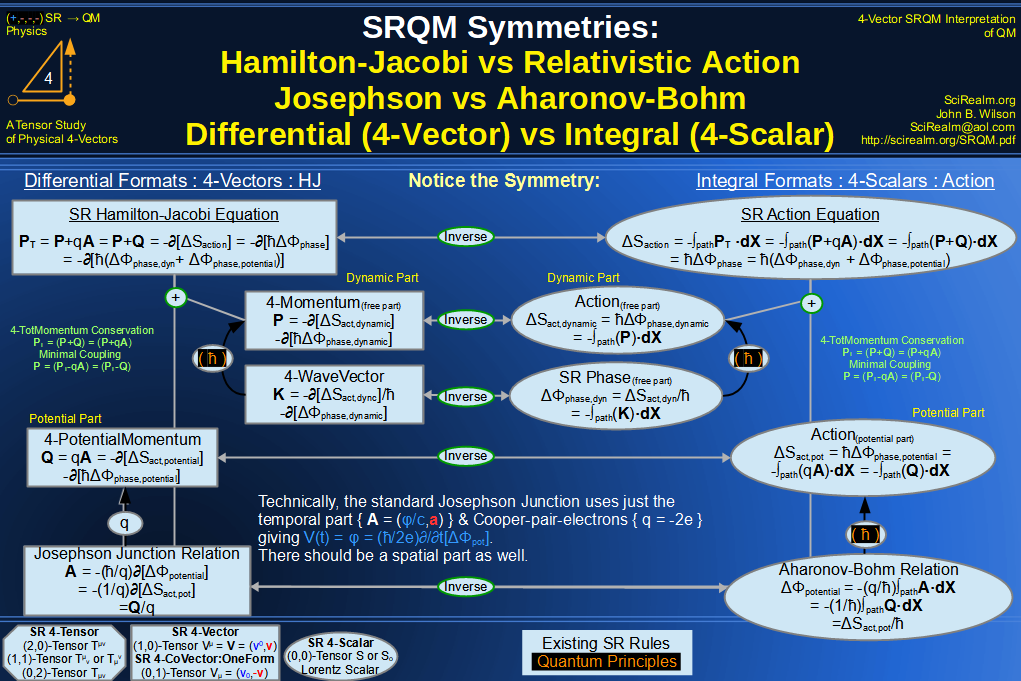
SRQM 4-Vector : Four-Vector Motion of Lorentz Scalar Invariants
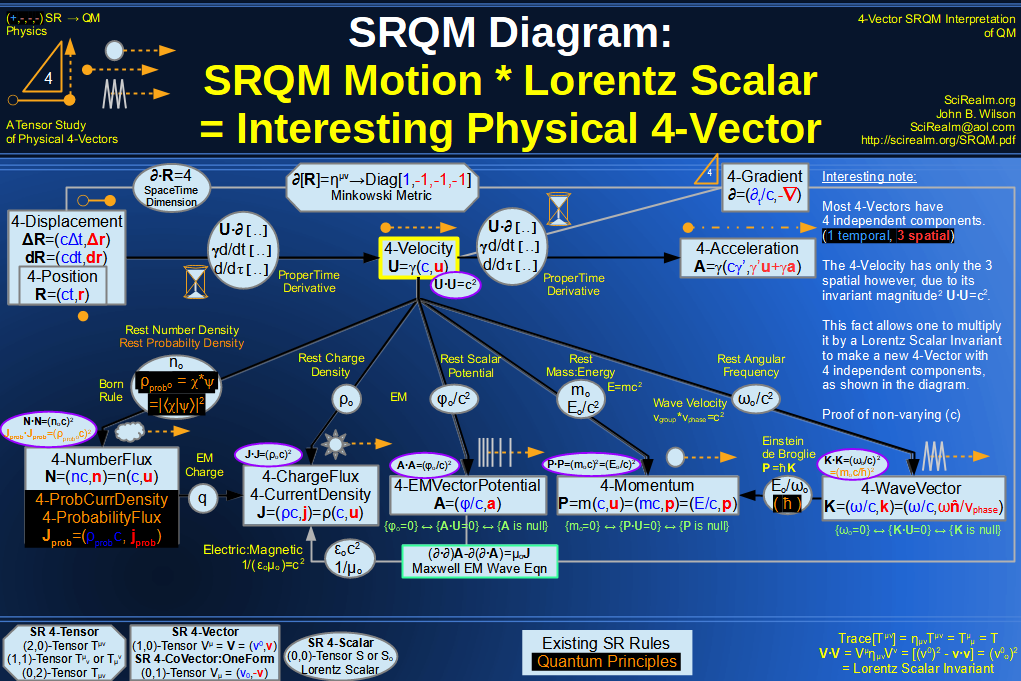
SRQM 4-Vector : Four-Vector Motion of Lorentz Scalar Invariants, Conservation Laws & Continuity Equations
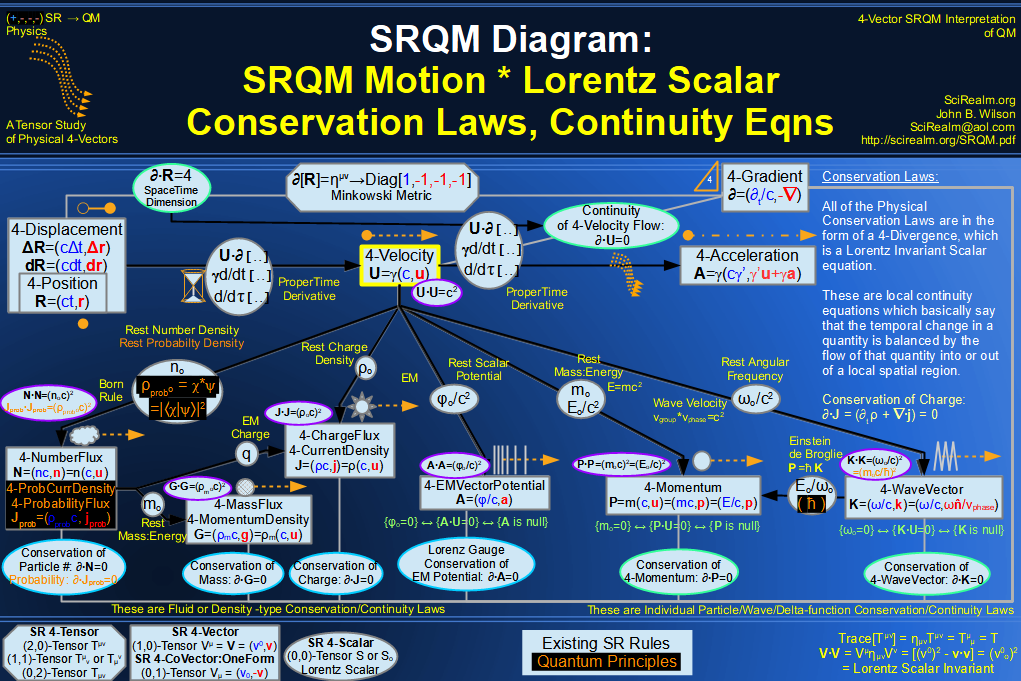
SRQM 4-Vector : Four-Vector Speed of Light (c)
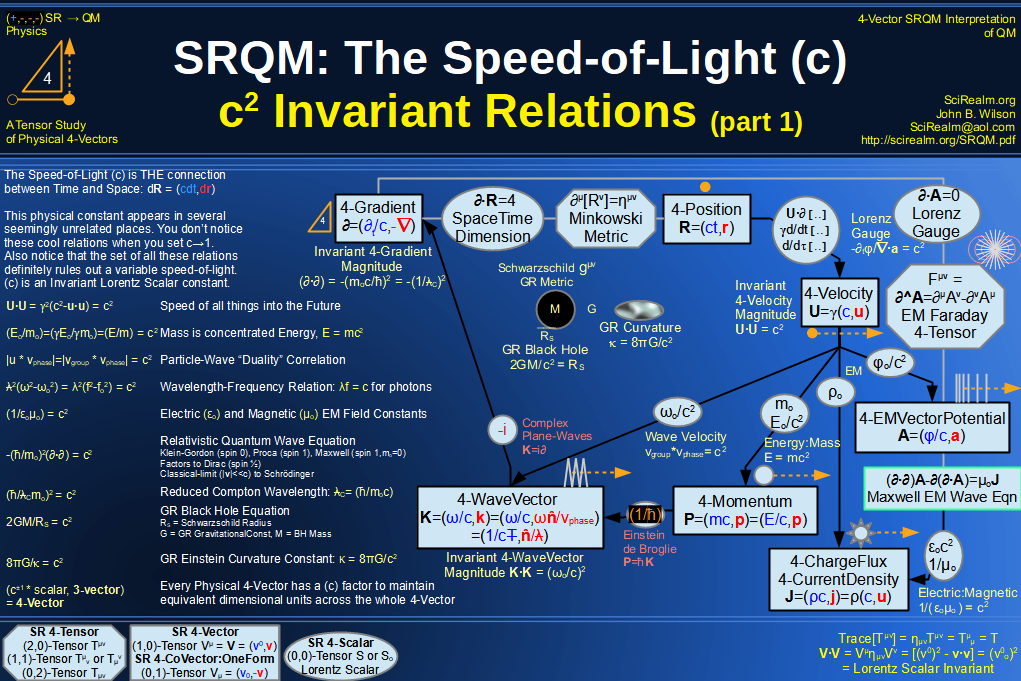
SRQM 4-Vector : Four-Vector Minimal Coupling Conservation of 4-TotalMomentum)
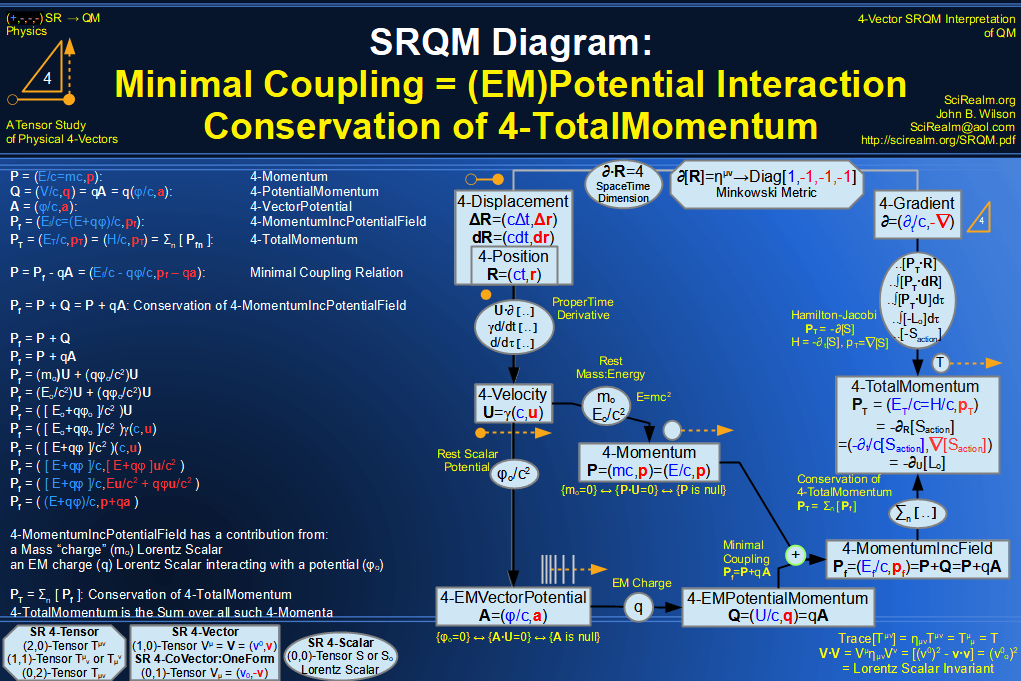
SRQM 4-Vector : Four-Vector Relativistic Action (S) Diagram
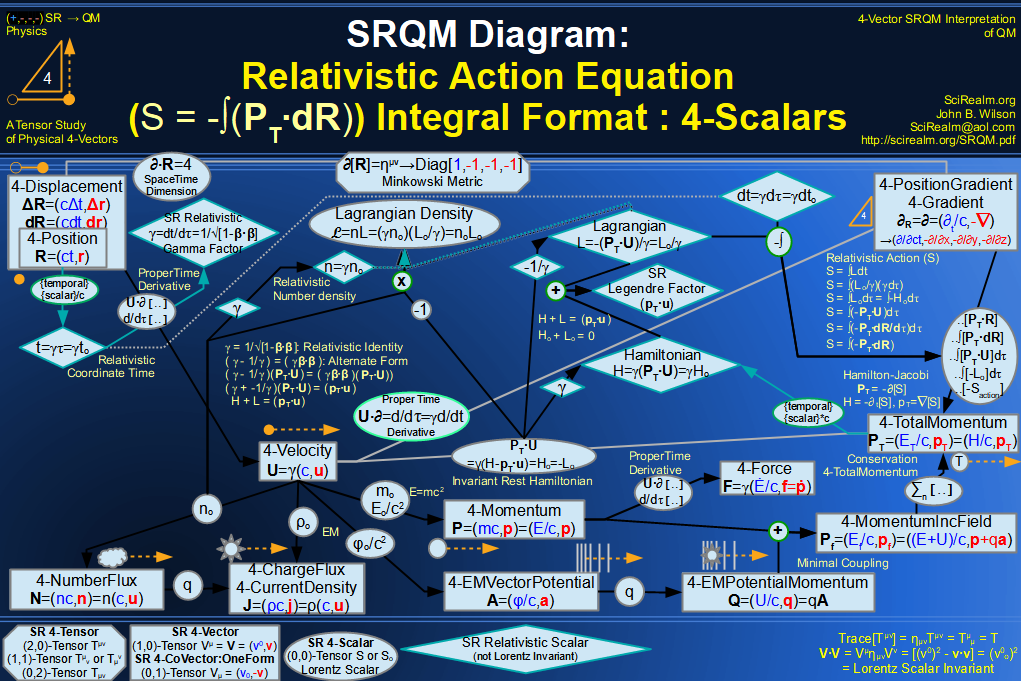
SRQM 4-Vector : Four-Vector Relativistic Lagrangian Hamiltonian Diagram
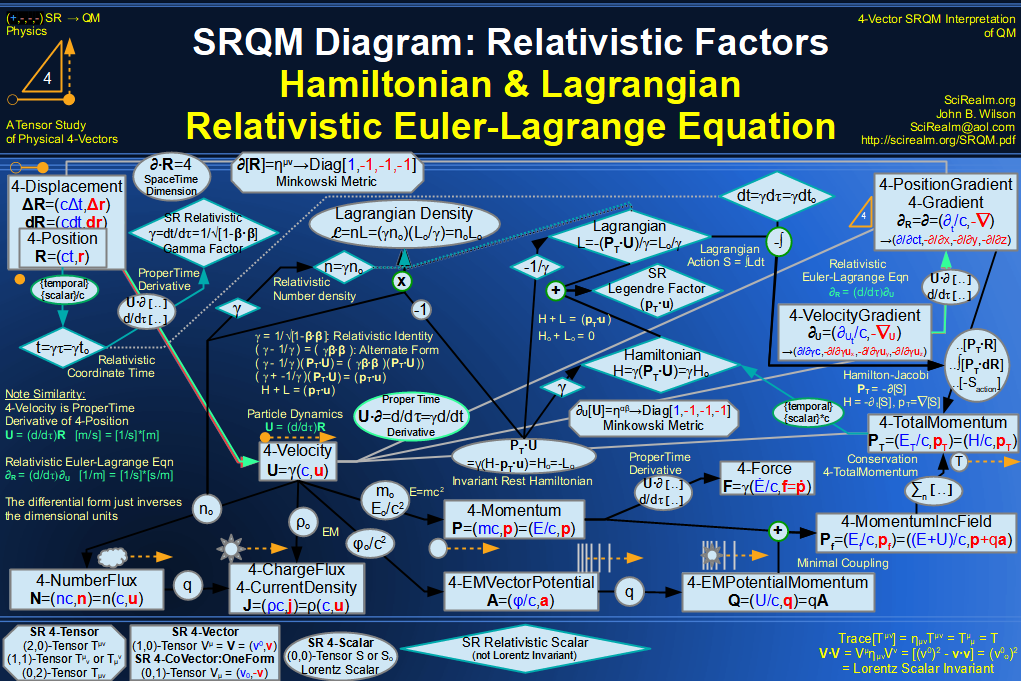
SRQM 4-Vector : Four-Vector Relativistic Euler-Lagrange Equation
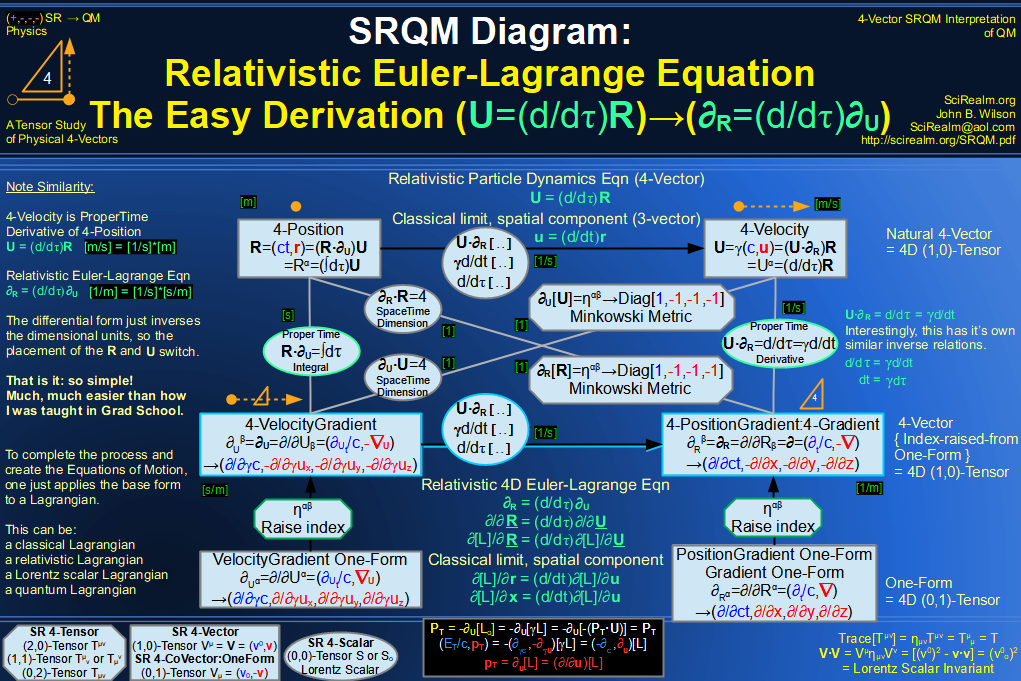
SRQM 4-Vector : Four-Vector Relativistic EM Equations of Motion

SRQM 4-Vector : Four-Vector Einstein-de Broglie Relation hbar
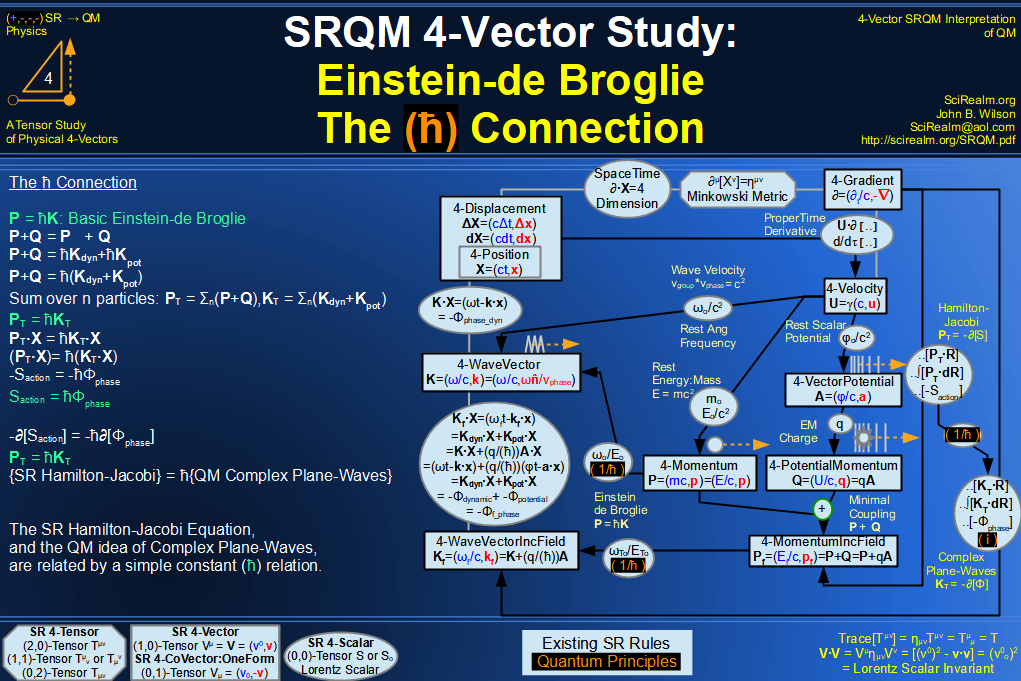
SRQM 4-Vector : Four-Vector Quantum Canonical Commutation Relation
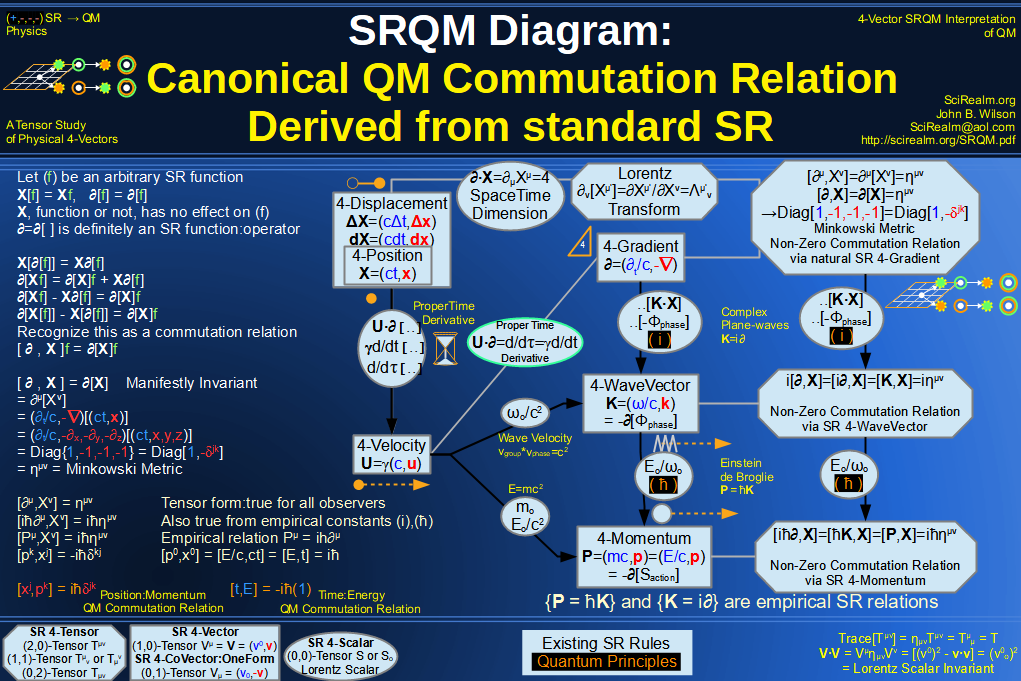
SRQM 4-Vector : Four-Vector QM Schroedinger Relation
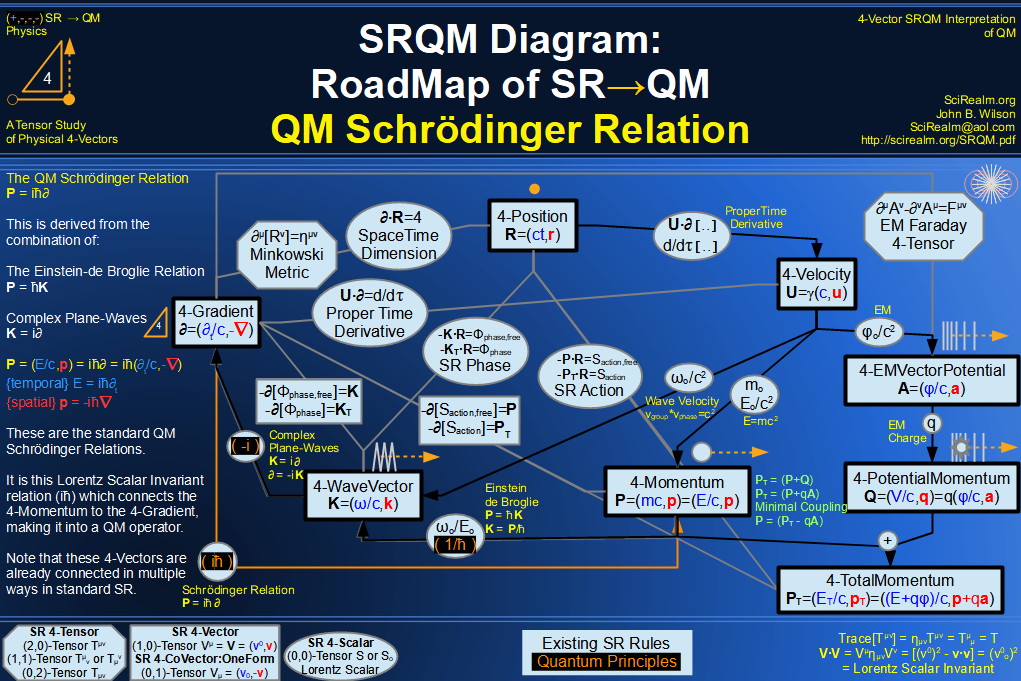
SRQM 4-Vector : Four-Vector Quantum Probability
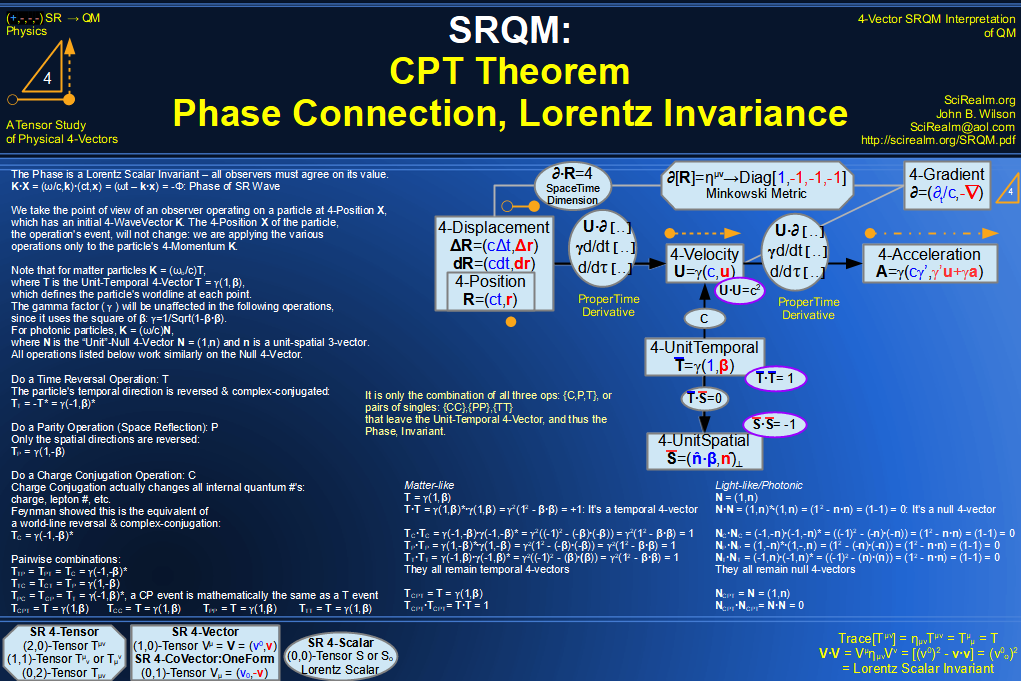
SRQM 4-Vector : Four-Vector CPT Theorem
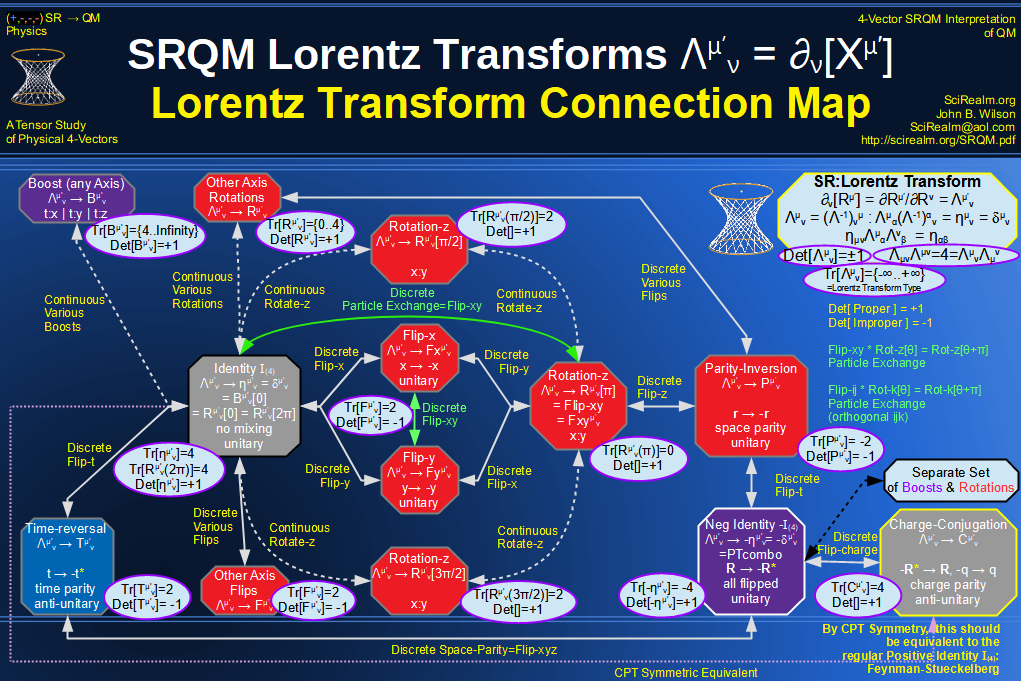
SRQM 4-Vector : Four-Vector Lorentz Transforms Connection Map
SRQM 4-Vector : Four-Vector Lorentz Discrete Transforms

SRQM 4-Vector : Four-Vector Lorentz Transforms - Trace Identification

SRQM 4-Vector : Four-Vector Lorentz Lorentz Transforms-Interpretations
CPT Symmetry, Baryon Asymmetry Problem Solution, Matter-Antimatter Symmetry Solution, Arrow-of-Time Problem Solution, Big-Bang!

See SRQM: QM from SR - The 4-Vector RoadMap (.html)
See SRQM: QM from SR - The 4-Vector RoadMap (.pdf)